§7. Разложение функций в степенной ряд. Ряд Тейлора.

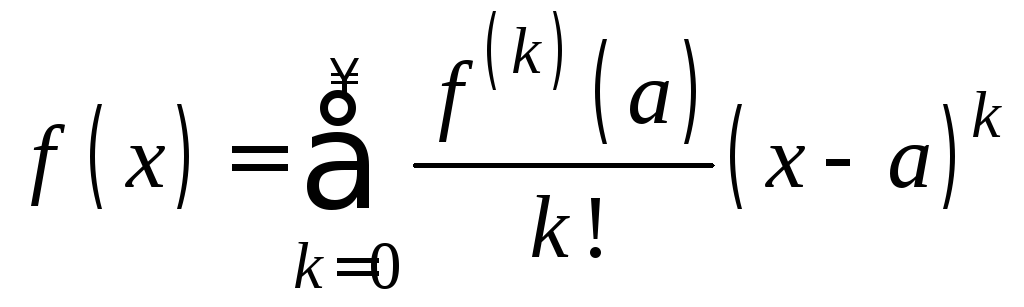Теорема о единственности степенного разложения. Если, тои, следовательно,(ряд Тейлора).

Доказательство. Повторно дифференцируя исходное тождество, получаем

.. Поэтому. Ч и т.д.

Как мы уже знаем, для представимости функции в виде суммы степенного ряда на интервале необходимо, чтобы эта функция была там бесконечно дифференцируемой. Это условие, однако, не является достаточным.

Контрпример. Пусть. Нетрудно доказать, что, в частности,. В то же время,невозможно представить в виде, иначе было бы, что неверно, так как.

Сформулируем теперь достаточное условие представимости функции рядом Тейлора. Введём для этого величины .

Теорема. Если последовательность чиселограничена, то

на отрезке .

Пользуясь этой теоремой и конечной формулой Тейлора для функций и, получаем разложения в ряд Тейлора этих функций на всей числовой оси:

1) ; 2);3);

4) ; 5).

Немного сложнее обосновать разложения:

6) ; 7);

8) .

В последнем разложении используется обозначение .

§8. Некоторые приложения степенных рядов.

Пример 1.Вычислить суммы рядов (ряд Лейбница) и.

Решение. Если подставитьв обе части разложений 6) и 7), то сразу же получим

.

Дополнение. Ряды из примера 1 непригодны для вычислений, они слишком медленно сходятся. Так, остатокрядаубывает со скоростьюи для вычисления с точностьюнеобходимо просуммировать 1000 членов ряда. Покажем на том же примере, что метод степенных рядов может давать отличные результаты, если алгоритм вычислений немного усовершенствовать. Снова обратимся к табличному разложению 6). Это даёт

,

.

Следовательно, . Заменаприводит к тождеству. Здесьи если, то.

Поэтому . Этот ряд сходится гораздо быстрее.

Сейчас .

В частности, , а потому с точностьюбудет. Отбрасывая ненадёжные знаки, получаем. Для уменьшения погрешности вычислений нужно увеличить количество учитываемых членов ряда. Так, например,, поэтомус точностью.

Пример 2. Вычислить с точностьюинтеграл.

Решение. Так как, то.

Поэтому =.

По теореме Лейбница , то. Округляя, получаем с нужной точностью.

Пример 3. Найти приближенное решение уравнениявблизи.

Решение. Ясно, что.

Дифференцируя данное уравнение, получаем новое тождество: .

это даётили.

Повторим это рассуждение еще несколько раз. Это даёт:

, или.

,или.

При желании можно было бы продолжать эти вычисления.

Если использовать найденные значения для построения начального отрезка ряда Тейлора, то приходим к приближенному выражению для функциив окрестности точки: .На следующем рисунке сравниваются график полученного приближенного решенияс графиком точного решения.

§9. Тригонометрические ряды Фурье.

1˚. Для понимания некоторых вопросов анализа целесообразно использование геометрической терминологии. Так, в математическом анализе приходится раскладывать функции по ортогональному базису. Подробнее об этом.

Напомним, что скалярное произведениев абстрактном линейном пространстве вводилось с помощью системы аксиом:

1. функция являетсябилинейной формой, т.е.линейнаи;

2. функция симметрична, т. е.;

3. функция являетсяположительно определённой, т.е.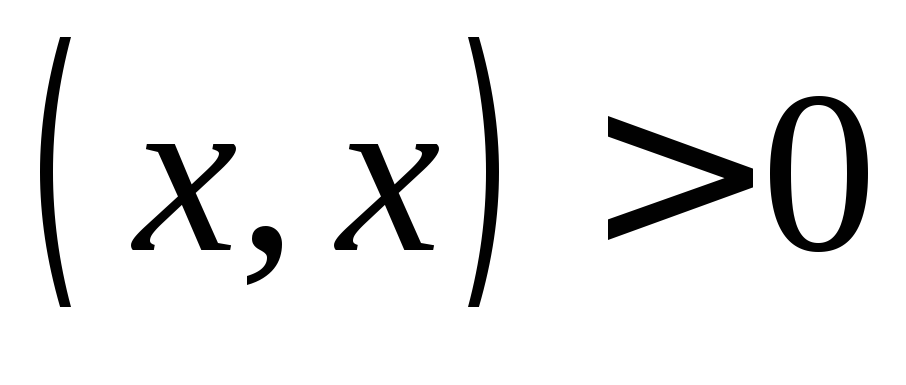, если.

Например, в пространстве скалярным произведением является выражение.

Векторы иназываютсяортогональными,если. Набор ненулевых векторовобразуетортогональную систему, если все они попарно ортогональны.

Предположим теперь, что вектор требуется разложить по ортогональной системе, т.е. представить в виде. Спрашивается, чему равны коэффициенты разложения? Если умножить обе части разложения скалярно на один из векторов системы, например,, получимили. Коэффициенты, вычисляемые по этой формуле, часто называюткоэффициентами Фурье. Напомним ещё, что для ортогонального разложения справедлив следующий вариант теоремы Пифагора:.

2˚. В математическом анализе, в отличие от линейной алгебры, обычно приходится иметь дело с бесконечномерными пространствами. Но и здесь можно говорить о скалярном произведении, ортогональных системах, коэффициентах Фурье. Так, в линейном пространствечасто рассматривают интегральное скалярное произведение:(интеграл − вместо суммы). Ясно, что и здесь выполнены все аксиомы скалярного произведения.

Лемма. Классическая тригонометрическая системаявляется ортогональной относительно введенного только что скалярного произведения. Скалярный квадрат функции, очевидно, равен, скалярный квадрат любой другой функции системы равен.

Доказательство. Прежде всего, ясно, что любая изсистемы ортогональна любой, в том числе − функции. Вычислим скалярные произведения одноимённых функций. Мы имеем:

Из доказанной леммы и формулы для коэффициентов Фурье следует, что разложение по тригонометрической системе для функции имеет вид:

, где,.

Ряд называется рядом Фурье функции. Символвместо ожидаемого знака равенства означает только то, что справа от него стоит ряд Фурье, т.е. не предполагается, что этот ряд сходится и, тем более, − что его суммасовпадаёт с.

Приведём без доказательства достаточные условия представимости функции её рядом Фурье.

Теорема 1. Пусть−функция, кусочно-гладкая на периоде. В таком случае ряд Фурье сходится при любом, а его суммаравна. В частности, если− точка непрерывности, то.

Теорема 2. Если в дополнение к условиям теоремы 1.− непрерывна, то её ряд Фурьеправильносходится, то есть мажорируется сходящимся числовым рядом.

Замечание. Мы видим, что технически ряды Фурье сложнее степенных рядов, зато область применения рядов Фурье гораздо шире. Так, в ряд Тейлора можно разложить далеко не всякую бесконечно дифференцируемую функцию, в то время как в ряд Фурье раскладываются многие разрывные функции.

Теорема Пифагора в этом случае приобретает вид

(равенство Парсеваля - Стеклова).

Если − четная функция, то, очевидно,. Если же− нечетная функция, то.