Глава 2. Производная. §1.Задачи, приводящие к понятию производной. Определение.

1⁰. Задача о скорости движения. Точка движется прямолинейно так, что в любой момент времениона находится на расстоянииот начального положения. Найти мгновенную скорость точки в момент времени.

За время пройденный путь изменился на величину. Средняя скорость движения за этот промежуток времени равна, Мгновенной скоростьюв момент времениназывается предел этого отношения при условии, что. Поэтому.

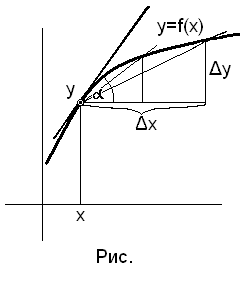
20. Задача о касательной. Найти угловой коэффициенткасательной к графику функции. Касательная это − предельное положение секущей, проходящей через две точки кривой, одна из которых зафиксирована, а другая неограниченно к ней приближается. Т.к. угловой коэффициент секущей равен (см. Рис.), то

Подобную конструкцию приходится использовать и при решении задачи о скорости химической реакции, задачи о плотности материала или плотности заряда стержня, о температурном градиенте и др. Это приводит к необходимости принять следующее общее определение.

Определение. Производнойфункциив точкеназывается величина, равная пределу (если он существует) отношения приращения функции к вызвавшему его приращению независимой переменной при условии, что это последнее приращение стремится к нулю, т.е.

.

Сформулируем некоторое обобщение этого определения. Может случиться, что существует предел рассмотренного отношения приращений при стремлении к нулю слева, то есть существует. Тогда этот предел называетсялевосторонней производной. Точно так же величинаназываетсяправосторонней производнойфункциив точке.

§2. Свойства дифференцируемых функций.

Определение.Функцияназываетсядифференцируемойв точке, если её приращениеможет быть представлено в виде суммы двух слагаемых, из которых первое пропорционально, а второе − бесконечно малая величина более высокого прядка, т.е., когда. В этом случае главная линейная часть приращения функцииназываетсядифференциалом функции и обозначается, т.е..

Теорема. 1. Функция дифференцируема в точке, тогда и только тогда, когда в этой точке у нее есть производная.

Доказательств.

, где .

Пример. Рассмотрим функцию . Так как, то. Таким образом.

Следствие. Если функция дифференцируема в точке, то.

Теорема. 2. Функция, дифференцируемая в точке , непрерывна в этой точке. Обратное утверждение неверно.

Доказательство. Если ,то . Непрерывность доказана.

Вторая часть следует из контрпримера: функция всюду непрерывна. В то же время,, а, поэтому функция не является дифференцируемой.

§3. Правила дифференцирования.

1. Если существуют производные и , то

.

2. Если существуют производные и , то

.

В частности, если , то.

Упражнение. С помощью ММИ обобщить правила 1. и 2. на случайфункций.

3. Если существуют производные и , причем , то

.

Доказательство правила 3. Так как , то, аналогично,. Поэтомуввиду непрерывностив точке.

Упражнение.Дать словесную формулировку правил 1.−3.

4. (Производная сложной функции). Пусть функциядифференцируема в точке, а функциядифференцируема в точке. В таком случае сложная функциядифференцируема в точке. При этом.

Доказательство. По условиюи. Подставляя это выражениев первое равенство, получаем

.

Этим доказана и дифференцируемость в точкеи формула.

Замечание. Можно считать, что в теореме 4 речь идёт о замене переменной. При этом, но, так как− только главная часть. Таким образом, запись дифференциала в видев отличие от записисохраняется и после замены переменной (инвариантна относительно замены переменной).

5. (Производная обратной функции). Если функциянепрерывна и строго возрастает в окрестности точки, а в самой точкедифференцируема, причём, то обратная функциядифференцируема в точке. При этом(совсем коротко).

Доказательство. Из условия следует, что обе функциинепрерывны и строго возрастают в соответствующих окрестностях, т.е.могут стремиться к нулю (равняться нулю) только одновременно. Поэтому.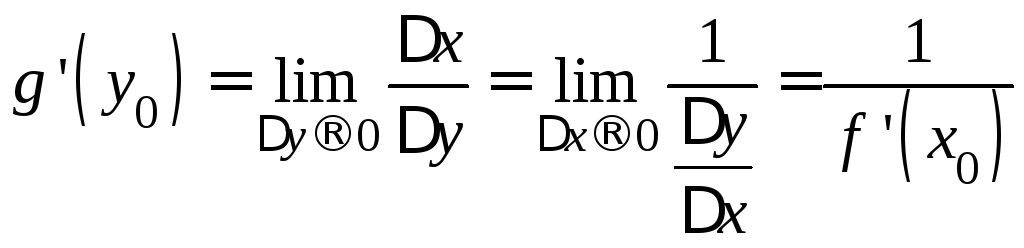

6. (Производная функции, заданной параметрическим способом). Если функции инепрерывны в окрестности точкии− строго монотонная функция, то в окрестности точкиопределена функция. Если, кроме того, функциидифференцируемы в точке, причём, то существуети . Доказательство. В окрестности точки существует непрерывная и строго монотонная обратная функция. Поэтомуможно выразить: . Применяя теоремы 4. и 5 , получим.

Замечание. Так как ,то иногда пишут .