
Математический анализ за 1 и 2 семестр / МатемАнализ3
.docГлава 3. Применения производной.
§1.Вычисление значений функций. Вычисление пределов.
Пример 1. Найти значение числа “![]() ”
с точностью, равной
”
с точностью, равной
![]() .
Как запрограммирован для этой цели
калькулятор?
.
Как запрограммирован для этой цели
калькулятор?
Решение. Можно попытаться использовать доказанную ранее двустороннюю оценку
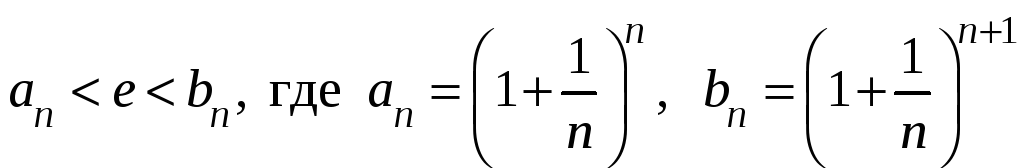 .
.
К сожалению, длина интервала
![]() и для достижения нужной точности
потребовалось бы взять слишком большое
значение
и для достижения нужной точности
потребовалось бы взять слишком большое
значение
![]() .
Формула Маклорена с остаточным членом
в форме Лагранжа дает
.
Формула Маклорена с остаточным членом
в форме Лагранжа дает
 ,
где
,
где
![]() заключено между нулем и
заключено между нулем и
![]() .
Если взять
.
Если взять
![]() ,
то получим
,
то получим
![]() ,
,
![]() .
Так как
.
Так как
![]() ,
а
,
а
![]() ,
то можно взять
,
то можно взять
![]() ,
Поэтому
,
Поэтому
![]()
Пример 2. С помощью правила
Лопиталя-Бернулли вычислить
![]() .
.
Решение. Мы имеем здесь возможность несколько раз применить правило Л-Б. Это дает
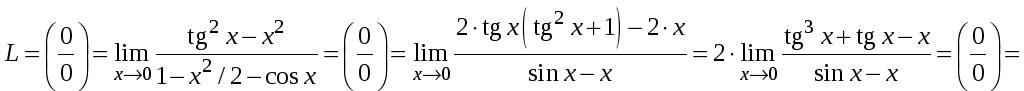

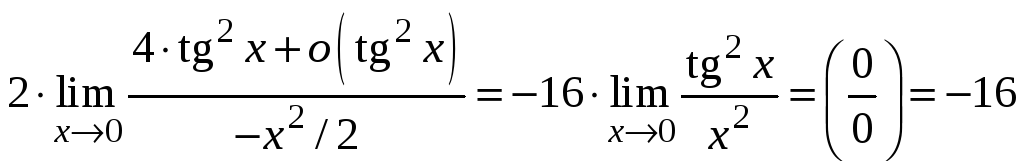 .
.
Пример 3. Вычислить тот же предел
![]() с помощью формулы Маклорена.
с помощью формулы Маклорена.
Решение. Запишем формулу Маклорена
с остаточным членом в форме Пеано для
функций
![]() и
и
![]() :
:
![]()
![]() .
Это дает сразу
.
Это дает сразу
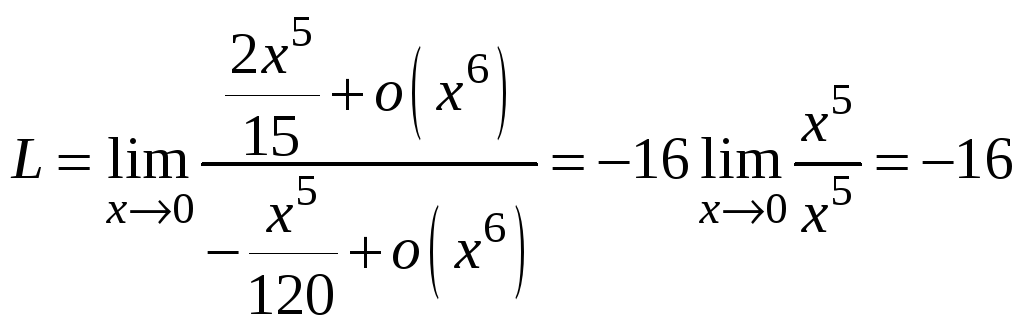 .
.
Заметим, что здесь было достаточно воспользоваться формулой Маклорена-Тейлора пятого порядка.
§2.Возрастание, убывание и экстремумы функции.
Теорема 1. Для того, чтобы функция
![]() была постоянной на интервале
была постоянной на интервале
![]() необходимо и достаточно, чтобы было
необходимо и достаточно, чтобы было
![]() на этом интервале.
на этом интервале.
Доказательство. Необходимость
условия уже известна. Пусть теперь
![]() на интервале
на интервале
![]() и пусть
и пусть
![]() .
По теореме Лагранжа
.
По теореме Лагранжа
![]() ,
где
,
где
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() .
Поэтому
.
Поэтому
![]() на интервале
на интервале
![]() .
.
Теорема 2. (Признак возрастания и
убывания функции). Пусть
![]() .
В таком случае, если
.
В таком случае, если
![]() на интервале
на интервале
![]() ,
то
,
то
![]() строго возрастает на отрезке
строго возрастает на отрезке
![]() .
Точно так же, если
.
Точно так же, если
![]() на интервале
на интервале
![]() ,
то
,
то
![]() строго убывает на отрезке
строго убывает на отрезке
![]() .
.
Доказательство. Пусть известно, что
![]() .
В таком случае по теореме Лагранжа о
конечном приращении,
.
В таком случае по теореме Лагранжа о
конечном приращении,
![]() ,
то для некоторого значения
,
то для некоторого значения
![]() будет
будет
![]() .
Следовательно, если
.
Следовательно, если
![]() ,
то
,
то
![]() ,
т.е.
,
т.е.
![]() строго возрастает на отрезке
строго возрастает на отрезке
![]() .
.
Пример 1. Доказать, что
![]() .
.
Доказательство. Обозначим
![]() .
Тогда будет
.
Тогда будет
![]() ,
,
![]()
![]() .
В таком случае
.
В таком случае
![]() строго возрастает в первой четверти, а
так как
строго возрастает в первой четверти, а
так как
![]() ,
то
,
то
![]()
![]() .
Но тогда и
.
Но тогда и
![]() строго возрастает в первой четверти,
следовательно
строго возрастает в первой четверти,
следовательно
![]() .
Таким образом,
.
Таким образом,
![]()
![]() .
Ч и т. д.
.
Ч и т. д.
Примеры
![]() и
и
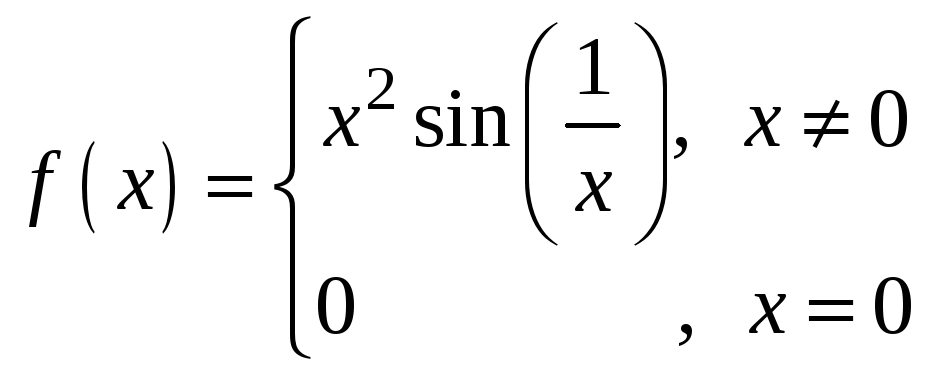 показывают, что необходимое условие
экстремума не является достаточным.
показывают, что необходимое условие
экстремума не является достаточным.
Теорема 3. (Достаточное условие
экстремума). Пусть
![]() в левой полуокрестности точки
в левой полуокрестности точки
![]() ,
,
![]() в её правой полуокрестности и пусть
функция
в её правой полуокрестности и пусть
функция
![]() непрерывна в самой этой точке. Тогда
непрерывна в самой этой точке. Тогда
![]() − точка строгого максимума
− точка строгого максимума
![]() .
Наоборот, если в точке непрерывности
функции
.
Наоборот, если в точке непрерывности
функции
![]() её производная
её производная
![]() меняет знак
меняет знак![]() ,
то
,
то
![]() − точка строгого минимума функции
− точка строгого минимума функции
![]() .
.
Доказательство. В первом случае
![]() строго возрастает слева от точки
строго возрастает слева от точки
![]() ,
поэтому
,
поэтому
![]() в левой полуокрестности. А так как
в левой полуокрестности. А так как
![]() строго убывает слева от точки
строго убывает слева от точки
![]() ,
то
,
то
![]() .
Поэтому
.
Поэтому
![]() − точка строго максимума функции
− точка строго максимума функции
![]() .
Второй случай разбирается точно так
же.
.
Второй случай разбирается точно так
же.
Теорема 4. (Достаточное условие
экстремума, использующее старшие
производные). Пусть
![]() .
Если
.
Если
![]() − четное, то
− четное, то
![]() − точка максимума функции
− точка максимума функции
![]() .
Если же
.
Если же
![]() − нечетное, то в точке
− нечетное, то в точке
![]() нет экстремума.
нет экстремума.
Доказательство.
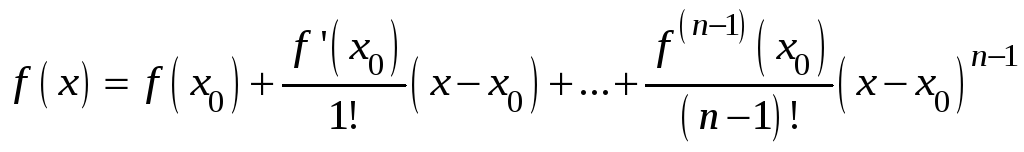
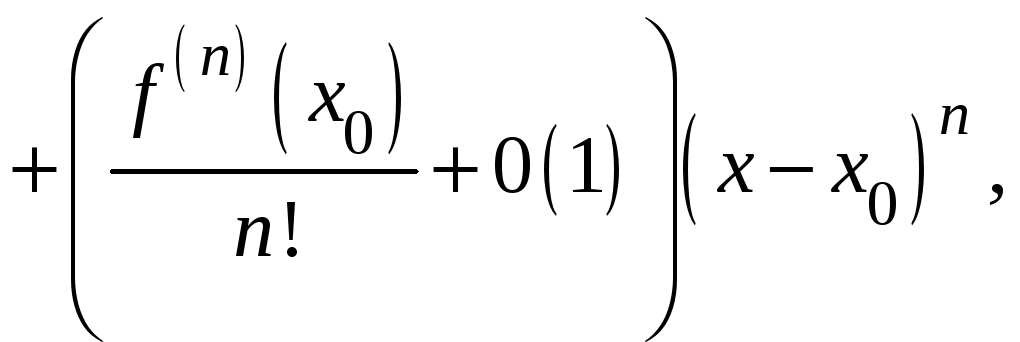
![]() .
.
По условию теоремы
 когда
когда
![]() .
При значениях
.
При значениях
![]() ,
близких к числу
,
близких к числу
![]() ,
знак величины
,
знак величины
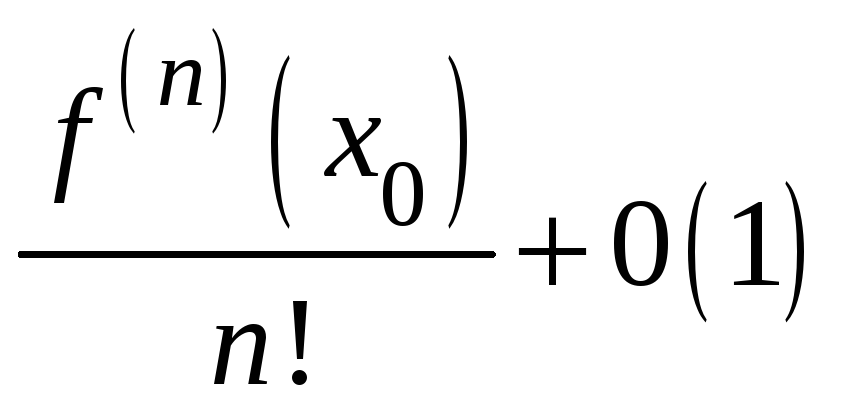 совпадает со знаком производной
совпадает со знаком производной
![]() .
Поэтому если
.
Поэтому если
![]() четное число, то разность
четное число, то разность
![]() сохраняет свой знак в окрестности точки
сохраняет свой знак в окрестности точки
![]() и, следовательно,
и, следовательно,
![]() имеет в этой точке экстремум. Именно,
если
имеет в этой точке экстремум. Именно,
если
![]() ,
то
,
то
![]() − точка максимума
− точка максимума
![]() ,
если же
,
если же
![]() ,
то
,
то
![]() − точка минимума
− точка минимума
![]() .
Пусть теперь
.
Пусть теперь
![]() − число нечетное. В этом случае разность
− число нечетное. В этом случае разность
![]() меняет знак при прохождении
меняет знак при прохождении
![]() через точку
через точку
![]() ,
поэтому
,
поэтому
![]() не является точкой экстремума.
не является точкой экстремума.
Частный случай. Пусть
![]() − стационарная точка функции
− стационарная точка функции
![]() (то есть
(то есть
![]() ).
Тогда, если
).
Тогда, если
![]() ,
,
![]() − точка максимума
− точка максимума
![]() ,
если же
,
если же
![]() ,
,
![]() − точка минимума
− точка минимума
![]() .
Для запоминания можно использовать так
называемое “правило воды”.
.
Для запоминания можно использовать так
называемое “правило воды”.

Пример 2. Исследовать на экстремум
функцию
![]() в точке
в точке
![]() .
.
Решение. Имеем:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
Поэтому
.
Поэтому
![]() − точка минимума рассматриваемой
функции.
− точка минимума рассматриваемой
функции.
|
Bbb
|
§3 Задачи на наибольшее и наименьшее значения функции.
Для нахождения наибольшего и наименьшего значений функции на отрезке необходимо найти все её критические точки (т.е. точки, где производная этой функции рана нулю или не существует), присоединить к ним концы промежутка, вычислить значения функции во всех отобранных точках и отобрать среди этих значений самое большое и самое маленькое.
Пример. Найти наибольший объём
конуса с заданной боковой поверхностью
![]() .
Чему равен центральный угол его развёртки?
.
Чему равен центральный угол его развёртки?
Решение. Обозначим
![]() образующую конуса,
образующую конуса,
![]() его высоту,
его высоту,
![]() радиус основания и
радиус основания и
![]() объём, Тогда будет
объём, Тогда будет
![]() ,
,
![]() и
и
![]() .
Поэтому можно выразить объём
.
Поэтому можно выразить объём
![]() через радиус
через радиус
![]() непосредственно:
непосредственно:
 =
=![]() ,
где
,
где
![]() ,
,
![]() .
.
Для того, чтобы решить поставленную
задачу, достаточно найти наибольшее
значение функции
![]() при условии, что
при условии, что
![]() .
Так как
.
Так как
![]() ,
то стационарное значение функции
,
то стационарное значение функции
![]() равно
равно
![]() .
Мы видим, что
.
Мы видим, что
![]() .
Поэтому
.
Поэтому
![]() ,
а
,
а
![]() .
Осталось вычислить центральный угол
.
Осталось вычислить центральный угол
![]() сектора, представляющего собой развёртку
найденного конуса. Так как
сектора, представляющего собой развёртку
найденного конуса. Так как
![]() ,
то
,
то
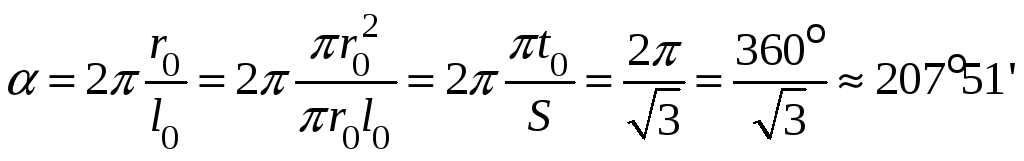 .
.

§4. Направление выпуклости и точки перегиба функции.
Определение 1. Функция
![]() называется выпуклой вниз на отрезке
называется выпуклой вниз на отрезке
![]() ,
если на этом отрезке любая дуга ее
графика лежит ниже хорды (мы будем
это записывать с помощью значка
,
если на этом отрезке любая дуга ее
графика лежит ниже хорды (мы будем
это записывать с помощью значка
![]() ),
Аналогично определяется выпуклость
вверх (
),
Аналогично определяется выпуклость
вверх (![]() ).
).
Для получения аналитического условия выпуклости нам понадобятся 2 леммы.
Лемма 1. Если существует
![]() ,
то
,
то
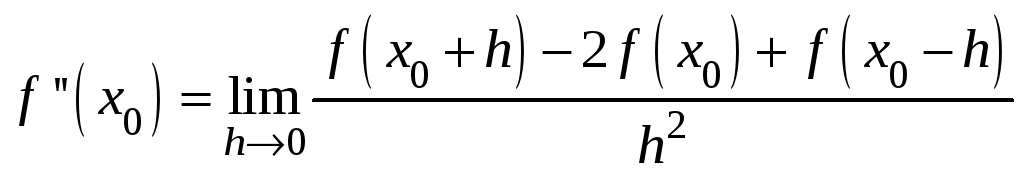 .
.
Доказательство. По формуле Тейлора
![]()
![]() .
Складывая, получаем
.
Складывая, получаем
![]() и т. д.
и т. д.
Лемма 2. Если
![]() и
и
![]() − уравнение хорды графика этой функции
на участке
− уравнение хорды графика этой функции
на участке
![]() ,
то найдется число
,
то найдется число
![]() такое, что
такое, что
![]() .
.
Доказательство. Введем в рассмотрение
функцию
![]() .
Легко при фиксированном значении
.
Легко при фиксированном значении
![]() подобрать параметр
подобрать параметр
![]() так, чтобы было
так, чтобы было
![]() ;
именно
;
именно
![]() .
Так как функция
.
Так как функция
![]() обращается в нуль в точках
обращается в нуль в точках
![]() ,
то применяя дважды теорему Ролля, видим,
что в при некотором
,
то применяя дважды теорему Ролля, видим,
что в при некотором
![]() будет
будет![]() .
Но
.
Но
![]() .
Поэтому
.
Поэтому
![]() или
или
![]() .
Подставляя
.
Подставляя
![]() вместо
вместо
![]() в выражение для
в выражение для
![]() ,
получаем
,
получаем
![]() .
.
Теорема 1. Если
![]() то
то
![]() на отрезке
на отрезке
![]() тогда и только тогда, когда
тогда и только тогда, когда
![]() на отрезке
на отрезке
![]() .
.
Доказательство. Если
![]() ,
то
,
то
![]() ,
,
![]() .
Из леммы 1 следует, что
.
Из леммы 1 следует, что
![]() .
.
Наоборот, пусть
![]() на интервале
на интервале
![]() .
Применим лемму 2 к отрезку
.
Применим лемму 2 к отрезку
![]() ,
где
,
где
![]() .
Тогда мы имеем
.
Тогда мы имеем
![]() ,
т. е.
,
т. е.
![]()
![]()
![]() .
.
Для запоминания можно использовать “правило воды”.
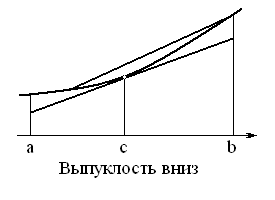
Добавление. Можно в определении
выпуклости заменить хорду графика
касательной. Легко доказать, что
функция
![]() выпукла вниз на отрезке
выпукла вниз на отрезке
![]() тогда и только тогда, когда на этом
участке любая дуга графика лежит выше
касательной, проведенной к графику
в промежуточной точке.
тогда и только тогда, когда на этом
участке любая дуга графика лежит выше
касательной, проведенной к графику
в промежуточной точке.
Определение 2. Пусть производная
![]() непрерывна
непрерывна
![]() .
Точка
.
Точка
![]() называется точкой перегиба функции
называется точкой перегиба функции
![]() ,
если в левой и правой полуокрестностях
,
если в левой и правой полуокрестностях
![]()
![]() имеет противоположное направление
выпуклости.
имеет противоположное направление
выпуклости.
Теорема 2. (Необходимое условие перегиба в точке). В точке перегиба функции её вторая производная равна нулю или не существует.
Доказательство. По теореме 1 в точке
перегиба функции
![]() ее производная
ее производная
![]() имеет экстремум. Поэтому там
имеет экстремум. Поэтому там
![]() рана нулю или не существует.
рана нулю или не существует.
Это условие не является достаточным.
Контрпримером может служить, функция
![]() .
.
Теорема 3. (Достаточное условие
перегиба, использующее только
![]() ).
Пусть производная
).
Пусть производная
![]() непрерывна в точке
непрерывна в точке
![]() и
и
![]() сохраняет знак в полуокрестностях этой
точки. Если эти знаки противоположны
то
сохраняет знак в полуокрестностях этой
точки. Если эти знаки противоположны
то
![]() − точка перегиба, если одинаковые, то
− перегиба нет.
− точка перегиба, если одинаковые, то
− перегиба нет.
(Следует из определения точки перегиба и теоремы 1.)
Теорема 4. (Достаточное условие
перегиба, использующее старшие
производные). Пусть
![]() ,
,
![]() .
В таком случае, если
.
В таком случае, если
![]() − четное число, то
− четное число, то
![]() не является точкой перегиба функции
не является точкой перегиба функции
![]() ,
если же
,
если же
![]() нечетное, то
нечетное, то
![]() − точка перегиба.
− точка перегиба.
Доказательство. Из условия следует,
что
 .
.
Если здесь
![]() четное, то знак
четное, то знак
![]() сохраняется в окрестности точки
сохраняется в окрестности точки
![]() и перегиба здесь нет. Если
и перегиба здесь нет. Если
![]() нечетное, то знак
нечетное, то знак
![]() разный справа и слева от точки
разный справа и слева от точки
![]() и
и
![]() − точка перегиба функции
− точка перегиба функции
![]() .
.
§5.Асимптоты графика функции.
Определение. Прямая
![]() называется асимптотой графика
функции
называется асимптотой графика
функции
![]() ,
если при неограниченном удалении точки
,
если при неограниченном удалении точки
![]() от начала координат вдоль прямой
от начала координат вдоль прямой
![]() расстояние этой точки от графика функции
стремится к нулю.
расстояние этой точки от графика функции
стремится к нулю.
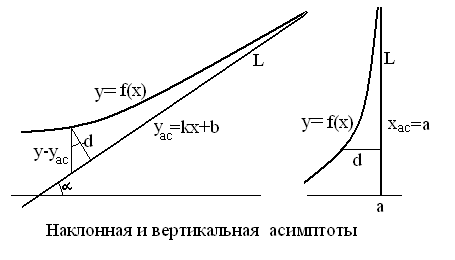
График функции
![]() имеет наклонную асимптоту
имеет наклонную асимптоту
![]() тогда и только тогда, когда существуют
конечные пределы
тогда и только тогда, когда существуют
конечные пределы
![]() и
и
![]() .Действительно,
пусть
.Действительно,
пусть
![]() − расстояние точки графика
− расстояние точки графика
![]() от прямой
от прямой
![]() ,
тогда
,
тогда
![]() .
Поэтому
.
Поэтому
![]()
![]()
 .
.
График
![]() имеет горизонтальную асимптоту с
уравнением
имеет горизонтальную асимптоту с
уравнением
![]() ,
если
,
если
![]() .
График имеет вертикальную асимптоту
.
График имеет вертикальную асимптоту
![]() ,
если
,
если
![]() − точка бесконечного разрыва функции
− точка бесконечного разрыва функции
![]() .
.
§6. Схема полного исследования функции. Построение графика.
-
Область определения функции.
-
Симметрия графика, периодичность.
-
Точки разрыва функции.
-
Точки пересечения с осями координат, интервалы знакопостоянства.
-
Асимптоты и подходы к ним.
-
Интервалы монотонности и точки экстремума функции.
-
Интервалы выпуклости и точки перегиба функции.
-
Нахождение дополнительных точек графика.
-
Построение графика функции.
Пример. Провести исследование
функции
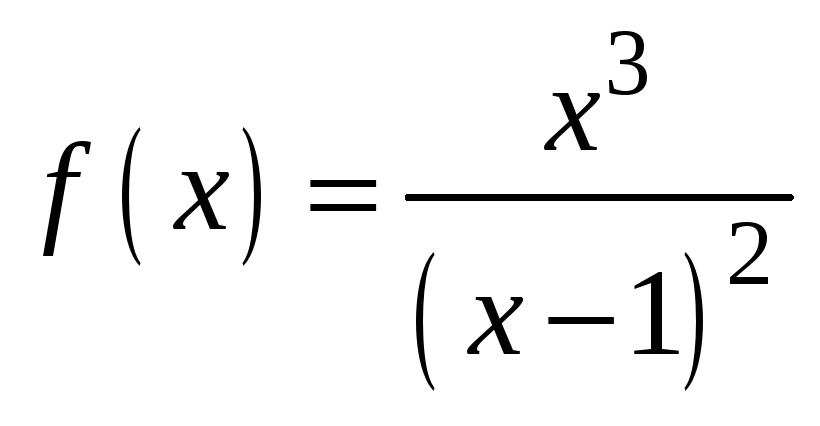 и построить ее график
и построить ее график
-
Область определения функции
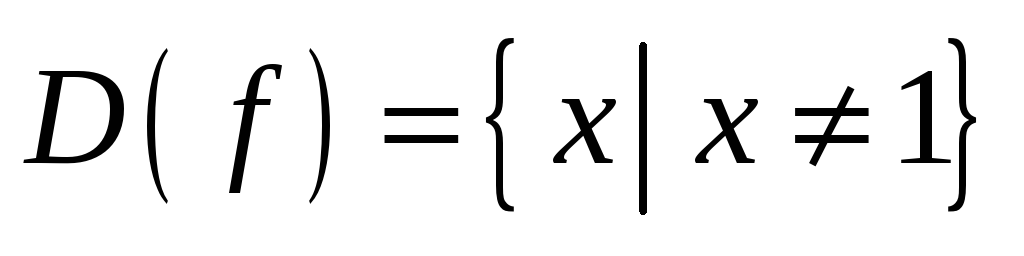
-
Функция непериодическая, ни чётная, ни нечетная (функция общего вида).
-
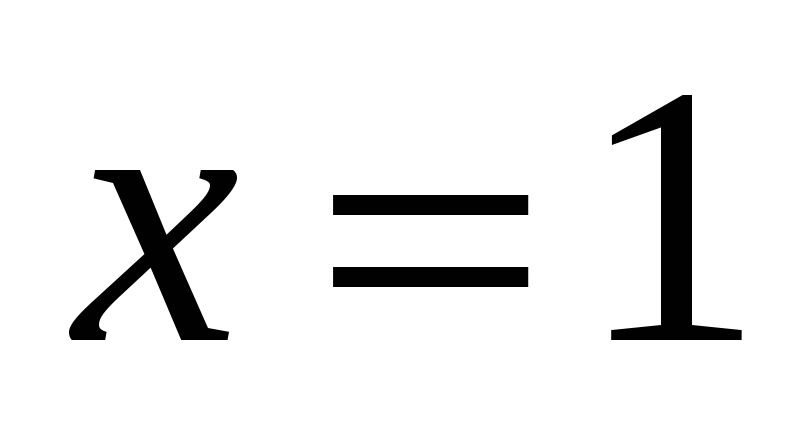 − точка бесконечного разрыва
функции.
− точка бесконечного разрыва
функции. -
 − единственная точка пересечения с
осями координат.
− единственная точка пересечения с
осями координат.
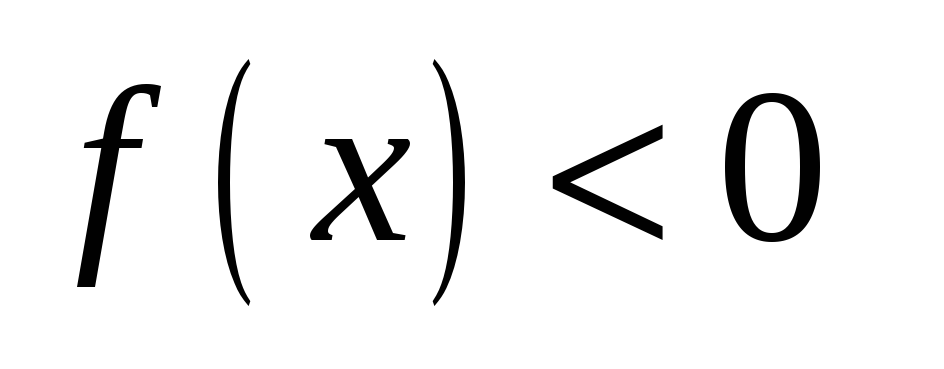
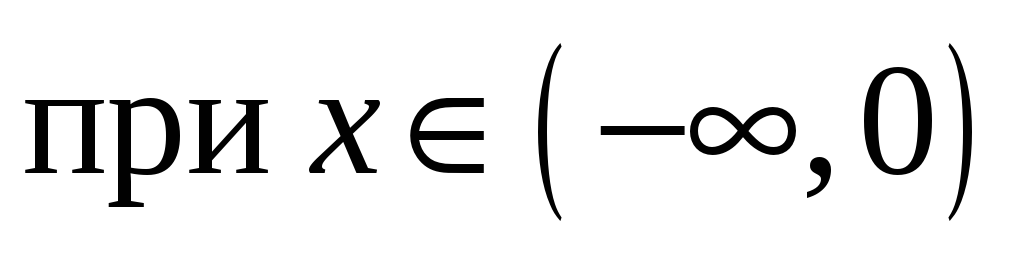 ,
,
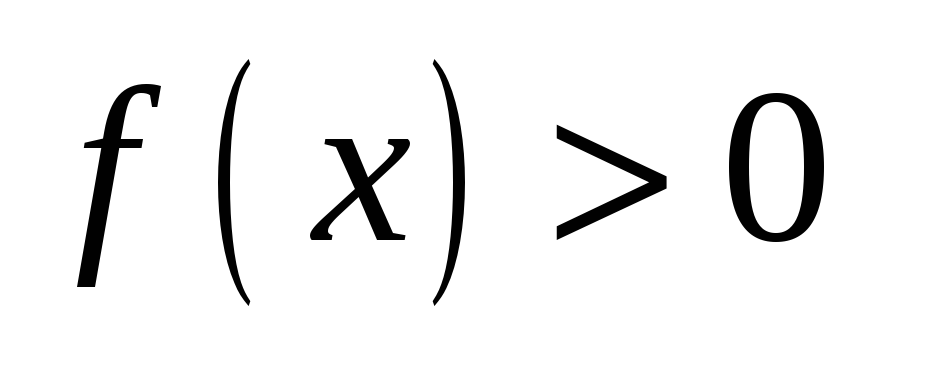
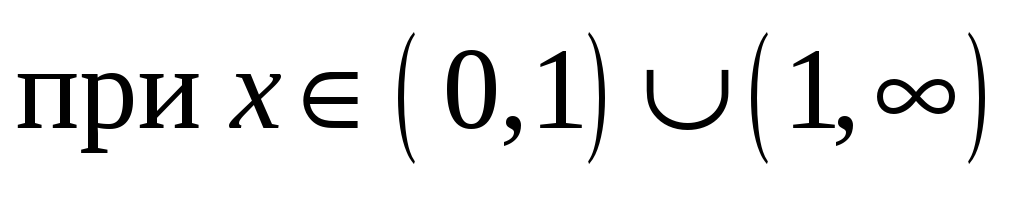 .
. -
Вертикальная асимптота:
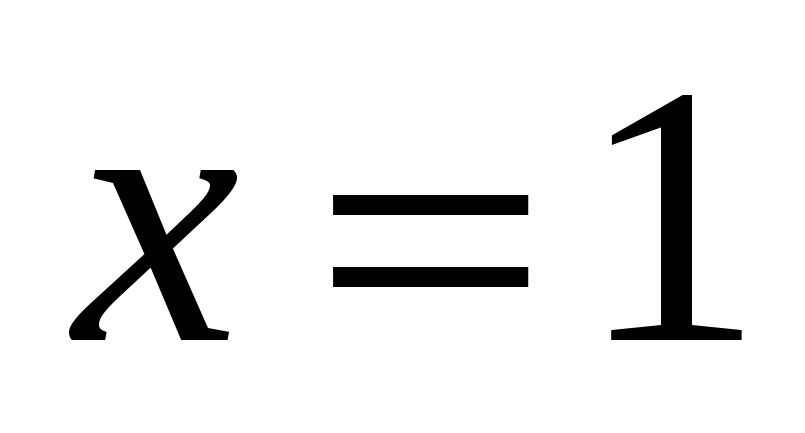 .
Подходы к асимптоте:
.
Подходы к асимптоте:
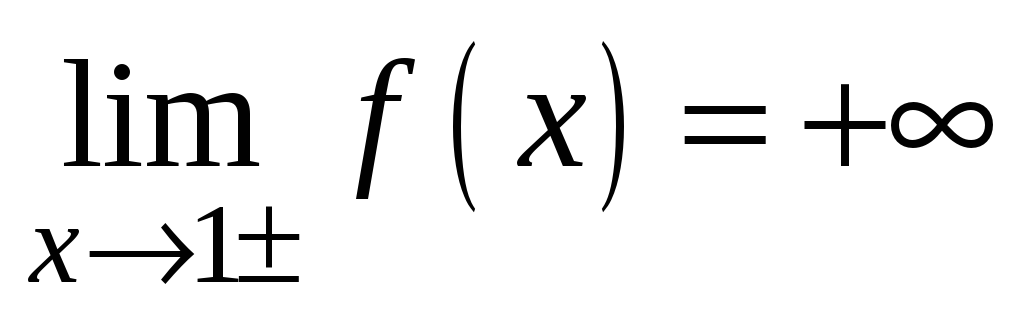 .
Наклонная асимптота:
.
Наклонная асимптота:
 .
.
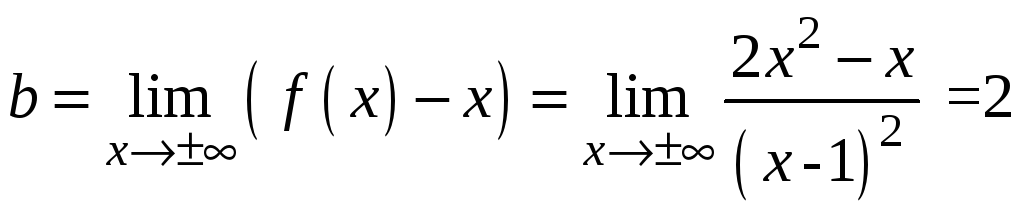 ,
,
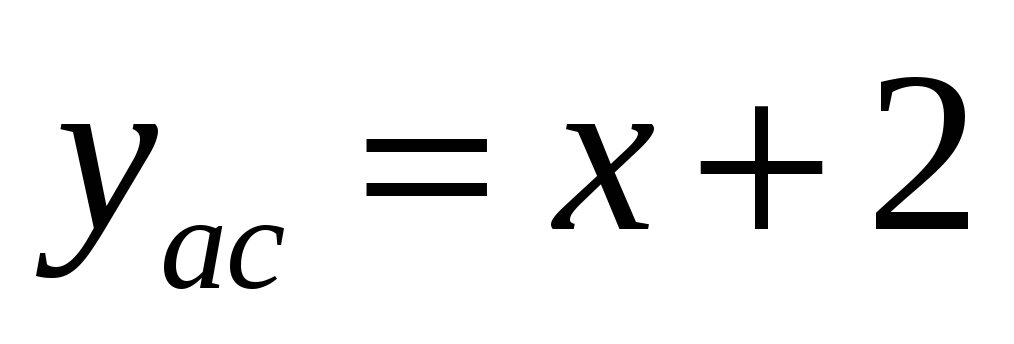 .
Подходы к асимптоте:
.
Подходы к асимптоте:
 .
Пересечения с асимптотой −
.
Пересечения с асимптотой −
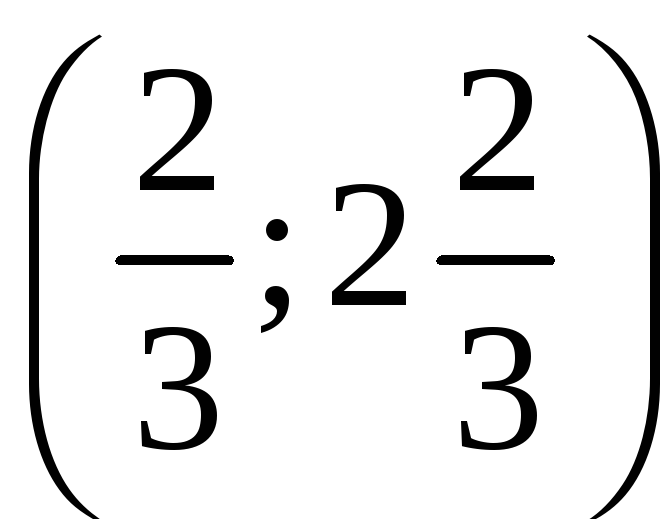 .
.

