Литература

1. Бугров, Никольский. Дифференциальное и интегральное исчисление, ч.1.

2. Кудрявцев, Курс математического анализа, ч.1.

3. Сборник задач по математике для ВТУЗОВ под ред. Ефимова и Поспелова, ч.2.

Глава 1. Теория пределов §1. Принцип твг.

В школьном курсе математики вы встречались с числовыми системами: . Вам известны свойства арифметических операций и свойства неравенств. Для дальнейшего нам понадобится одно дополнительное свойство множества действительных чисел..

Если любое число из множестване превосходит числа, (в сокращенной записи), тоназываетсяверхней гранью множества , а само множество называетсяограниченным сверху (числом ). Множествоназываетсяограниченным снизу числом , если. Числов этом случае называетсянижней гранью множества . Мы будем называть множествоограниченным, если ограниченно и сверху и снизу. Введем еще одно определение. Мы скажем, что множествоотделено от нуля, если существует такое положительное число , что для всехвыполнено неравенство.

Упражнение. Множество ограниченно тогда и только тогда, когда такое, что.

Если множество ограничено сверху числом, то у него есть и другие верхние грани, например. Но находить верхнюю грань “с запасом” не интересно. Интереснее находить наименьшую верхнюю грань.

Определение. Точной верхней гранью (ТВГ) множества называется наименьшая из всех верхних граней этого множества. Она обозначается.

В ограниченное множество может не иметь ТВГ. Пусть множествосостоит из десятичных приближений по недостатку для иррационального числа. Множествоограниченно, но точной верхней грани в числовой системеу него нет (так как). Ву него есть ТВГ;.

Принцип ТВГ.Ввсякое ограниченное сверху множество имеет точную верхнюю грань. (Точно так же всякое ограниченное снизу множество имеет точную нижнюю грань.)

Это свойства множества можно считать аксиомой. Принципом ТВГ мы часто будем пользоваться в дальнейшем.

§2. Предел числовой последовательности.

Определение. Числоназываетсяпределомпоследовательности чисел(в записиили), если при любомпри почти всехвыполняется неравенство, т.е..

Определение. Последовательностьназываетсябесконечно малой (б.м.), если.

Определение. Мы будем называтьбесконечно большой(б.б.) последовательностью, и писать, если.

Последовательности, имеющие конечный предел, называются сходящимися.

Упражнение 1. Последователь не может иметь более одного предела.

Упражнение 2. Если последовательность имеет предел (конечный или бесконечный), то любая ее подпоследовательность имеет тот же предел.

Упражнение 3. Пустьи пусть. В таком случае─ бесконечно малая последовательность тогда и только когда, когда последовательность− бесконечно большая. Таким образом, б.м. и б.б. последовательности взаимно обратны по величине.

Лемма 1. тогда и только тогда, когда, где− б.м. последовательность.

Доказательство. ,где.

Лемма 2. Всякая сходящаяся последовательность ограниченна.

Доказательство. Пустьи пусть. Т.к., то, если. Поэтому.

§3. Предельный переход и неравенства.

Теорема 1. Если, тодля почти всех.

Доказательство. Обозначим,. Из условий следует, что для почти всех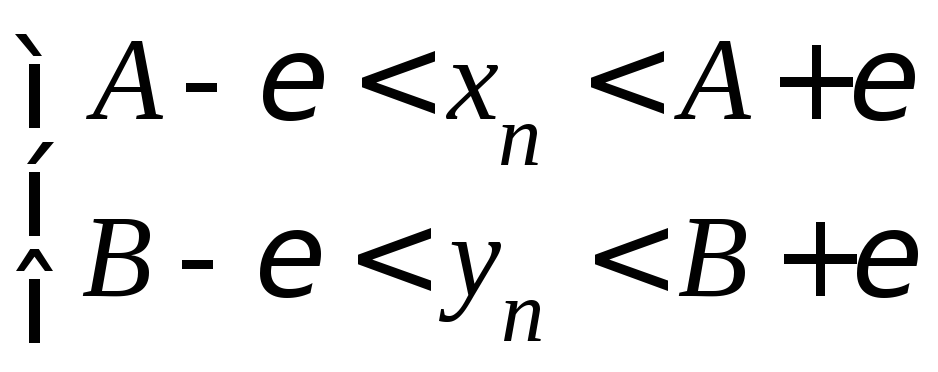. Поэтомудля почти всех.

Теорема 2. Еслидля почти всех, то.

Доказательство. Предположим противное, т.е. предположим, что. Тогда по теореме 1 будетдля почти всех, а это неравенство противоречит условию теоремы.

Следствие. Если ,то последовательностьдля почти всехотделена от нуля и сохраняет знак.

Доказательство. Пусть, например. Тогда. В таком случае по теореме 1

для почти всех.

Теорема 3. (Теорема о двусторонней оценке или “теорема о двух полицейских”).

Пусть для п.в. и пусть. Тогда.

Доказательство. Из условия теоремы следует, чтодля почти всехвыполнена система неравенств. Поэтому для почти всех.