Глава 7. Кратные интегралы. §1. Определение и основные свойства двойного интеграла, Тройной интеграл.

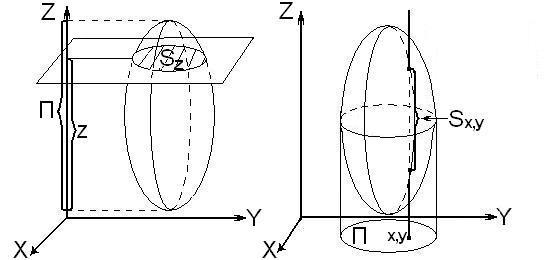
1˚. Двойной интеграл. Пусть− квадрируемое, ограниченное множество и− функция, определенная на этом множестве. Рассмотрим разбиениена неперекрывающиеся квадрируемые подмножества. Обозначим− площадь множестваи− диаметр этого множества. Назовеммелкостью разбиениявеличину. Образуеминтегральную суммуРимана .

Определение. Если существует предел, то функцияназываетсяинтегрируемойпо Риману на множестве, в записи −, а сам предел называетсядвойным интеграломи обозначаетсяили.

Легко доказать, что интегрируемая функция ограничена на множестве . Поэтому имеют смыслсуммы Дарбу ,а также суммагде,,и− колебание функциина множестве. По той же схеме, что и для определенного интеграла, доказываются следующие теоремы:

Критерий интегрируемости. Функцияинтегрируема на множестветогда и только тогда, когда суммастремится к нулю.

Теорема (об интегрируемости непрерывной функции). Пусть, где− ограниченное множество с замкнутой, кусочно-гладкой границей. В таком случае.

Так же, как и раньше, из определения интеграла и критерия интегрируемости выводятся такие свойства двойного интеграла, как линейность, аддитивность, неотрицательность (монотонность). Сформулируем еще теорему о среднем.

Теорема о среднем интегральном. Пусть, где−связноемножество с кусочно-гладкой границейи конечной с площадью. В таком случае существует точка, такая что. (Напомним, что− связное множество, если любые 2 его точки можно соединить ломаной линией.)

2˚1. Мера Жордана в пространстве .

Рассмотрим разбиение пространства на кубы рангас помощью плоскостей,,,. Обозначимколичество кубов содержащихся во множествеи− количество кубов, пересекающихся с множеством. Пусть ещё.

Определение. ВнутреннеймеройЖорданамножестваназывается величина.Внешней мерой Жордана множестваназывается величина. Множествоназываетсяизмеримым по Жордануиликубируемым, если. Их общее значениеназывается простомерой этого множества или его объёмом.

2˚1. Тройной интеграл. Пусть− кубируемое, ограниченное множество и− функция, определенная на этом множестве. Рассмотрим разбиениена неперекрывающиеся кубируемые подмножества. Обозначим− объём множестваидиаметр этого множества. Назовеммелкостью разбиениявеличину. Образуеминтегральную суммуРимана .

Определение. Если существует предел, то функцияназываетсяинтегрируемойпо Риману на множестве, в записи −, а сам предел называетсятройным интеграломи обозначаетсяили.

И в этом случае точно так же, как в двумерном случае, формулируются и доказываются критерий интегрируемости, теорема о существования тройного интеграла от непрерывной функции и основные свойства интеграла. Отметим только, что средним интегральным в трёхмерном случае называют величину

.

Замечание. По той же схеме определяется мера Жордана и интеграл в пространствепри любом натуральном.

§2. Сведение кратных интегралов к повторным интегралам.

1˚. Напомним, что множествоназываетсяпростымв данном направлении, если пересечениес любой прямой этого направления представляет собой отрезок, точку или пустое множество. Если множествопростое по направлению, то его границасостоит из кривых,и, возможно, отрезков прямых, т.е..

Теорема 1. Пусть, и пусть существует двойной интеграл. Предположим ещё, что при любом фиксированном значениисуществует определённый интеграл. В таком случае существует иповторныйинтеграл. При этом

.

Доказательство.

1-я часть. Пусть сначала− прямоугольник. Рассмотрим разбиенияи. Обозначим,и. Тогдабудет

и. Суммируяи, получаем. Крайние члены полученного неравенства − суммы Дарбу для интеграла. Как мы знаем, они стремятся к этому двойному интегралу, где− мелкость разбиения. Следовательно, существует повторный интеграл, то есть интеграли он совпадает с двойным интегралом. Ч.и т.д.

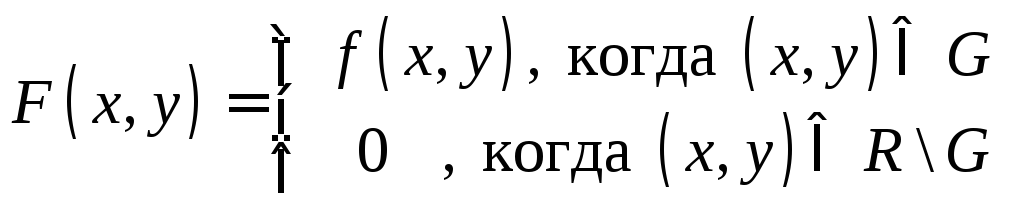2-я часть. Ограниченное множествоможно дополнить до прямоугольника. Доопределим функциюследующим образом:. Ясно, что функцияинтегрируема в прямоугольникеи что(свойство аддитивности интеграла). Кроме того,. Следовательно, согласно 1-й части,.

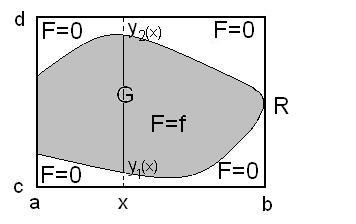
Следствие. (Теорема Фубини об изменении порядка интегрирования.)

Пусть − множество, простое по обоим координатным направлениям, т.е..

Если существует двойной интеграл и, кроме того, существуют все интегралы по сечениями все интегралы по сечениям, то существуют и равны между собой оба повторных интеграла:

.

2˚. Обобщение. Пусть,;− сечение множестваподпространством,− проекцияна подпространство(т.е. на подпространство первых координат).

Теорема 2. Пусть существует интеграли пусть при любом значениисуществует интеграл по сечению. В таком случае существует повторный интеграл. При этом.

Отметим частные случаи: 1) и 2).