4˚. Признаки, основанные на сравнении с геометрической прогрессией.

Теорема (Признак Даламбера). Рассмотрим ряд с положительными членамии предположим, что существует предел. В таком случаеряд сходится, а− расходится. Существуют как сходящиеся, так и расходящиеся ряды(случай неопределённости).

Доказательство. Пусть сначала. Выберем число. Существует номер, такой чтобудет. Тогдаполучим

.Так как, то последовательностьограничена, т.е. существует такое число, что. Таким образом, рядмажорируется убывающей геометрической прогрессией и потому сходится. Заметим, что из неравенствтакже следует оценка остатка:,.

Пусть теперь . Выберем число. Существует номер, после которого будети, значит,. Таким образом, члены ряда вместо того, чтобы стремится к нулю с увеличением номера, быстро увеличиваются

(со скоростью возрастающей геометрической прогрессии).

Обратимся теперь к рядам Дирихле . В этом случаепри любом значении. Но, как мы уже знаем, некоторые из этих рядов сходятся, другие − расходятся..

Теорема. (Признак Коши − радикальный). Рассмотрим ряд с неотрицательными членамии предположим, что существует предел. В таком случаеряд сходится,ряд сходится. Существуют как сходящиеся, так и расходящиеся ряды, для которых(случай неопределённости).

Доказательство. Пусть сначалаи. Существует такой номер, чтобудетили. Так как, то данный ряд сходится. Кроме того, ясно, что в этом случае.

Если и, то, как и в теореме Даламбера, начиная с некоторого номера члены ряда больше членов возрастающей геометрической прогрессии.

Контрпример снова предоставляют ряды Дирихле, для которых при всех значении.

Замечание 1. В формулировке этой теоремы можно заменить.

Замечание 2. Можно доказать следующую теорему:если существует, то существует и, причем эти пределы совпадают. Таким образом, признак Коши является более общим утверждением, чем признак Даламбера.

§3.Знакопеременные ряды. Абсолютная и условная сходимость.

1˚. Теорема (Признак Лейбница). Пустьзнакопеременныйряд, то есть, и пустьубывает и стремится к нулю.. В таком случае данный ряд сходится, при этоми.

Доказательство. Пусть сначала. Тогда, следовательно,. Если,. В любом случае,заключено между нулём и. Потому сумма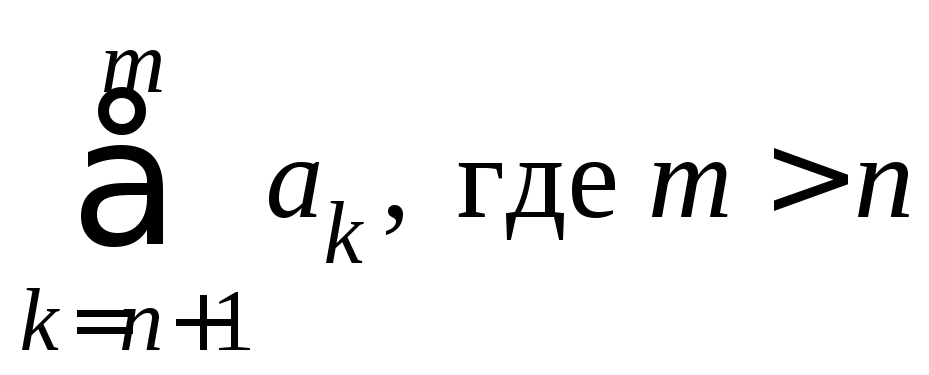заключена между числами. Сходимость ряда следует из критерия Коши. Переходя к пределу, видим, что остатокзаключен между числами. Ч и т.д.

Замечание. Из доказанной теоремы следует, в частности, сходимость “ряда Лейбница”, с которым мы встречались в §1.

2˚. Теорема. Если рядсходится, то сходится и ряд. Обратное утверждение не верно.

Доказательство. Сходимость ряда сразу следует из критерия Коши для рядов ввиду неравенства. Контрпримером здесь может служить ряд Лейбница, который, как мы знаем, сходится, в то время как ряд из модулей его членов, т.е. гармонический ряд, расходится.

Определение. Рядназываетсяабсолютно сходящимся, если сходится ряд из модулей его членов. Ряд называетсяусловно сходящимся, если он сходится, но не абсолютно.

3˚. Приведём без доказательства два свойства абсолютно сходящихся рядов.

• В абсолютно сходящемся ряде можно производить любыеперестановки его членов (т.е. перестановки не меняют сумму ряда).

• Два абсолютно сходящихся ряда можно почленно перемножить (как многочлен на многочлен). При этом суммы рядов также перемножатся.