3˚. Пример.
а). Разложить функцию на промежутке
на промежутке 1)
1)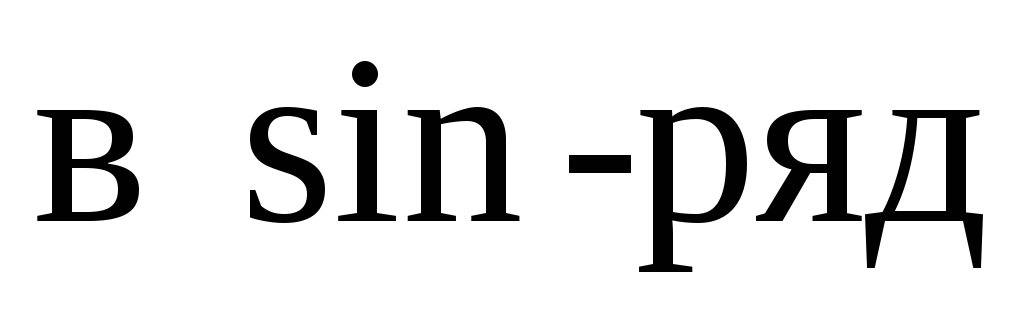 Фурье, 2)
Фурье, 2) Фурье.
Фурье.
б). Сравнить в каждом из этих случаев
графики суммы ряда
 с графиками частичных сумм.
с графиками частичных сумм.
в). Получить тождества для числовых
рядов, подставляя различные значения
 в обе части найденных разложений.
в обе части найденных разложений.
г). Получить тождества для числовых
рядов с помощью равенства Парсеваля -
Стеклова.
Решение.
1). а). Продолжим функцию сначала нечетно, затем периодически.
Полученная нечётная периодическая
кусочно-гладкая на периоде функция
сначала нечетно, затем периодически.
Полученная нечётная периодическая
кусочно-гладкая на периоде функция совпадает
совпадает на промежутке
на промежутке и имеет скачки в точках
и имеет скачки в точках .
Ряд Фурье этой функции всюду сходится
и его сумма
.
Ряд Фурье этой функции всюду сходится
и его сумма совпадает
совпадает на интервале
на интервале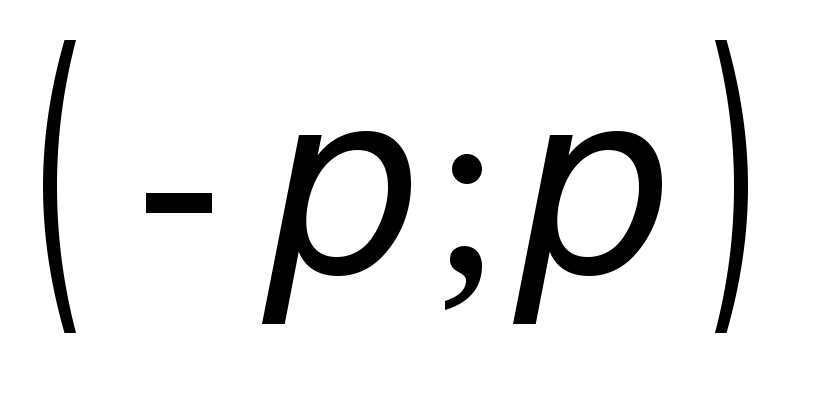 .
Так как
.
Так как и
и ,
то
,
то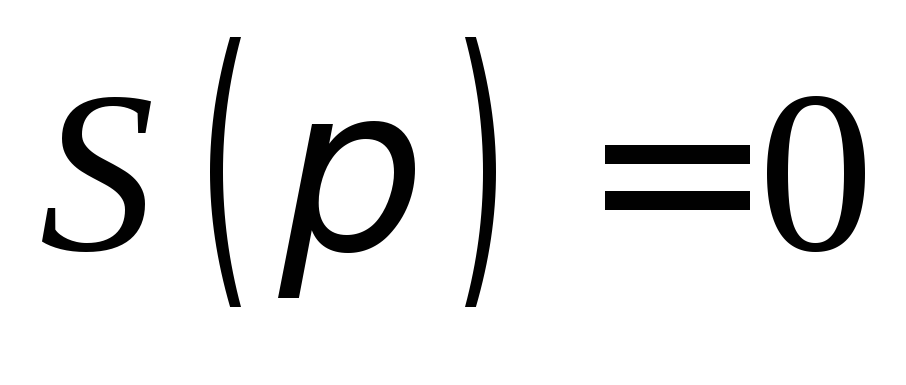 ;
вообще,
;
вообще, .
В этом случае все
.
В этом случае все коэффициенты
Фурье
коэффициенты
Фурье равны нулю, а числа
равны нулю, а числа будут равны
будут равны .
Интегрирования по частям даёт
.
Интегрирования по частям даёт .
Окончательно получаем
.
Окончательно получаем .
.
б). Сравнение
графиков функций ,
,
 и
и .
.

в). При
значении будет
будет ,
и мы снова получаем
,
и мы снова получаем (см.§6).
(см.§6).
г). Равенство Парсеваля − Стеклова
даёт в этом примере .
Поэтому
.
Поэтому (Эйлер). Отметим, что
(Эйлер). Отметим, что
 .
.
2) а). Продолжим
функцию сначала чётно, затем периодически.
Полученная чётная периодическая
кусочно-гладкая на периоде функция
сначала чётно, затем периодически.
Полученная чётная периодическая
кусочно-гладкая на периоде функция совпадает
совпадает на отрезке
на отрезке и не имеет точек разрыва. По этой причине
ряд Фурье
и не имеет точек разрыва. По этой причине
ряд Фурье сходится всюду, а его сумма
сходится всюду, а его сумма на отрезке
на отрезке равна
равна .
Все
.
Все коэффициенты
коэффициенты равны нулю,
равны нулю,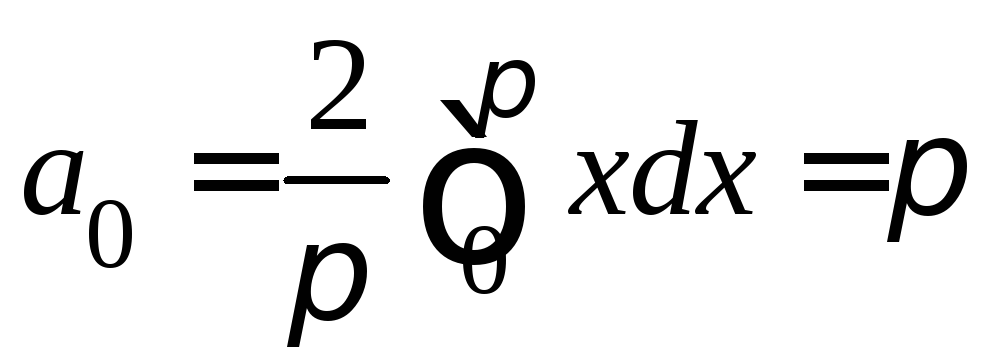 ,
, ,
т.е.
,
т.е. .
Поэтому
.
Поэтому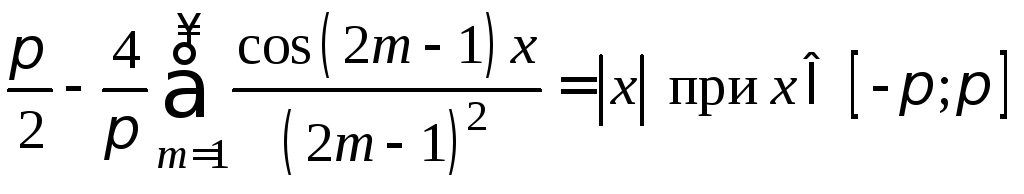 .
.
б). Сравнение графиков функций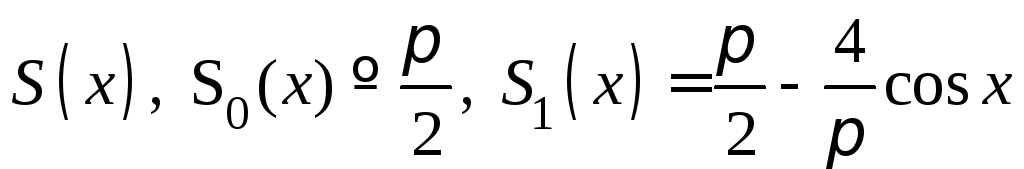 и
и .
.
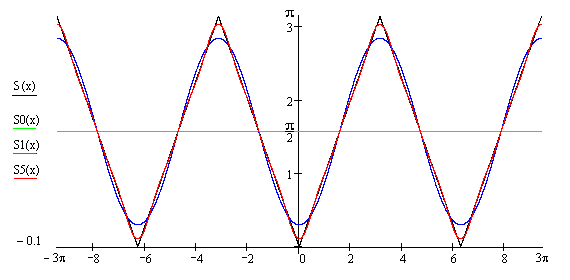
в).Пусть ,
тогда будет
,
тогда будет или
или .
Откуда снова следует тождество Эйлера.
Действительно, если обозначить
.
Откуда снова следует тождество Эйлера.
Действительно, если обозначить ,
то увидим, что
,
то увидим, что или
или .
Следовательно,
.
Следовательно, .
.
г). Равенство Парсеваля − Стеклова
в данном случае записывается в виде
 или
или .
Если обозначить
.
Если обозначить ,
то получим
,
то получим .
Поэтому
.
Поэтому (Эйлер).
(Эйлер).
128


 .
. и
и .
.
 (см.§6).
(см.§6). .
Поэтому
.
Поэтому (Эйлер). Отметим, что
(Эйлер). Отметим, что
 .
Поэтому
.
Поэтому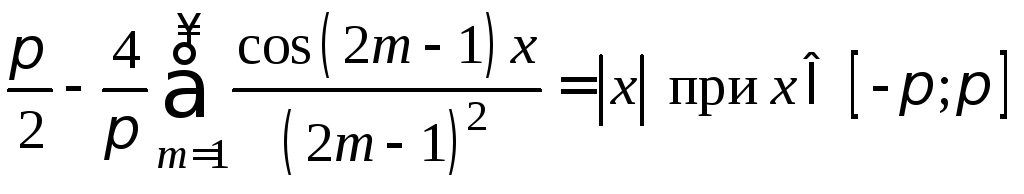 .
.
 или
или .
Откуда снова следует тождество Эйлера.
Действительно, если обозначить
.
Откуда снова следует тождество Эйлера.
Действительно, если обозначить ,
то увидим, что
,
то увидим, что или
или .
. или
или .
Если обозначить
.
Если обозначить ,
то получим
,
то получим (Эйлер).
(Эйлер).