§4. Предельный переход и арифметические операции.

Лемма 1.Сумма конечного числа бесконечно малых последовательностей снова − бесконечно малая последовательность.

Доказательство.Достаточно ограничиться случаем двух слагаемых. Пустьи− бесконечно малые последовательности. Если− произвольное положительное число, то для почти всехбудет. Следовательно.

Замечание.Для бесконечного числа слагаемых подобное утверждение не верно.

Контрпример. Если , то− б.м., в то время как.

Лемма 2.Произведение бесконечно малой последовательностии ограниченной последовательностипредставляет собой бесконечно малую последовательность.

Доказательство. По условию, для почти всех, где. Следовательно, для почти всех.

Теорема 1. (О пределе суммы). Еслии, то существует предел последовательностии он равен. Краткая формулировка: предел суммы равен сумме пределов. (Это утверждение справедливо для любого конечного числа слагаемых).

Теорема 2. (О пределе произведения). Еслии, то существует предел последовательностии он равен. Краткая формулировка: предел произведения равен произведению пределов. (Это утверждение справедливо для любого конечного числа сомножителей).

Теорема 3. (О пределе отношения). Еслии, причём, то существует предел последовательностии он равен. Краткая формулировка: предел отношения равен отношению пределов.

Доказательство теоремы 3. Мы имеем, где− б.м. последовательности. Поэтому разностьпредставляет собой произведение б.м. и ограниченной последовательностей (и, следовательно,отделена от нуля, а потому последовательностьограниченна). Таким образом,, где− бесконечно малая последовательность, т.е..

§5. Предел функции. Свойства пределов.

Определение. Числоназывается пределом функции(в записи:), если для любого положительного числав некоторой окрестности точкивыполняется неравенство. С помощью логической символики это можно выразить следующим образом:.

В частности, если здесь , тоназывается б.м. функцией.

Определение. Функцияназывается б.б.(в записи), еслив некоторой окрестности т.выполняется неравенство.

Свойства пределов функций формулируются и доказываются точно так же, как и свойства пределов последовательностей.

Лемма 1. Бесконечно большие и бесконечно малые функциивзаимно обратны по величине.

Лемма 2. Равенствовыполняется тогда и только тогда, когда, где− б.м. функция.

Лемма 3. (Свойство локальной ограниченности) Если существует конечный предел функции, то эта функция ограниченна в некоторой окрестности точки.

Теорема 1. (О предельном переходе в неравенстве). Пустьи. Тогда, если, тов некоторой окрестности точки. Наоборот, еслив окрестности точки, то.

Теорема 2. (О двустороннем ограничении.) Еслив окрестности точкии, то.

Теорема 3. (Предельный переход и арифметические операции) Пустьи. Тогда,. Если дополнительно известно, что,.

§6. Сравнение б.М. (б.Б.) функций. Эквивалентные функции.

Определение. Функциииназываются эквивалентными (в записи:), если.+

Определение.Мы будем писать, если. Если при этом− б.м. функции, то говорят, что− б.м. более высокого порядка, если же обе эти функции б.б., то говорят, что− б.б. более высокого порядка.

Теорема 1. Функциииэквивалентнытогда и только тогда, когда(или, что то же,).

Доказательство. Достаточно заметить, что.

Теорема 2. Если при вычислении предела дроби заменить любойсомножитель (в числителе или в знаменателе) на эквивалентную функцию, то это не повлияет ни на существование, ни на величину предела.

Доказательство. Пустьипри. В таком случае будет

=.

Таблица основных эквивалентностей

(вывод будет дан на одной из ближайших лекций).

При выполнении условия имеют место следующие эквивалентности: 1. 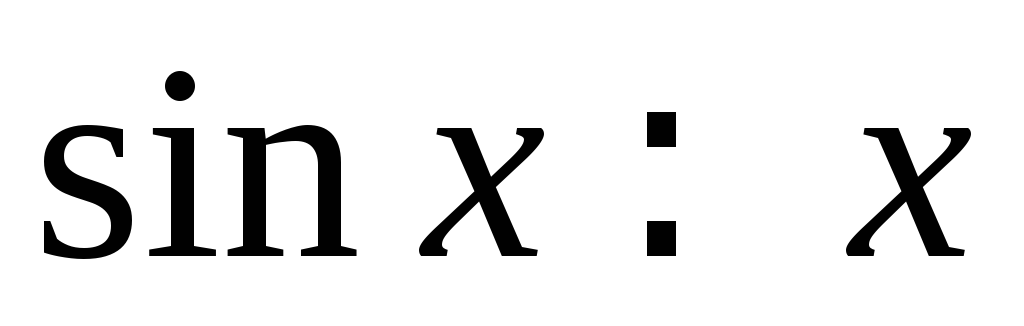; 2.; 3.; 4.; 5. 6. ; 7.; 6’. ; 7’. ; 8. .