§4. Поточечная и равномерная сходимость функциональных рядов.

Определение 1. Функциональный рядсходится в точке, если числовой рядявляется сходящимся. Совокупностьтаких точек (точек сходимости) называетсямножеством сходимости (или областью сходимости) ряда. Говорят ещё, что рядпоточечно сходитсяна множестве. (Отметим, чтоможет быть совершено произвольным подмножеством числовой прямой.)

Пусть − сума,n-я частичная сумма иn-й остаток ряда.. Поточечная сходимость ряда на множествеозначает, чтов каждой точке.

Определение 2. Ряд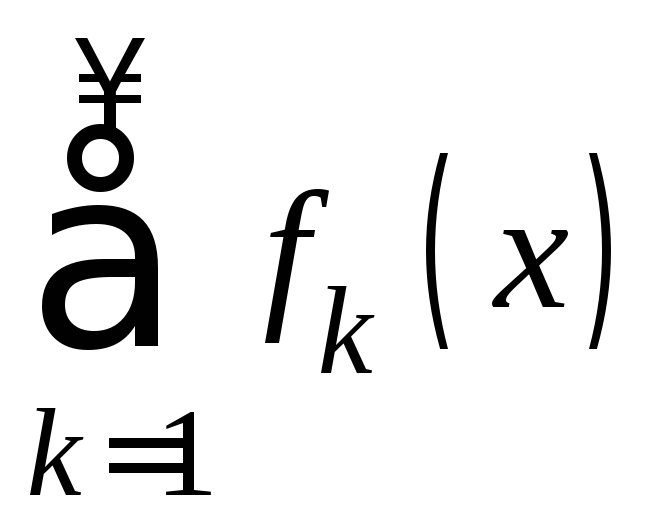равномерно сходится на множестве, если. Это означает другими словами, что последовательность частичных суммравномерно сходитсясумме рядаилиÃ.

Ясно, что из равномерной сходимости следует поточечная сходимость на этом множестве, Обратная импликация не верна.

Контрпример. Рассмотрим на отрезкепоследовательность функцийили ряд .В этом примере. Однако, следовательно,.

Критерий Коши равномерной сходимости ряда. Рядравномерно сходится на множестветогда и только тогда, когда.

Доказательство. Необходимость условия Коши сразу следует из равенства.

Предположим теперь, что условие Коши выполнено. Тогда последовательность поточечно фундаментальна и, следовательно, имеетпоточечный предел, скажем. Кроме того, в силу условия Коши, существуетномертакой, чтобудетвсюду на множестве. Переходя к поточечному пределу, видим, чтовсюдуили. Таким образом,Ã.

Следствие (Признак Вейерштрасса равномерной сходимости ряда). Если функциональный рядправильно сходится на множестве, т.е. мажорируетсяпосредством сходящегося числового ряда, скажем, то данный функциональный ряд равномерно сходится.

Доказательство.Еслии при всех значениях, а рядсходится, то.. Поэтому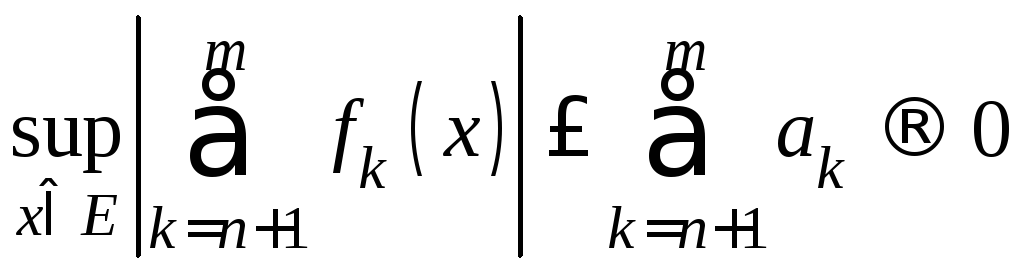. В таком случае согласно критерию Коши рядравномерно сходится на множестве.

Признак Абеля равномерной сходимости ряда. Рассмотрим ряд вида.

Предположим, что выполнены следующие условия:

1. ряд равномерно сходится на множестве,

2. последовательность 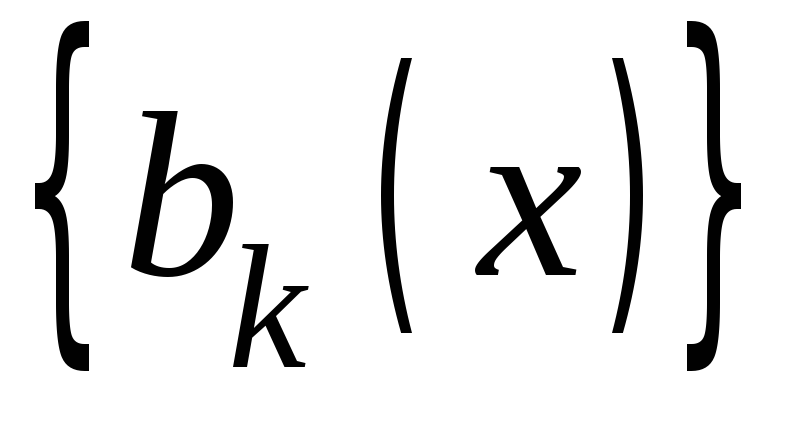равномерно ограничена, т.е. существует такое положительное число, что,

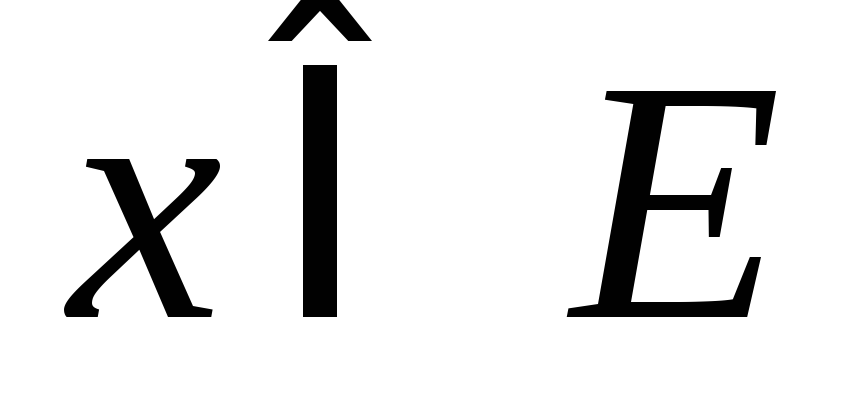
3. при любом фиксированном значении − монотонная последовательность.

В таком случае ряд равномерно сходится на множестве .

Доказательство. Обозначимостаток рядаи. Из условия 1) следует, что, когда. Оценим величину.

.

Поэтому ввиду монотонности последовательности. Следовательно, . Остаётся воспользоваться критерием Коши равномерной сходимости ряда.

§5.Три теоремы о равномерной сходимости.

Теорема 1. (О непрерывности предела последовательности). Если последовательность непрерывных на отрезкефункцийравномерно сходится, тонепрерывна на этом отрезке.

Доказательство. Для любогонайдётся номертакой, что.

По теореме Кантора функция равномерно непрерывна на отрезке, следовательно, существует такое, что для любых, для которых, будет. Поэтомубудет

.

Отсюда следует равномерная непрерывность функции .

Следствие. (О непрерывности суммы ряда).Если все члены ряда непрерывныи ряд равномерно сходится на этом отрезке, то сумма ряда также непрерывна.

Теорема 2. (О почленном интегрировании последовательностей).Если последовательность непрерывных на отрезкефункцийравномерно сходится, то, предел интеграларавен интегралу от предела, точнее,

Ãна отрезке.

Доказательство.Утверждение теоремы следует из оценки

.

Следствие. (О почленном интегрировании рядов). Если все члены ряда непрерывныи ряд равномерно сходится на этом отрезке, то этот ряд можно почленно проинтегрировать по отрезку,.

Теорема 2. (О почленном дифференцировании последовательностей). Пусть выполнены следующие условия:

1. все функции непрерывно дифференцируемы,

2. последовательность функций равномерно сходится,

3. числовая последовательность сходится.

В таком случае последовательность равномерно сходится к функции, при этом, т.е. производная предела равна пределу производной.

Доказательство. Из теоремы 2. и тождестваследует равномерная сходимость последовательностии равенство.

Теорема 1. показывает, что функция непрерывна, поэтому, дифференцируя последнее равенство, видим, чтои что.

Следствие. (О почленном дифференцировании рядов). Рассмотрим функциональный ряд. Пусть все− непрерывно дифференцируемыефункции, пусть ещё ряд из производных равномерно сходится, а сам ряд сходится в точке. В таком случае данный ряд равномерно сходится, его сумма принадлежит классу. Кроме того, этот ряд допускает почленное дифференцирование, т.е. производная суммы ряда равна сумме производных его членов.