15 Свнт и их законы распределения.

1) , где f_x –плотность распределения вероятности (1)

F_x = P{X<x}

Прямая аналогия с дискретным случаем.

Обратное представление:

2) , еслих – точка непрерывности

При таком распределении все скачки сглаживаются.

3) Функция распределения всегда непрерывна у свнт.

4) Р{x₁ ≤ Х ≤x₂}=F_x(x₂)- F_x(x₁)= Р{x₁ ≤ Х ≤x₂} (3)

5) Р{x ≤ Х ≤ x+x}=F_x(x+x)- F_x(x)= F_x(x)=F’_x(x)x+0(x)перейдем к дифференциалам  Р{x ≤ Х ≤ x+dx}= F’_x(x)= f_x(x)dx – вероятность попасть на участок dx.

Определение: f_x(x)dx- называется элементом вероятности.

16 Числовые характеристики свнт.

1. Моменты:

1. начальные: (сумма заменяется на интеграл);

б) центральные: .

Частные случаи.

M_x=₁,

₀=1, ₁=0;

Ремарка: Данные характеристики существуют тогда и только тогда, когда данные несобственные интегралы сходятся.

D_x=₁=₂-m_x².

2. Мода: - точка на осих, соответствует максимальной плотности, если она принадлежит Е_х.

3. Медиана: Присуща только непрерывным случайным величинам.

h_x – точка на оси х, для которой вероятность оказаться левее равна вероятности оказаться правее, т.е. Р{Х < h_x}= Р{Х > h_x}

Р{Х < x₀}=0 для любого случая..

Если перейдем к функции распределения, то заметим, что hx – корень уравнения .

Определение: Данные характеристики называются характеристиками положения. Совпадают только в симметричном случае.

17 Основные классические распределения непрерывного типа и их характеристики.

1. Равномерное распределение.

f_x=0, при и f_x=,

f_x(х)

a b x

Условия нормировки (обязательное требование к плотности): =1

, ;

Пример: Отчет времени измеряется прибором. Ошибка распределена равномерно между серединами двух соседних линий.

Обозначение: XR(a,b)

2. Показательное (экспериментальное) распределения.

Обозначение: XЕ_х()

f_x=0, при х ≤ 0 или е^-х при х>0;

Пример 1: Модель отказов радиоаппаратуры, приводящая к показательному распределению.

Пусть Х – время безотказной работы радиоаппаратуры. Формализация: пусть известно, что аппаратура проработала х единиц времени без сбоя. Причем, что вероятность отказа радиоаппаратуры за время х, следующее за моментом времени х, пропорциональна х и не зависит от того, сколько времени она проработала без сбоя.

Математика: Р{ Х <x₂+хХ ≥x}=х =(х) (3)

Решение. Ищем закон распределения. РассмотримF_х(х)= F_х(х+х)-F_х(х)=

=Р{ х<Х<х+х}= (используем произведение событий)=(по формуле умножения)==Р{ Х<х+хХ ≥ х}=(1-F(x)) (х+(х))

, .

F_x = 0 для х ≤ 0 . начальное условие F_x = 0.

-ln(1- F_x)= х+C

1- F_x=C₁e^-x, C₁= e^c

F_x=1- C₁e^-x

F_x(0)=1- C₁e^-0=1- C₁=0  C₁=1

F_x(x)=1- e^-x

0, при х ≤ 0

F_x(x)=

1- e^-x, при х>0.

0, при х ≤ 0,

Ответ: f_x = F_x’(x)=

 e^-x, при х>0.

Примеры экспериментов: 1) Время ожидания очереди (массовое обслуживание).

2) Время поиска.

Характеристики экспоненциального распределения:

а) Вычислим

, k=1,2…

, (нормировка).

,

- имеет смысл величины обратной математическому ожиданию.

D_x= .

б) Вычислим медиану h_x для данного распределения.

F_x(x)= , 1-=,=,x=

Распределение Симпсона:

Плотность имеет вид -

18 Нормальное распределение (гаусовское).

Введем обозначения

XN(m,).

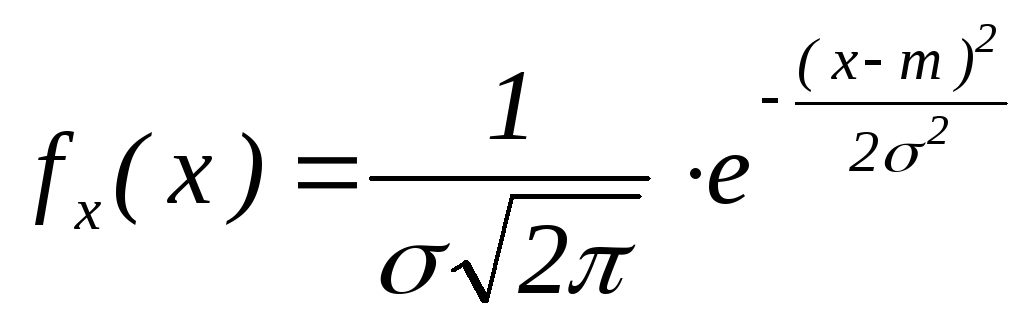,  x  R, m – любое,  >0.

Графически: площадь над гаусовской кривой.

а) Вычислим математическое ожидание.

m_x=

Первый интеграл – интеграл Пуассона и равен , второй интеграл – интеграл от нечетной функции, пределы симметричны интеграл равен 0.

m_x=m.

б)

,

(4)

где k=1,2,3….

.