24 Независимость случайных событий.

Определение: Случайные величины X, Y называются независимыми, если выполняются условия:

F_X,Y(x,y)= F_X(x)F_Y(y) (5)

Теорема 9.1. Для независимости X и Y необходимо и достаточно, чтобы P_{i j} = P_i= P_{ j}

 i, j из основной таблицы распределения

Доказательство: Пусть P_{i j} = P_i= P_{ j}  F_X,Y(x,y)=(согласно задаче 3) = =

== F_X(x)= F_Y(y)

{X<x_i}, {Y<y_j}. Достаточность доказана.

Необходимость. Пусть Х и Y - независимые, т.е. по определению Fx,y(x,y)=F_X(x)F_Y(y), для любых x,y,  R. Пусть (x_i,y_i)  E_X,Y - произвольный дискрет. Выберем столь малые x_i и y_i, чтобы прямоугольник П(x_i,y_i) с центром в этой точке и вершинами ((x_ix_i),(y_i y_i)) не содержал никаких других дискретов, кроме этого.

Pij=(по определению)=P{X=x_i, Y=y_i}=(по построению)=P{X,Y П(x_i,y_i)}=F_X,Y(x_i+x_i , y_i+ y_i)+

+F_X,Y(x_i -x_i , y_i - y_i) - F_X,Y(x_i -x_i , y_i + y_i) -F_X,Y(x_i+x_i , y_i -y_i)== F_X(x_i+x_i) F_Y( y_i+ y_i)+ F_X(x_i -x_i) F_Y( y_i - y_i) - F_X(x_i - x_i) F_Y( y_i+ y_i) - F_X(x_i+x_i) F_Y( y_i - y_i)=

F_Y(y_i-y)(F_X(x_i+x)-F_X(x_i -x)) - F_Y(y_i - y)(F_X(x_i - x) -F_X(x_i -x))=

( F_X(x_i + x)- F_X(x_i - x))( F_Y( y_i+ y_i) - F_Y( y_i - y_i))

П(x_i,y_i)}= ( F_X(x_i + x)- F_X(x_i - x))( F_Y( y_i+ y_i) - F_Y( y_i - y_i))=p_ip_j Теорема доказана.

Примечание. В теореме 9.1 устанавливается так называемое локальное условие независимости случайных величин X и Y. Согласно этому локальному определению независимости, распределение из примера 1 соответствует распределению независимых компонент X и Y.

Определения: случайные величины X и Y рассматриваются как компоненты некоторого вектора, называются независимыми, если функция распределения

F(x,y)=F_x(X)F_y(Y), (расщепляется на произвольные составляющие).

(x,y) R².

Следствие (локальное определение независимости).

Из (1)  (2)

(плотность также должна расшепляться).

Это определение обобщается на вектор  размерности ( количество случайных величин, рассматриваемых в одном и том же вероятностном пространстве).

22 Случайные векторы непрерывного типа (СВНТ) и их законы распределения.

Определение: Двумерный случайный вектор (X,Y) называется двумерным случайным вектором непрерывного типа, если множество типа континуум на плоскости и существует такая непрерывная и интегрируемая по Риману в бесконечных пределах функция f _X,Y(x,y), называемая плотностью распределения вероятности случайного вектора (X,Y) (или плотность совместного распределения компонент) такая, что имеет место равенство:

F_X,Y(x,y)=(1)

Следствия.

1) F_X,Y(x,y) - непрерывная на всей плоскости по двум переменным.

2) f_X,Y

3) (условие нормировки)

(F_X,Y(+,-)=1)

4)

Доказательство. Имеем: F_X,Y(x,+ )=Fx(x)по свойству функции распределения. по формуле (1) следует, что F_X(x)= .Но f_x(x)=(x) (x)=

Свойство доказано.

5)Если (x,y) - точка непрерывности плотности, то f_X,Y=(из (1))

6) Понятие "элемента вероятности" :

f_X,Y(x,y)dxdy=P{(x,y) П(x,y)}

(вероятность попадания в прямоугольник П(x,y))

7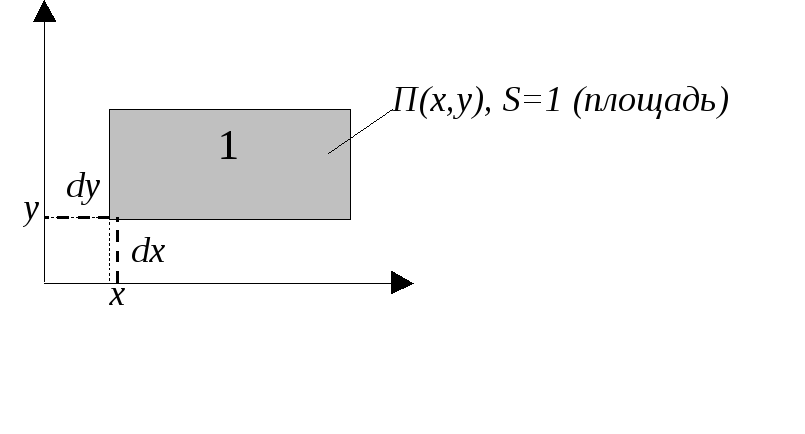) ПустьG-некоторая область на плоскости, тогда вероятность попадания в эту область:

P{(x,y) G}=

Нужно разбить всю плоскость на элементы dxdy и просуммировать.

Числовые характеристики случайного вектора.

1) Момент распределения.

_k,s=

_k,s=

k+s - суммарный порядок момента

	Начальные моменты	Центральные моменты
k+s=0	0,0	0,0=1
k+s=1	1,0===|Pij=Pi|==mx 0,1=mx	1,0=0
	0,1==| рассуждаем аналогично|= my 0,1= my	0,1=0
k+s=2	2,0=M[X2]	2,0=Dx
	0,2=M[Y2]	0,2=Dy
	1,1=M[XY]	1,1=Cov(X,Y) - ковариация 1,1= Cov(X,Y)=KX,Y X,Y=-нормированная ковариация или коэффициент корреляции

2) Вычислить коэффициент корреляции для примера 1.

Решение. Из первой таблицы следует:

m_X=; m_Y=;

_1,1;_1,1= _1,1 - m_X m_Y

Пример 2. Пусть Х_1, Х₂,…Х_n – независимы и X_kN(m_k,_k).

Построить плотность совместного распределения компонент вектора Х=(х₁,х₂…х_n).

Решение. В силу (2) для общего случая n-мерного вектора:

, 

-

плотность n-мерного распределения с независимыми компонентами.

Замечание. Если X и Y – нормальны, но зависимы, то плотность вектора (X,Y) записывается следующим образом: где С – нормировочная константа;

Q – неотрицательная определенная квадратичная форма двух переменных.