
- •1 Вводные понятия
- •2 Алгебра событий
- •5 Аксиомы теории вероятностей и следствия из них
- •3 Формула классической вероятности (схема урн)
- •4 Схема геометрической вероятности.
- •6 Формула сложения вероятностей.
- •7 Условные вероятности. Независимость событий.
- •Вероятность осуществления b при условии, что произошло a в том же эксперименте, определяется через отношение двух безусловных вероятностей.
- •8 Зависимые и независимые события
- •9 Правила вычисления вероятностей сложных событий.
- •10 Последовательность независимых испытаний. Схема Бернулли.
- •11 Случайные величины
- •Функция распределения случайно величины и ее свойства.
- •12 Закон распределения случайной величины дискретного типа.
- •13 I. Равномерное распределение (дискретное)
- •II. Биномиальное распределение
- •III. Распределение Пуассона
- •IV. Геометрическое распределение
- •14 Пуасоновское распределение как предельный случай биномиального.
- •15 Свнт и их законы распределения.
- •3) Функция распределения всегда непрерывна у свнт.
- •16 Числовые характеристики свнт.
- •Если перейдем к функции распределения, то заметим, что hx – корень уравнения .
- •17 Основные классические распределения непрерывного типа и их характеристики.
- •19 Интеграл вероятности и его свойства
- •20 Случайные векторы
- •Свойства двумерной функции распределения.
- •21 Случайные векторы дискретного типа (свдт) и их законы распределения.
- •24 Независимость случайных событий.
- •23 Вероятность попадания в область на плоскости
- •25 Функция от случайных величин. Теоремы о мат. Ожидании функций.
- •26 Свойства числовых характеристик случайного вектора.
- •Следствия из свойства 5.
- •Доказать, что если 4, то автоматически существует 1, 2, 3, используя неравенство Коши-Буняковского.
- •Пусть Перейдем от(X,y) к(u,V)путем преобразования стандартизациирассмотрим
- •28 Законы распределения функций
- •31 Законы больших чисел.
- •Неравенства Чебышева. Первое неравенство Чебышева.
- •При увеличении числа опытов по схеме Бернулли относительная частота успехов
- •32 Центральная предельная теорема.
- •33 Следствия цпт для схемы Бернулли.
- •34 Основные понятия математической статистики.
3 Формула классической вероятности (схема урн)
Пусть выполнены два условия:
Ω =1, 2,…, n (множество - конечное)
P(1)=P(2)=…= P(n) ( исходы равновероятны)
Тогда справедлива формула классической вероятности:
![]() ,
где
,
где
![]() - число элементовА,
- число элементовА,
![]() - число элементовΩ.
- число элементовΩ.
![]()
В силу конечности , алгебра F - система всех подмножеств из - является алгеброй любое подмножество из - наблюдаемое событие. Тогда А =k1, k2,…, km, /А/=m
![]() Т.к.
Ω =1+2+…+n
(по аксиомам
2,3)
1=Р(1)+Р(2)+Р(n)=рn,
где p=p(k),
k=1,2,..,n
p=1/n P(A)=
Т.к.
Ω =1+2+…+n
(по аксиомам
2,3)
1=Р(1)+Р(2)+Р(n)=рn,
где p=p(k),
k=1,2,..,n
p=1/n P(A)=![]() =
=![]()
![]()
Пример 1. Из колоды в 36 карт наудачу извлекаем одну карту. Найти вероятность события С=появится картинка или карта красной масти.
![]() Логика
=>
Алгебра =>
правила исчисления вероятности сложных
событий. Ключевым является слово
“наудачу”,
что оправдывает применение схемы
классической вероятности => C=A+B,
где
А=появится
картинка,
В=появится
карта красной масти.
Логика
=>
Алгебра =>
правила исчисления вероятности сложных
событий. Ключевым является слово
“наудачу”,
что оправдывает применение схемы
классической вероятности => C=A+B,
где
А=появится
картинка,
В=появится
карта красной масти.
По
Ф.С.В.(2)
P(C)=P(A)+P(B)-P(AB)=![]() .
.![]()
4 Схема геометрической вероятности.
Распространим классическую схему на случай, когда Ω – непрерывно (континуум). Пусть Э. (эксперимент) удовлетворяет следующим условиям:
Ω – квадрируемая область (имеет площадь) на плоскости;
А Ω – любая квадрируемая подобласть из Ω;
Эксперимент состоит в выборе наудачу точки из Ω (т.е. вероятность попадания в любую подобласть из Ω не зависит от ее расположения, а только от ее размера) справедлива формула геометрической вероятности:
 (6)
(6)
Заметим, что квадрируемость понимается как площадь в смысле меры Лебега, а не меры Римана.
Обобщение
Ф.Г.В. на случай евклидова пространства
Rn:
![]() (7)
(7)
Пример
2. Задача
о встрече (на семинаре). ![]() См задачу 14.148, 14.149
в [
]
См задачу 14.148, 14.149
в [
]
![]()
Пример 3. Задача Бюффона.
На плоскость, разграниченную параллельными прямыми линиями на расстоянии 2а друг от друга, наудачу бросается игла диной 2l (l<<a). Найти вероятность следующего события А=игла пересечет какую-либо из параллельных прямых линий.
![]() Будем
описывать положение иглы двумя
координатами:
- угол, y
– расстояние до ближайшей прямой.
Будем
описывать положение иглы двумя
координатами:
- угол, y
– расстояние до ближайшей прямой.
(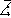 ,y)
– положение
иглы по
отношению к ближайшей прямой.
,y)
– положение
иглы по
отношению к ближайшей прямой.
Ω
= (,y
)
0![]()
![]() ,
0
,
0![]() у
у![]() а
а
А
= (,y
)
0
![]() у
у![]() lsin;
0
lsin;
0![]()
![]() }
}
![]()
Если
l=a/2
P(A)=1/
![]()
6 Формула сложения вероятностей.
Для А,В: Р(А+В)=Р(А)+Р(В)-Р(АВ) (2)
![]() A+B=(A+B)Ω=(А+В)(А+
A+B=(A+B)Ω=(А+В)(А+![]() )=A+A
)=A+A![]() +AB+B
+AB+B![]() =A+AB+B
=A+AB+B![]() =A+B
=A+B![]() P(A+B)=P(A)+P(B
P(A+B)=P(A)+P(B![]() )
(3)
)
(3)
По
формуле (1):
B=AB+B![]()
(по аксиоме
3)
P(B)=P(AB)+P(B
(по аксиоме
3)
P(B)=P(AB)+P(B![]() ).
).
Подставим
в формулу (3): Р(В![]() )=P(B)-P(AB)
P(A+B)=P(A)+P(B)-P(AB)
)=P(B)-P(AB)
P(A+B)=P(A)+P(B)-P(AB)
В частном случае, когда А,В - несовместны => P(AB)=0 => аксиома аддитивности.
6) Формула сложения для 3-х событий.
P(A+B+C)=P((A+B)+C)=P(A+B)+P(C)-P((A+B)C)=P(A)+P(B)-P(AB)+P(C)-(P(AC)+P(BC)-P(ABC))=
=P(A)+P(B)+P(C)-P(AB)-P(BC)-P(AC)+P(ABC)
P(A+B+C)=P(A)+P(B)+P(C)-P(AB)-P(BC)-P(AC)+P(ABC) (4)
7) Для А1, А2,….,Аn :
![]() =
=![]() (5)
(5)
Задача
(о рассеянной секретарше):Даноnписем иnконвертов.Cекретарша
все перепутала и отослала
наудачу. Какова вероятность, что хотя
бы один из адресатов получит свое письмо?
![]() См. задачу №14.221 в[]
См. задачу №14.221 в[]
![]()
7 Условные вероятности. Независимость событий.
Аксиома
4. ![]() ,
P(A)
0. (1)
,
P(A)
0. (1)
