Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Рязанский государственный радиотехнический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

For Exam / Приложения определенного интеграла

.pdf

Скачиваний:

Добавлен:

15.04.2015

Размер:

338.66 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

§ 9. ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА

Все подынтегральные функции, встречающиеся в этом параграфе, предполагаются непрерывными.

9.1. Вычисление площади плоской фигуры

Вычисление площадей плоских фигур основано на геометрическом смысле определенного интеграла. Площадь

криволинейной трапеции, ограниченной сверху графиком функции y f x f x 0 , слева и справа - соответственно прямыми x a и x b, снизу – отрезком a,b оси Ox (см. рис.9.1),

					b
вычисляется по формуле				S f x dx.		(9.1)
					a
Если	f x 0при x a,b (см. рис. 9.2), то
				b
			S f x dx.			(9.2)
y			y	a
y			y		a		b
		y=f(x)	O				x
							x

						S
						S

		S			y f x

O	a Рис.9.1 b		x
O	a Рис.9.1 b		x			Рис. 9.2

Формулы (9.1) и (9.2) можно объединить в одну:

b					y
S	f x	dx .		(9.3)
S	f x	dx .		(9.3)
a
Если		плоская		фигура
ограничена				кривыми
y f1 x		и		y f2 x ,
y f1 x		и		y f2 x ,
причем		x a	f1 x f2 x ,
прямыми		x a	и	x b (см.	O	a

y=f2(x)

y=f1(x)

b x

Рис.9.3

рис. 9.3), то ее площадь			y
находится по формуле			y
b			d
S f2 x f1 x dx.		(9.4)			y= (x)
a				S
Пусть	криволинейная			S
Пусть	криволинейная
трапеция	ограничена	кривой	с
x y ,	прямыми	y c и

y d и отрезком c,d оси Oy O				Рис. 9.4			x
(см. рис 9.4). Тогда площадь				Рис. 9.4
(см. рис 9.4). Тогда площадь
этой трапеции вычисляется		по
формуле
d
S y dy.	(9.5)
c
Если криволинейная трапеция ограничена сверху кривой,
заданной параметрическими уравнениями
	x x t ,	y t	0,	t t ,t	2	,
				1	2
	y y t ,
прямыми x a и	x b и отрезком a,b оси Ox , то ее площадь
вычисляется по формуле		t2
		t2					(9.6)
		S y t x		t dt ,			(9.6)
		t1

где t1 и t2 определяются из уравнений: x t1 a и x t2 b.

Предполагается,		что на	отрезке	t1,t2 функции			y t и
Предполагается,		что на	отрезке	t1,t2 функции			y t и	x t
непрерывны.
Площадь						r=r( )
криволинейного		сектора,
					S

ограниченного		кривой,
ограниченного		кривой,
заданной	в	полярных
координатах	уравнением
r r и двумя лучами
и			O		Рис. 9.5

(см. рис. 9.5), вычисляется по формуле

	1
S		r2 d .		(9.7)

2
Пример			1.9.	Найти
площадь			фигуры,
ограниченной			параболой
y x2 1		и	прямыми	x 0,

x 2 и y 0.

Решение

Сделаем чертеж заданной фигуры (см. рис. 9.6). Так как y x2 1 0 на

1
O	2	x
	Рис.9. 6

сегменте 0,2 , то для вычисления площади применяем формулу

(9.1):

2			x3			2	8	14
						2

S x	2	1dx			x
S x		1dx			x			2 .
0				3		0	3	3
						0

Пример 2.9. Найти площадь фигуры, ограниченной параболой y x2 2x и прямой y x 2 (см. рис. 9.7).

Решение

Найдем абсциссы точек y пересечения данных линий:

x2 2x x 2 x2 x 2 0

x1 2, x2 1.

На отрезке 2,1

x 2 x2 2x, следовательно, по формуле (9.4)

S x 2 x2 2x dx

-2	O	x
Рис. 9.7

	2						1
1	2		x	3	x	2		1	1	8	9
1				3		2

2 x x dx		2x
2 x x dx		2x						2	2	4 2 .
2			3 2				2	3	2	3	2
							2

Пример 3.9. Найти площадь фигуры, ограниченной эллипсом

	x2		y2	1 (см. рис. 9.8).			y
9
		4					2
		Решение. Оси координат
совпадают					с	осями
симметрии заданного эллипса
и делят его на четыре равные								x
части. Таким					образом, для -3		3
нахождения					искомой		-2
площади				достаточно		найти

площадь части фигуры,							Рис. 9.8

расположенной в первой четверти ( x 0, y 0), и умножить

полученный результат на четыре.
Параметрические				уравнения
эллипса имеют вид:
x 3cost ,			y 2sint, t 0,2 . Найдем пределы изменения
переменной t:
0 x 3,			x 0 3cost 0 t					,
0 x 3,			x 0 3cost 0 t					,
							2
			x 3 3cost 3 сost 1 t 0.
Применим формулу (9.6):
	0			0
S 4	0			0	2	tdt	2
S 4	2sint 3cost dt 24 sin					tdt	12 1 cos2t dt
							0
	2			2
		sin 2t
		sin 2t	2
12 t			6 6sin 6 .
12 t			6 6sin 6 .
	2		0
	2		0

*Пример 4.9. Найти площадь фигуры, ограниченной линиями, заданными уравнениями:

x 4
x 4		2cos3 t,	x 2	x 2 (см. рис. 9.9).
			x 2	x 2 (см. рис. 9.9).
y	2sin3 t,

Решение


Для	вычисления			площади		2	y
воспользуемся			симмет-рией
фигуры		относи-тельно			оси			4	2
Ox . Сначала найдем пределы
								x
интегри-рования:							2

2 x 4 2 ,

Рис. 9.9

x 2 4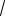2cos3 t 2 cost 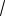2 t , 2 4

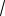x 42 4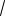2cos3 t 4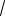2 cost 1 t 0.

Для нахождения половины площади заданной фигуры применим формулу (9.6):

S 2 0 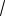2sin3 t 4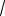2cos3 t dt 24 0sin4 tcos2 tdt


		4																	4
										3																3			4
4											4																		4
6 sin		2 tsin2					2tdt				1 cos2t			1 cos4t dt														1
6 sin		2 tsin2					2tdt		2		1 cos2t			1 cos4t dt														1
0									2		0													2			0
cos2t cos4t cos2t cos4t dt														3	t			4			3sin 2t						4
														3				4			3sin 2t						4

														2			0		4						0
														2			0		4						0
	3sin 4t				3										3					3			sin6t						4
			4				4																						4
							cos6t cos2t dt
							cos6t cos2t dt
8			0		4		0									8			4					8				0
8			0		4		0									8			4					8				0
	3sin 2t					3		3	1		3		3 4
	3sin 2t			4		3		3	1		3		3 4
																.
																.
8				0	8			4	8		8	8
8				0	8			4	8		8	8
	Пример						5.9.			Найти
площадь								фигуры,
площадь								фигуры,																					6
ограниченной																													6
ограниченной
“трехлепестковой									розой”
r sin3 (см. рис. 9.10).
	Решение.					По		формуле														Рис. 9.10
(9.7) найдем					шестую					часть												Рис. 9.10
(9.7) найдем					шестую					часть

искомой площади. Она за-

крашена на рисунке. Окончательно площадь “розы”:

			1
S			1	6	sin2 3 d
	6
	6
			2	0
	3					3			sin 6		6
		6					6				6
			1 cos6 d										.
			1 cos6 d										.
	2	0			2		0	4		0		4
	2	0			2		0	4		0		4

9. 2. Вычисление длины дуги кривой
Пусть кривая на плоскости задана уравнением	y f x , где
f x - непрерывно дифференцируемая функция	для всех x:
a x b. Тогда длина l дуги кривой, заключенной между

точками с абсциссами, равными a и b , вычисляется по формуле:

b
	1 f	2
l			(9.8)
		x dx.

В случае задания кривой уравнением x y , где c y d ,

длина l дуги кривой, заключенной между точками с ординатами равными, c и d , вычисляется по формуле:

d
		2
l			(9.9)
	1	y dy.

Если кривая задана параметрическими уравнениями

x x t ,	y t 0,	t t ,t	2	,
		1	2
y y t ,

где x t и y t - непрерывные вместе со своими производными функции и x t1 a, x t2 b, то длина дуги кривой находится по формуле:

		t2
	l				2		2	(9.10)

				x	t y t dt.
Пусть	кривая задана	t1	уравнением			в	полярных координатах

r r ,	.		Предполагаем,				что r
								и r

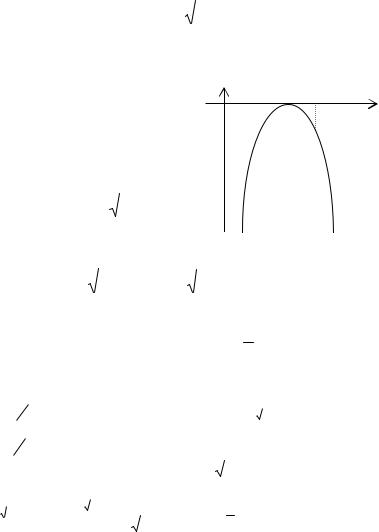
непрерывны на сегменте , . В этом случае длина кривой вычисляется по формуле:

d .

(9.11)

Пример 6.9. Вычислить длину дуги кривой y lnsin x от

до x2

(см. рис. 9.11).

Решение.

Изобразим

часть

графика

заданной

функции

приО

x 0, .

Воспользуемся

формулой (9.8).

Прежде чем записать интеграл,

найдем выражение

1 f

Рис. 9.11

f x lnsin x, f x

cosx

ctgx,

sinx

1 f

1 ctg

sinx

Для

вычисления

интеграла

используем

универсальную

тригонометрическую подстановку t tg x :

t tg

x 2arctgt

sin x

2dt

1 t2

3 dt

ln 3


sin x			2t
sin x
		1 t2					2dt
						3	2dt
t			1
t			1				1 t2	2t
	2				1			2t
	2				1
2								1 t	2
2									2
t				3
t				3
3

ln1 ln 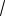3.

	1			6
	x	t				,

Пример 7.9. Найти длину кривой	6		1			между

y 2					t4,
		4

точками пересечения ее с осями координат.

Решение. Найдем параметры точек пересечения с осями Ox и

Oy:

с осью Oy - x 0 t 0,

								y 0						2		1	t4	0							t 4				.
			с осью Ox				-									1												8
			с осью Ox				-																					8
															4
			Тогда по формуле (9.10) длина дуги равна:

		4						2				1			2			4
			8					2												8
																							2							2
					1																		2							2
l						t6					2		t4		dt							t5				t3					dt
l						t6					2		t4		dt							t5				t3					dt
		0		6								4						0

																													4
																											3			8
																														8

	4 8									4 8											2			4		1
	4 8								1	4 8		t4 1d t4 1							1				t	4
	t3				t4 1dt				1										1				t
	t3				t4 1dt
	0							4		0								4							3				0
																													0

1 27 1 13.

6 3


	Пример 8.9. Найти длину дуги кривой r 6sin , 0										.
	Пример 8.9. Найти длину дуги кривой r 6sin , 0										.
										3
	Решение. Для вычислений воспользуемся формулой (9.11):

					2
	3	2				3
l	3	2				3	sin	2	2	d
l		6sin		6sin		d 6	sin		cos	d

	0					0
	0					0

	3		3	2 .
6 d 6				2 .
	0		0
			0

9. 3. Объем тела

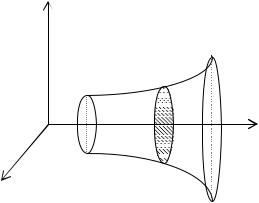
1.Вычисление объема тела по известным площадям поперечных сечений

Пусть в пространстве задано тело и построены его сечения плоскостями, параллельными оси Ox и проходящими через точки x a,b на ней (см. рис. 9.12). Площадь фигуры в сечении зависит от точки x, определяющей площадь сечения. Если эта зависимость известна и задана непрерывной на a,b функцией S x , то объем

тела, заключенного между плоскостями			x a и	x b,
вычисляется по формуле:
	b
	V S x dx.			(9.12)
	a
y		S(x)
y		S(x)

O a

b x

zРис. 9.12

2.Объем тела вращения

Если тело образовано вращением криволинейной трапеции,

ограниченной кривой y f x		f x 0	и прямыми	y 0,
x a и x b, вокруг	оси Ox	(см. рис.	9.13), то его	объем
	b	f x 2 dx.
вычисляется по формуле:	V	f x 2 dx.	(9.13)

	y
	y=f(x)
	O
	O
	a					x
z		x			b


	Рис. 9.13
	Рис. 9.13
Если тело образовано вращением					криволинейной трапеции,
ограниченной	кривыми	y f1 x ,				y f2 x ,		где
f2 x f1 x 0, и прямыми		x a		и	x b, вокруг оси Ox , то
его объем вычисляется по формуле:					f1 x 2 dx.
	b
	V f2 x 2							(9.14)
	a
Если тело образовано вращением					криволинейной трапеции,
ограниченной	кривой x y		y 0			и	прямыми	x 0,
y c и y d , вокруг оси		Oy,	то его объем				вычисляется по

формуле:

V y 2 dy. (9.15)

Пример 9.9. Найти объем тела, ограниченного эллиптическим

параболоидом x	y2	z2
			и плоскостью x 2 (см. рис. 14).
	2	4

Решение

Любое сечение эллиптического параболоида плоскостью, перпендикулярной к оси Ox 0 x 2 , есть эллипс, уравнение

1 / 21 2 > Следующая >>>

Соседние файлы в папке For Exam

#
15.04.2015222.26 Кб18Методы интегрирования подстановкой и по частям.pdf
#
15.04.2015224.95 Кб24Несобственные интегралы 2.pdf
#
15.04.2015216.84 Кб19Несобственные интегралы.pdf
#
15.04.2015203.21 Кб17Определенный интеграл.pdf
#
15.04.2015368.26 Кб18Определители.pdf
#
15.04.2015338.66 Кб21Приложения определенного интеграла.pdf
#
15.04.2015324.83 Кб21Прямая и плоскость в пространстве 1.pdf
#
15.04.2015205.01 Кб23Прямая и плоскость в пространстве 2.pdf
#
15.04.2015414.48 Кб40Прямая на плоскости и кривые второго порядка.pdf
#
15.04.2015269.87 Кб19Решение СЛАУ.pdf
#
15.04.2015434.68 Кб28Тройные интегралы 2.pdf