For Exam / Решение СЛАУ

Исследование систем и их решение методом Гаусса Основные теоретические сведения

Арифметический вектор (вектор-строка) a x;y;z называется ненулевым, если x2 y2 z2 0.

Вектор a 0;0;0 называется нулевым.

Элементарными преобразованиями матрицы называются следующие преобразования:

-перестановка строк матрицы;

-умножение строки на некоторое число;

-прибавление к некоторой строке матрицы другой (других), умноженной (умноженных) на некоторое число (числа).

элементарных преобразований можно привести к ступенчатому виду

Определение. Рангом матрицы A называется число ненулевых строк

совместна (имеет решение) тогда и только тогда, когда ранг расширенной матрицы A СЛАУ равен рангу основной матрицы A rgA rgA .

При этом, если

а) rgA rgA n, то СЛАУ имеет единственное решение;

б) rgA rgA k n, то СЛАУ имеет бесконечно много решений;

Решение. Выполним элементарные преобразования над строками матрицы так, чтобы последовательно получились нули в первом, втором и т.д. столбцах матрицы

Получена ступенчатая матрица с двумя ненулевыми строками. Поэтомуее ранг, а значит, и ранг исходной матрицы равны 2.

В процессе получения ступенчатой матрицы выполнены следующие элементарные преобразования:

-на первом шаге переставлены местами 1-я и 2-я строки;

-на втором шаге ко второй строке прибавлена первая, умноженная на 2; к четвертой строке прибавлена первая.

Врезультате получены нули во втором столбце;

-на третьем шаге к третьей строке прибавлена вторая, умноженная на (-1) (из третьей строки вычтена вторая).

Пример 6.2. Исследовать СЛАУ на совместность и если она

совместна, то найти ее решение:

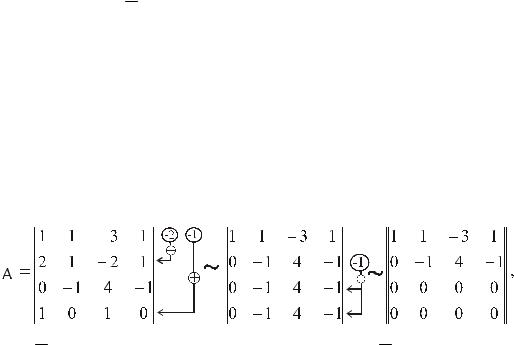
1)из элементов второй строки матрицы В вычитались соответствующие элементы первой строки, умноженные на 2;

2)из элементов третьей и четвертой строк вычитались элементы первой строки, умноженные на 1, и т.д.

Очевидно, что rg A = 4,rg(A) = 3. В соответствии с теоремой Кронекера-Капелли получаем, что система несовместна.

Пример 6.4. Исследовать СЛАУ на совместность и, если она совместна, то найти её решение

x1 x2 3x3 1,

2x1 x2 2x3 1,x2 4x3 1,

x1 x3 0.

Решение:

откуда rgA rgA 2 3. Поскольку ранги матриц А и A равны и равны 2, но

2<3 – числа неизвестных, то СЛАУ имеет бесконечное множество решений. Для нахождения этих решений запишем СЛАУ, равносильную исходной:

x1 x2 3x3 1,x2 4x3 1.

Объявляем x3 свободной переменной (x3= , R) и вместе с коэффициентами при ней переносим в правую часть: