For Exam / Тройные интегралы 2

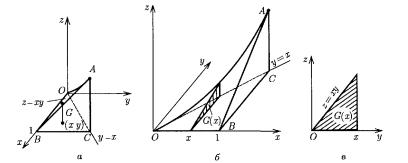
1) Дан тройной интеграл f (x, y, z)dx dy dz , где T –

T

область, ограниченная плоскостями z=0, z=xy, y=x, x =1. Свести данный интеграл к повторному двумя способами:

а) так, чтобы внутренний интеграл был определенным интегралом с переменной интегрирования z;

б) так, чтобы внутренний интеграл был двойным с переменными интегрирования y и z.

В каждом случае свести тройной интеграл к последовательному вычислению трех определенных интегралов.

а) Область Т представляет собой «криволинейную пирамиду» AOBC (рисунок 1,а), основанием которой является треугольник OBC

Рисунок 1

в плоскости (x,y) (обозначим этот треугольник G). Для каждой точки (x,y) области G переменная z изменяется от 0 (значение z в области G) до xy (значение z на

поверхности z = xy), т.е. область Т можно представить в виде:

T { x, y, z x, y G,0 z xy}

По формуле (1) имеем:

Сводя двойной интеграл по области G к повторному, получим:

б) Область Т заключена между плоскостями x=0 и x=1. Сечение области Т плоскостью x=const (рисунок 1,б) представляет собой треугольник G(x). Проекция этого треугольника на плоскость Oyz изображена на рисунке 1,в. По формуле (2) имеем:

1

I dx f x, y, z dy dz

0 G ( x)

Сводя двойной интеграл по области G(x) к повторному, получим:

что совпадает с равенством (9).

2) Вычислить тройной интеграл

I xy z dx dy dz ,

T

где Т – область, ограниченная поверхностями

z = 0, z = y, y = x2, y = 1.

Область Т изображена на

Рисунок 2 рисунке 2. Ее можно представить в виде:

где G = {(x,y): -1 ≤ x ≤ 1, x2 ≤ y ≤ 1}. Сводя тройной интеграл к повторному получим:

T

если область Т ограничена поверхностями z = 0 и (z - 1)2 = x2 + y2 .

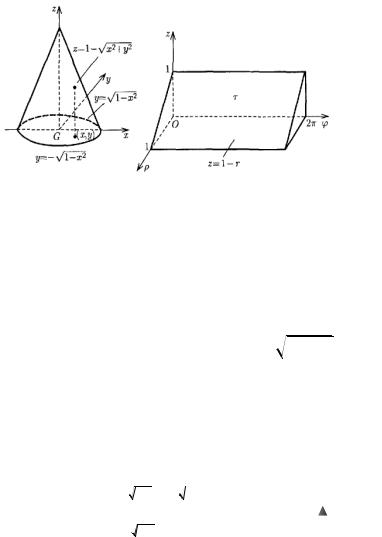
Рисунок 3

Область Т представляет собой конус (рисунок 3). Уравнение конической поверхности, ограничивающей

T x, y, z : x, y G, 0 z 1 x2 y2 ,

где G – круг радиуса 1 с центром в начале координат. Поэтому данный тройной интеграл можно свести к вычислению трех определѐнных интегралов в прямоугольных координатах:

4) Вычислить интеграл

где T – область, ограниченная поверхность x2 y2 z2 z .

Рисунок 4

Область Т представляет собой шар, ограниченный сферой, уравнение которой удобно записать в виде x2 y2 (z 1/ 2)2 1/ 4 (рисунок 4, а). Данный тройной интеграл можно вычислить с помощью повторного интегрирования в прямоугольных координатах:

Однако удобнее перейти к сферическим координатам

(r, ,)

x r sin cos , y r sin sin , z r sin , (10)

причем переменная φ изменяется от 0 до 2π, а при каждом значении φ переменная изменяет от 0 до π/2. Подставляя

являющуюся прообразом области Т при отображении (10). Якобиан отображения (10) равен r2 sin , а подынтегральная функция в сферических координатах равна r. Вычисляя тройной интеграл по области τ с помощью повторного интегрирования, получаем:

Отметим, что расстановку пределов интегрирования для переменной r можно произвести, рассматривая не область, а изменение r при фиксированных значениях и в области Т. Наглядно видно , что на каждом луче const ,const переменная r изменяется в шаре Т от 0 (значение r в начале координат) до cos (значение r на сфере).