
For Exam / Определители
.pdf
17
Определители. Решение систем линейных алгебраических уравнений по правилу Крамера
Основные теоретические сведения I. Определители
Определение 1. Определителем второго порядка, отвечающим
матрице
a |
11 |
a |
12 |
|
, |
A |
|
|
|||
|
|
a22 |
|
|
|
a21 |
|
|
|||
называется число, которое обозначается |
|
A |
|
, det A, |
|
a11 |
a12 |
|
и которое |
|
|
|
|
||||||
|
|
|
|||||||
|
|
|
a21 |
a22 |
|
||||
|
|
|
|
|
|
|
|
равно произведению элементов на главной диагонали матрицы минус произведение элементов на побочной диагонали:.
|
|
|
|
|
|
a11 |
|
a12 |
|
|
a11a22 a12a21 |
(1.1) |
|||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
2 |
|
|
a21 |
|
a22 |
|
|
|
|
|
|
|
|
|
Например, |
|
3 |
|
= 3 5 ( 2) 4 23. |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
4 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определение 2. Определителем третьего порядка, отвечающим |
|
||||||||||||||||
матрице |
|
|
|
|
|
a |
|
|
|
a |
|
a |
|
|
|
||
|
|
|
|
|
|
|
|
11 |
12 |
13 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
A |
a |
21 |
a22 |
a23 |
, |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
a32 |
|
|
|
|
|
называется число, равное |
|
a31 |
a33 |
|
|||||||||||||
|
a11 |
|
|
|
a12 |
|
a13 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
a21 |
|
|
|
a22 |
|
a23 |
|
|
|
|
|
|
|
|
|
|
|
a31 |
|
|
|
a32 |
|
a33 |
|
|
|
a11a22a33 |
a12a23a31 a13a21a32 |
a13a22a31 |
a12a21a33 a11a23a32. |
(1.2) |
|||||||||||||
Запомнить формулу (1.2) легко в виде так называемых «правила треугольнков» или «правила Саррюса».
Правило треугольников. Определитель A матрицы третьего порядка равен
сумме произведений элементов, стоящих на главной диагонали и в вершинах треугольников с основаниями, параллельными главной диагонали
18
минус произведения элементов, стоящих на побочной диагонали и в вершинах треугольников с основаниями, параллельными побочной диагонали (см. рис.1). На рис.1 «кружочками» обозначены соответствующие элементы определителя.
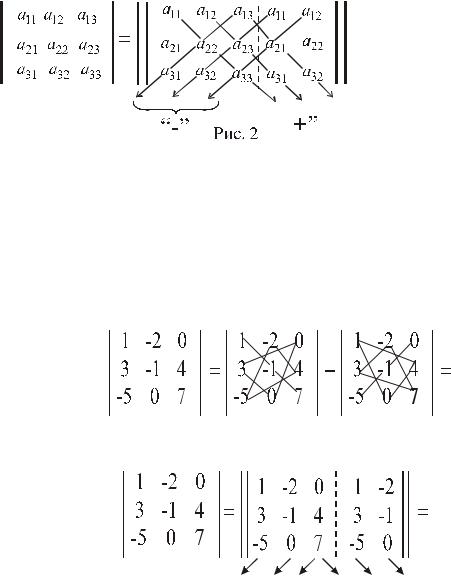
Правило Саррюса. В соответствии с правилом Саррюса из матрицы А нужно составить новую
матрицу, приписав справа к
матрице А сначала первый, а
потом второй её столбцы. Затем
нужно перемножить элементы
новой матрицы в соответствии
 со схемой, приведённой на
со схемой, приведённой на
рис.2.
Элементы новой матрицы перемножаются в направлении стрелок. Полученные произведения берутся со знаками «+» в направлении главной диагонали матрицы А и со знаком «-» в направлении побочной диагонали.
|
|
|
1 |
2 |
0 |
|
|
|
|
|
|||||
Пример 1.1. Вычислить определитель |
|
3 |
1 |
4 |
|
|
|
|
|
|
5 |
0 |
7 |
|
|
а) по правилу треугольников; |
б) по правилуСаррюса. |
||||||
Решение. |
|
|
|
|
|
|
|
а) |
|
|
|
|
|
|
|
=1·(-1)·7+(-2)·4·(-5)+0·3·0-(0·(-1)·(-5)+(-2)·3·7+1·4·0)=-7+40+0-(0-42+0)=75;
б)
“-” “+”
=1·(-1)7+(-2) 4·(-5)+0·3·0-(0·(-1)·(-5)+1·4·0+(-2)·3·7)=-7+40+42=75.
Приведённые выше правила вычисления определителей второго и третьего порядка применимы только к таким определителям. Для вычисления определителей четвёртого и более высоких порядков нужны новые понятия.
Определение 3. Минором Mij элемента aij матрицы n-го порядка
называется определитель (n – 1)-го порядка, получающийся из данного определителя матрицы А вычёркиванием i-й строки и j-го столбца (строки и столбца, в которых стоит элемент aij).
19
Определение 4. Алгебраическим дополнением Аij элемента
aijопределителя n-го порядка называется число, равное( 1)i j Mij, т.е.
Aij 1 i jMij, |
(1.3) |
где i – номер строки, j – номер столбца а пересечении которых стоит элемент aij
Из формулы (1.3) следует, что алгебраическое дополнение Аijотличается от отвечающего ему минора Mijтолько знаком, т.е. Аij Mij, если сумма индексов (i + j) является чётным числом, и Аij Mij, если (i + j) – нечётное число.
Пример 1.2. Вычислить миноры M22,M34 и отвечающие им алгебраические дополнения А22,A34, если
2 |
1 |
0 |
1 |
|
||
|
1 |
3 |
2 |
0 |
|
|
|
|
|||||
A = |
1 |
1 |
3 |
1 |
. |
|
|
|
|||||
|
|
|
|
|||
|
0 |
1 |
0 |
2 |
|
|
|
|
|||||
Решение.
|
2 |
|
1 |
0 |
1 |
|
|
2 |
0 |
1 |
|
|
||
|
|
|
|
|
||||||||||
|
|
|
||||||||||||
M22 |
1 |
|
3 |
2 |
0 |
|
|
1 |
3 |
1 |
|
( 2) 3 2 12; |
||
1 |
|
1 |
3 |
1 |
|
|||||||||
|
0 |
|
1 |
0 |
2 |
|
|
0 |
0 |
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A22 ( 1)2 2 |
( 12) 12; |
|
|
|
|
|
|
|||||||
|
2 |
1 |
0 |
1 |
|
|
2 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|||||||||
M34 |
1 |
3 |
2 |
0 |
|
|
1 |
3 |
2 |
|
( 2) 2 1 4; |
|||
1 |
1 |
3 |
1 |
|
|
|||||||||
|
0 |
1 |
0 |
2 |
|
|
0 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
A34 ( 1)3 2 4 4.
Ответ: M22 12, А22 12; M34 4, А34 4.
Опрделение 5. Определитель n-го порядка равен сумме произведений элементов первой строки определителя на их алгебраические дополнения, т.е.
a11 a12 a21 a22
... ...
an1 an2
... |
a1n |
|
a11A11 a12A12 |
... a1nA1n |
a1jA1j . (1.4) |
|
|||||
... |
a2n |
|
|||
|
|
|
|
|
n |
... |
... |
|
|
|
j 1 |
... |
ann |
|
|
|
|
20
Вычисление определителя по формуле (1.4) называют разложением определителя n-го порядка по первой строке.
Можно показать, что разлагать определитель можно по его любой строке и по любомустолбцу:
|
a11 |
a12 |
... |
a1j |
... |
a1n |
|
|
|
|
|
|
|
|
|
|
|||||||
|
a21 |
a22 |
... |
a2j |
... |
a2n |
|
|
|
|
|
|
... |
... |
... |
... |
... |
... |
|
ai1Ai1 |
ai2Ai2 |
... ainAin |
(1.5) |
|
ai1 |
ai2 |
... |
aij |
... |
ain |
|
|
|
|
|
|
... |
... ... ... ... ... |
|
|
|
|
|
||||
|
an1 |
an2 |
... |
anj |
... |
ann |
|
|
|
|
|
|
|
|
|
=a1jA1j a2jA2j ... anjAnj. |
|
(1.6) |
|||||
Формула (1.5) даёт разложение определителя по некоторой i-й строке, где i – любое из чисел 1, 2, …, n. Формула (1.6) даёт разложение по j-му столбцу,
где также j 1,2,...,n .
Пример 1.3. Вычислить определитель матрицы А, приведённой в примере 1.2, разложив его по четвёртой строке.
Решение.
|
2 |
1 |
0 |
1 |
|
|
|
1 0 |
1 |
|
2 |
0 |
1 |
|
2 1 |
1 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
||||||||||||||
|
1 3 |
2 |
0 |
|
|
|
|
|
|
|||||||||
|
|
|
0 ( 1) |
3 2 |
0 |
1 |
1 |
2 |
0 |
0 ( 1) |
1 3 |
0 |
|
|||||
|
1 |
1 |
3 |
1 |
|
1 3 |
1 |
|
1 |
3 |
1 |
|
1 1 |
1 |
|
|||
|
0 |
1 |
0 |
2 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2 |
|
2 |
1 |
0 |
|
|
|
А41 |
|
А42 |
|
|
А43 |
|
|
|||
|
|
|
|
|
|
|
|
|||||||||||
|
1 |
3 |
2 |
|
|
0 (4 3 2) 2 ( 18 2 4 3) 29. |
|
|
|
|||||||||
|
|
|
1 |
1 |
3 |
|
|
|
А42 |
|
|
|
А44 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
А44
Ответ: А = 29.
Наличие двух нулей в четвёртой строке, по которой производится разложение, избавило нас от необходимости вычислять два определителя третьего порядка.
Нельзя ли преобразовывать определитель так, чтобы в некоторой строке (столбце) получались нули, а значение определителя при этом не изменялось? Оказывается, что такие преобразования возможны. Основываются эти преобразования на свойствах определителей, основным среди которых является следующее свойство: если к элементам какой-либо строки (столбца)
определителя прибавить соответствующие элементы другой строки
21
(столбца), умноженные на произвольное число , то величина определителя не изменится, т.е., если
|
а11 |
a12 |
... |
a1n |
|
|
|
а11 |
a12 |
... |
a1n |
|
|
|
|
|
|||||||||
|
a21 |
a22 |
... |
a2n |
|
|
|
a21 |
a22 |
... |
a2n |
|
A= |
... |
... ... ... |
, |
А1= |
|
... |
... |
... |
... |
, |
||
ai1 |
ai2 |
... |
ain |
|
ai1 а11 |
ai2 а12 |
... |
ain а1n |
||||
|
... |
... ... ... |
|
|
|
... |
... |
... |
... |
|
||
|
an1 |
an2 |
... |
ann |
|
|
|
an1 |
an2 |
... |
ann |
|
то A1 A.
Пример 1.4. Вычислить определитель матрицы А, приведённой в примере 1.2, получив нули в некоторой строке или в некоторой строке или в некотором столбце.
Решение. В четвёртой строке уже есть два нуля, поэтому удобно получить ещё один нуль и потом вычислить определитель, разложив его по четвёртой строке. Для этого прибавим к каждомуэлементу 4-го столбца соответствующие элементы 2-го столбца, умноженные на (-2), т.е. к 4-му столбцу прибавим 2-й, умноженный на (-2):
2 |
1 0 |
1 |
|
2 1 0 |
1 ( 2) 1 |
|
|
|
|
2 |
1 0 |
1 |
|
||
|
|
|
|
|
|||||||||||
1 |
3 2 |
0 |
|
1 |
3 2 |
0 ( 2) 3 |
|
|
|
1 |
3 2 |
6 |
|
||
1 |
1 3 |
1 |
|
1 |
1 3 |
1 ( 2) 1 |
|
|
|
|
1 |
1 3 |
3 |
|
|
0 |
1 0 |
2 |
|
0 |
1 0 |
2 ( 2) 1 |
|
|
|
|
0 |
1 0 0 |
|
||
|
|
|
|
|
|
|
|
|
|
|
2 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
0 А41 1 А42 0 А43 0 А44 1 |
1 |
2 |
6 |
. |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
3 |
3 |
|
|
Для вычисления полученного определителя третьего порядка вновь получим нуль, например, в 1-й строке:
|
|
|
|
2 |
0 |
1 |
|
2 ( 2)( 1) |
0 |
|
1 |
|
|
|
0 |
0 |
1 |
|
||
|
|
|
|
|
|
|
|
|||||||||||||
|
А |
|
|
1 |
2 |
6 |
|
1 ( 2)( 6) |
2 |
|
6 |
|
|
|
13 |
2 |
6 |
|
||
|
|
|||||||||||||||||||
|
|
|
|
1 |
3 |
3 |
|
1 ( 2)( 3) |
3 |
|
3 |
|
|
|
5 |
3 |
3 |
|
||
0 А11 0 А12 ( 1) А13 1 |
|
13 |
2 |
|
(13 3 2 5) 29. |
|||||||||||||||
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
5 |
3 |
|
|
|
|
|
|
|
|
|
Ответ: А = 29.
22
II. Решение СЛАУ по правилу Крамера
Рассмотрим систему трёх линейных уравнений с тремя неизвестными, записанную в общем виде:
a11x1 a12x2a21x1 a22x2a31x1 a32x2
Утверждение. Если определитель
a13x3 |
|
b1, |
|
|
|
a23x3 |
|
b2, |
(1.7) |
|
a33x3 |
|
b3. |
|
|
|
a11 |
a12 |
a13 |
|
основной |
|
|
|||||
|
a21 |
a22 |
a23 |
|
||
|
|
a31 |
a32 |
a33 |
|
|
матрицы СЛАУ (1.7) не равен нулю, то система уравнений при любой правой части имеет единственное решение, которое находится по формулам:
|
|
|
|
|
|
x |
1 |
|
1 , |
x |
2 |
|
2 , |
|
x |
3 |
|
3 |
, |
|
|
|
|
(1.8) |
||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
|
b1 |
a12 |
a13 |
|
, |
2 |
|
|
a11 |
|
b1 |
a13 |
|
, |
|
3 |
|
a11 |
a12 |
b1 |
|
. |
|
||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
b2 |
a22 |
a23 |
|
|
a21 |
|
b2 |
a23 |
|
|
|
a21 |
a22 |
b2 |
|
(1.9) |
|||||||||||
|
|
b3 |
a32 |
a33 |
|
|
|
|
|
|
a31 |
|
b3 |
a33 |
|
|
|
|
|
|
|
a31 |
a32 |
b3 |
|
|
|
|
Сформулированное утверждение называется правилом Крамера. Пример 1.5. Решить систему методом Крамера:
5x1 x2 7x3 2,3x1 2x2 2x3 5,
x1 x2 x3 2.
Решение. Вычислим определитель основной матрицы А:
|
|
5 |
1 |
7 |
|
|
|
5 |
6 |
6 |
|
|
|
|
|
|
|||||||||
|
|
3 |
2 2 |
|
|
|
3 |
1 |
0 |
|
6 0. |
|
|
|
1 |
1 |
1 |
|
|
|
1 |
0 |
0 |
|
|
Для вычисления определителя были получены нули в третьей строке. Для этого из второго столбца вычли первый; к третьему столбцу прибавили первый столбец. Следовательно, система имеет единственное решение. Для нахождения этого решения вычислим определители 1, 2, 3 по формулам
(1.9):
23
|
2 |
1 |
7 |
|
|
|
2 |
1 |
6 |
|
|
|
|
|
|
||||||||
1 |
5 |
2 2 |
|
|
|
5 |
2 0 |
|
6 1 6, |
||
|
2 |
1 |
1 |
|
|
|
2 |
1 |
0 |
|
|
|
|
5 |
2 |
7 |
|
|
|
|
5 |
7 |
2 |
|
|
|
|
|
|
||||||||||
2 |
|
3 |
5 |
2 |
|
0, |
3 |
|
3 |
2 |
5 |
|
6. |
|
|
1 |
2 |
1 |
|
|
|
|
1 |
1 |
2 |
|
|
В соответствии с формулами (1.8) получаем решение СЛАУ:
x |
1 |
|
1 |
|
6 |
1, |
x |
2 |
|
2 |
|
0 |
0, |
x |
3 |
= |
3 |
= -1. |
|
6 |
6 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Проверка. Подставляем найденные значения x1,x2,x3 последовательно
в левые части уравнений:
(1-го уравнения)=5 1 0 7 ( 1) 2, (2-го уравнения)=3 1 2 0 2 ( 1) 5, (3-го уравнения)=1 0 ( 1) 2.
Поскольку полученные числовые значения в левой части каждого уравнения СЛАУ совпадают со значениями правых частей, то найдено искомое решение СЛАУ
|
1 |
X |
0 . |
|
|
|
1 |
Ответ: x1 1, x2 0, x3 1.
