
For Exam / Прямая и плоскость в пространстве 2
.pdf
Уравнения прямой и плоскости в пространстве
Основные теоретические сведения
Плоскость в пространстве в декартовой прямоугольной системе координат 0xyz может быть задана уравнением одного из следующих видов:
|
|
|
|
|
|
|
Ax By Cz D 0 - |
(4.1) |
|||||||||||||||
общее уравнение плоскости; |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
A x x0 B y y0 C z z0 0 - |
(4.2) |
||||||||||||||||||
уравнение плоскости, |
проходящей через точку M x0;y0;z0 ,перпендикулярно |
||||||||||||||||||||||
к вектору нормали |
|
A;B;C ; |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
N |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
||||
или в скалярной форме |
M0M |
a |
b |
|
|||||||||||||||||||
|
|
x x0 |
y y0 |
z z0 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
x1 |
|
|
y1 |
z1 |
|
0 - |
(4.3) |
||||||||
|
|
|
|
|
|
|
x2 |
|
|
y2 |
z2 |
|
|
|
|||||||||
уравнение плоскости, |
проходящей через точку M x0;y0;z0 |
и параллельной |
|||||||||||||||||||||
векторам |
|
x1;y1;z1 , |
|
x2;y2;z2 ; |
|
|
|
|
|||||||||||||||
a |
b |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
y |
|
z |
1 - |
|
|
|
(4.4) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
a b |
|
|
c |
|
|
|
|
||||||||
уравнение плоскости в отрезках (a,b,c - отрезки, отсекаемые на координатных осях Ox,Oy,Oz соответственно);
|
x x1 |
y y1 |
z z1 |
|
|
|
x2 x1 |
y2 y1 |
z2 z1 |
0 - |
(4.5) |
|
x3 x1 |
y3 y1 |
z3 z1 |
|
|
уравнение плоскости, проходящей |
через три точки |
M1 x1;y1;z1 , |
|||
M2 x2;y2;z2 , M3 x3;y3;z3 , не лежащие на одной прямой. Прямая L в пространстве может быть задана
а) общими уравнениями – как пересечение двух непараллельных плоскостей
A |
x B |
y C z D 0, |
(4.6) |
||||||
L: 1 |
1 |
|
1 |
1 |
|
|
|
||
A2x B2y C2z D2 0; |
|
||||||||
б) каноническими уравнениями |
|
|
|
|
|
|
|||
|
L: |
x x0 |
|
y y0 |
|
z z0 |
, |
(4.7) |
|
|
|
m |
|
||||||
|
|
|
l |
|
|
n |
|
||
где M x0;y0;z0 - точка, через которую проходит прямая; q l;m;n - направляющий вектор прямой;
в) параметрическими уравнениями
x x0 |
tl, |
|
|
tm, |
(4.8) |
L: y y0 |
||
|
tn. |
|
z z0 |
|
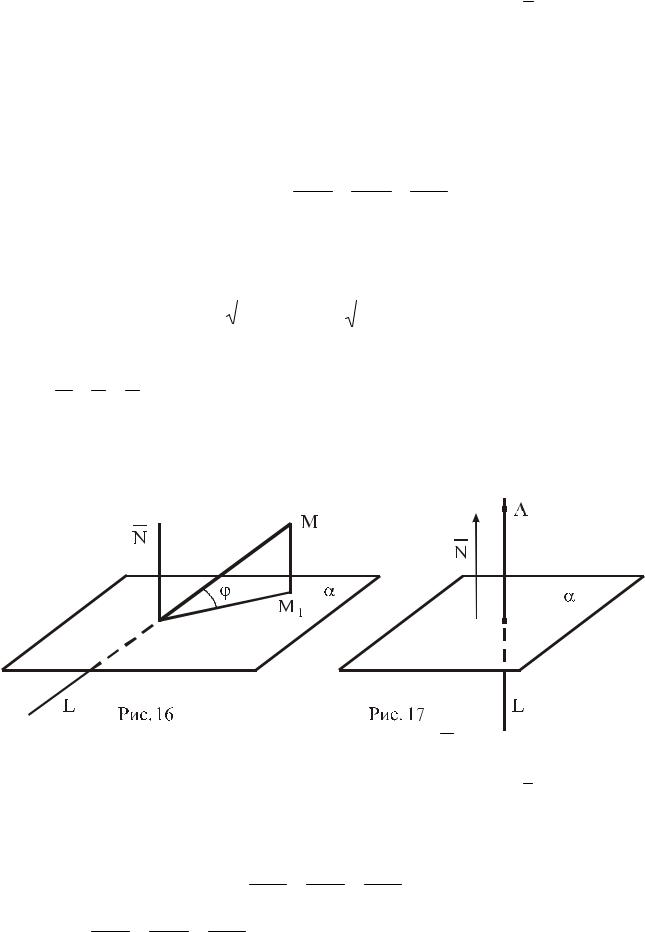
Углом между прямой ( L ) : x a y b z c и плоскостью m n p
:Ax By Cz D 0 (см. рис. 16) называется острый угол между прямой и ее проекцией на плоскость.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
sin |
|
N,a |
|
Am Bn Cp |
|
, |
(4.9) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
N |
a |
|
|
|
A2 B2 C2 |
|
m2 n2 p2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
Am Bn Cp 0-условие параллельности прямой и плоскости.
A B C - условие перпендикулярности прямой и плоскости. m n p
Решение типовых задач
Пример 4.1. Из точки А(3;-2;4) опустить перпендикуляр на плоскость
5x 3y 7z 1 0 ( ).
Решение. Нормальный вектор плоскости |
N (5;3; 7) можно |
считать направляющим вектором прямой L |
(см. рис. 17). Прямая L |
проходит через точку A 3; 2;4 и имеет направляющий вектор q 5;3; 7 . В соответствии с формулой (4.7) получим уравнения искомого перпендикуляра:
x 3 y 2 z 4.
5 |
3 |
7 |
Ответ: L: x 3 y 2 z 4 .
5 |
3 |
7 |

Пример 4.2. |
Найти точку пересечения |
прямой |
|
x 1 |
|
y 1 |
|
z |
и |
|||||||||||||||||||||||||
1 |
|
|
||||||||||||||||||||||||||||||||
плоскости 2x 3y z 1 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 6 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Решение. Запишем уравнения прямой в параметрической форме и |
||||||||||||||||||||||||||||||||||
решим систему уравнений: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
x t 1, y 2t 1, |
z 6t, |
|
|
|
(4.10) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z 1 0, |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
2x 3y |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
откуда 2(t 1) 3( 2t 1) 6t 1 0, t 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Подставив t 1 в (4.10), |
получим x 1 1 2, |
y -2 1-1 -3, z 6 1 6. |
||||||||||||||||||||||||||||||||
Таким образом, Р(2;-3;6) является искомой точкой пересечения прямой и |
||||||||||||||||||||||||||||||||||
плоскости. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Ответ: P 2; 3;6 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Пример 4.3. |
Составить уравнение плоскости, проходящей через |
|||||||||||||||||||||||||||||||||
точку M(1;2; 3), параллельно прямым |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
x 1 |
|
y 1 |
|
z 7 |
, |
|
x 5 |
|
y 2 |
|
z 3 |
. |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
|
|
|
|
2 |
1 |
|
|
|
|
|
|||||||||
Решение. |
Искомая |
плоскость параллельна |
данным прямым, |
|||||||||||||||||||||||||||||||
следовательно, ее нормальный вектор |
N |
перпендикулярен направляющим |
||||||||||||||||||||||||||||||||
векторам |
|
1 2; 3;3 и |
|
|
2 3; 2; 1 |
прямых |
L1 и |
L2 . Поэтому можно |
||||||||||||||||||||||||||
q |
q |
|||||||||||||||||||||||||||||||||
принять |
|
|
|
|
|
2 , т.е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
N |
q |
1,q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
i j k
N 2 |
3 |
3 9i 11j 5k. |
3 2 1
Имеем задачу: составить уравнение плоскости, проходящей через точку M(1;2; 3), перпендикулярно к вектору N 9;11;5 . В соответствии с (4.2) уравнение плоскости будет иметь вид
9(x 1) 11(y 2) 5(z 3) 0 или 9x 11y 5z -16 0.
Ответ: : |
9x 11y 5z 16 0. |
|
|
|
|
||
Пример 4.4 Составить уравнение плоскости , проходящей через |
|||||||
прямую |
|
x 1 |
|
y 2 |
|
z 2 |
|
|
|
|
|
, |
|||
|
2 |
3 |
|
||||
|
|
2 |
|
||||
перпендикулярно к плоскости 3x 2y z 5 0 |
( 1). |

Решение. |
|
Из |
|||
условия задачи |
и |
рис.18 |
|||
следует, |
что |
|
вектор |
||
нормали |
N |
искомой |
|||
плоскости |
должен быть |
||||
перпендикулярен |
|
к |
|||
вектору |
|
|
3;2; 1 |
||
|
N1 |
||||
нормали |
плоскости |
1 и |
|||
направляющему |
вектору |
||||
q 2; 3;2 прямой L.
Следовательно, можно положить |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
k |
|
|
|
|
|
|
|
||
|
|
|
|
|
2 |
3 |
2 |
|
|
|
|
|
|
||||||
|
N |
a, |
N1 |
i 8j |
13k. |
||||||||||||||
|
3 |
2 |
1 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Точка M(1; 2;2) . Применяем формулу (4.2):
1(x 1) 8(y 2) 13(z 2) 0,
x 8y 13z 9 0,
x 8y 13z 9 0.
Полученное уравнение является уравнением искомой плоскости .
Ответ: :x 8y 13z 9 0.
