
For Exam / Тройные интегралы
.pdf1) Определение тройного интеграла
Основные понятия и теоремы для тройных интегралов аналогичны соответствующим понятиям и теоремам для двойных интегралов. Пусть T – кубируемая область (открытая и замкнутая) в трехмерном евклидовом пространстве и пусть в области T определена ограниченная функция u=f(M)=f(x,y,). Разобьем область T на n кубируемых частей Ti (i=1,2,…,n) так, чтобы любые две
части не имели общих внутренних точек, в каждой части возьмем произвольную точку Mi ( i , i , i ) и составим интегральную сумму,
n
I (Ti , Mi ) f ( i , i , i ) Vi
i 1
где Vi - объем Ti , d max di .
1 i n
Определение. Число I называется пределом интегральных сумм I (Ti , M ) при d → 0, если ϵ>0 δ>0
такое, что для любого разбиения области T, у которого d<δ , и для любого выбора промежуточных точек Mi , выполняется неравенство
I ( Ti , Mi )−I <ϵ.
Если существует lim I (Ti , Mi ) I , то он называется
d 0
тройным интегралом от функции f(x,y,z) по области T и
обозначается f (x, y, z)dxdydz |
или f (M )dV , а |
T |
T |
функция f(x,y,z) называется интегрируемой в области T.
Теорема 5. Функция, непрерывная в замкнутой кубируемой области, интерпретируема в этой области.
Теорема 6. Функция, ограниченная в кубируемой области и непрерывная всюду, кроме некоторого множества точек объѐма нуль, интегрируема в этой области.

Тройные интегралы обладают такими же свойствами, как определѐнные и двойные интегралы (линейность, аддитивность, формулы среднего значения и т. д.)
2) Вычисление тройных интегралов с помощью
повторного интегрирования. |
|
|
Пусть функция f(x,y,z) определена в |
области |
|
T {(x, y, z) : |
(x, y) G, z1(x, y) z z2 (x, y)} , где z1 (x, y) и |
|
|
z2 (x, y) - непрерывные |
|
|
функции |
в |
|
квадрируемой |
области |
|
G (рисунок 8). |
|
Рисунок 8
Теорема 7. Пусть:
1 ) существует тройной интеграл
f (x, y, z)dxdydz;
T
2) (x, y) G существует определенный интеграл
z2 ( x, y )
I (x, y) f (x, y, z)dz.
z1 ( x, y )
Тогда существует двойной интеграл
|
|
z2 |
( x, y) |
I (x, y)dxdy dxdy |
|
f (x, y, z)dz |
|
G |
G |
z1 ( x, y ) |
|
(он называется повторным) и справедливо равенство
|
|
z2 ( x, y ) |
|
|
f (x, y)dxdydz dxdy |
|
f (x, y, z)dz, |
(1) |
|
T |
G |
z1 ( x, y ) |
|
|
т.е. тройной интеграл равен повторному. |
|
|||
Если область G является y-трапециевидной (см. |
||||
рисунок 8), т.е. G {(x, y) : a x b, |
y1 (x) y y2 (x)}, то |
|||
двойной интеграл |
I (x, y)dxdy в |
свою очередь |
можно |
|
G
свести к повторному:
|
b |
y2 ( x) |
b |
y2 ( x) |
z2 ( x) |
I (x, y)dxdy dx |
|
I (x, y)dy dx |
|
dy f (x, y, z)dz. |
|
G |
a |
y1 ( x) |
a |
y1 ( x) |
z1 ( x) |
Таким образом, вычисление тройного интеграла сводится в этом случае к последовательному вычислению трех определенных (однократных) интегралов:
b
f (x, y, z)dxdydz dx
T a
y2 ( x) |
z2 |
( x, y ) |
dy |
|
f (x, y, z)dz. |
y1 ( x) |
z1 ( x, y ) |
|
В формуле (1) повторный интеграл представляет собой двойной интеграл, а внутренний интеграл в повторном является определѐнным интегралом. Возможно и иное сведение тройного интеграла к повторному, когда повторный интеграл представляет собой определѐнный интеграл, а внутренний интеграл в повторном
является двойным интегралом.
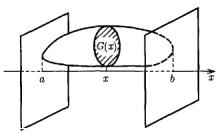
Пусть функция f(x,y,z) определена и ограничена в области T, которая заключена между плоскостями x=a и x=b, причѐм каждое сечение области T плоскостью x=const
(a ≤ x ≤ b) представляет собой квадрируемую фигуру G(x) (рисунок 9).
Теорема 8. Пусть:
1) существует тройной интеграл f (x, y, z)dxdydz;
T
2) x [a, b] существует двойной интеграл
I (x) f (x, y, z)dydz.
G( x)
Тогда существует определѐнный интеграл
|
b |
b |
|
|
|
I (x)dx |
dx |
f (x, y, z)dydz |
|
|
a |
a G( x) |
|
|
(он называется повторным) и справедливо равенство |
|
|||
|
b |
|
|
|
f (x, y, z)dxdydz dx |
f (x, y, z)dydz. |
(2) |
||
T |
a |
G( x) |
|
|
3) Замена переменных в тройном интеграле.
Аналогично случаю двойного интеграла замена переменных в тройном интеграле f (x, y, z)dxdydz
T
состоит в переходе от переменных x, y, z к новым переменным u, по формулам
x u, v, w , y u, v, w , z u, v, w , u, v, w . (3)
При этом каждая точка (x,y,z) области T соответствует по формулам (3) некоторой точке u, v, w области , а каждая
точка u, v, w области переходит в некоторую точку
(x,y,z) области |
T. Иными словами, функции (3) |
||
осуществляют |
|
отображение области |
пространства |
u, v, w на |
область T пространства |
(x,y,z). Пусть |
|
отображение (3) |
удовлетворяет таким же условиям, что и в |
||
предыдущем параграфе. |
|
||

I Отображение (3) взаимно однозначно
II Функции u, v, w , u, v, w и u, v, w имеют в
области непрерывные частные производные первого порядка
III Якобиан отображения D(x, y, z) отличен от нуля
D(u, v, w)
в области .
Теорема 9. Пусть и T - замкнутые кубируемые области, функция f(x,y,z) ограничена в области T и непрерывная всюду, кроме, быть может, некоторого множества точек объема нуль, а отображение (3) удовлетворяет условиям I - III
Тогда справедливо равенство (формула замены переменных в тройном интеграле)
f (x, y, z)dxdydz
T
D(x, y, z)
f ( u,v, w u,v, w , u,v, w ) D u,v, w dudvdw
T
Замечание. Формула замены переменных остаѐтся в силе, если условия I и III нарушаются на множестве точек объема нуль.
4) Криволинейные координаты.
Формулы (3) можно рассматривать как формулы перехода к новым, криволинейными координатам u, v, w в области T.
Поверхности u=const, v=const, и w=const представляют собой координатные поверхности (вообще говоря, криволинейные) в пространстве (x,y,z). Кривые, на которых две криволинейные координаты имеют постоянные значения и изменяется только одна из координат, представляют собой координатные линии.
Рассмотрим два примера наиболее употребительных криволинейных координат.

Цилиндрические координаты.
Пусть M(x,y,z) - произвольная точка в пространстве (x,y,z), M’- проекция точки M на
|
плоскость (x,y) (рисунок 10). |
||||
|
Точка M однозначно задаѐтся |
||||
|
тройкой |
чисел ( , , z) , где |
|||
|
( , ) - |
полярные |
координаты |
||
|
точки M’ на плоскости (x,y), z - |
||||
|
аппликата точки M. Трока чисел |
||||
|
( , , z) |
|
|
называется |
|
|
цилиндрическими |
кордонами |
|||
|
точки |
M. |
Переход |
от |
|
|
прямоугольных координат (x,y,z) |
||||
Рисунок 10 |
к цилиндрическим ( , , z) |
||||
задается формулами |
|
|
|||
|
|
|
|||
x cos , |
y sin , |
z z |
|
|
|
(0 , |
0 2 , |
z ) |
(4) |
||
(иногда в качестве промежутка изменения берется промежуток ).
Якобиан отображения (4) есть
D(x, y, z)
D u,
Координатная поверхность =const представляет собой
цилиндрическую поверхность – отсюда и название «цилиндрические координаты».

Сферические координаты.
Пусть M(x,y,z) – произвольная точка в пространстве (x,y,z), M’ – проекция точки M на плоскость
(x,y) (рисунок 11). Точка M однозначно задается тройкой чисел (r, , ) , где r – расстояние до точки
M от точки O (начала координат), - |
|
|
||||
угол между лучами OM и Oz , |
- |
|
|
|||
полярный угол |
|
точки |
M’ |
на |
|
|
плоскости (x,y). Тройка чисел |
|
|
||||
называется (r, , ) сферическими |
|
|
||||
координатами точки M. Переход от |
|
|
||||
прямоугольных координат (x,y,z) к |
|
|
||||
сферическим |
(r, , ) |
задаѐтся |
Рисунок 11 |
|
||
формулами |
|
|
|
|
|
|
|
|
|
|
|
|
|
x r sin cos , y r sin sin , |
z r cos |
|
||||
(0 r , |
0 , |
0 2 ) |
(5) |
|||
(Иногда в качестве угла |
берется угол между лучами OM |
|||||
и OM’ со знаком плюс если z>0, и со знаком минус, если z<0. В этом случае / 2 / 2 , а в формулах (5) нужно заменить sin на cos , а cos на sin ).
Якобиан отображения (5) |
есть |
D(x, y, z) |
r2 sin (в |
||||
D(r, , ) |
|||||||
|
|
|
|
|
|||
случае второго способа выбора |
угла |
якобиан равен |
|||||
r2 cos ). |
Координатная |
поверхность |
r=const>0 |
||||
представляет |
собой сферу |
– |
отсюда |
и |
название |
||
«сферические координаты».
Иногда используются так называемые обобщенные сферические координаты. Они связаны с прямоугольными координатами
x x |
arn sin cos |
, |
y y |
brn sin sin , |
0 |
|
|
0 |
|
|
z z |
crn cos |
||
|
0 |
|
|
|
(0 r , |
0 , |
|
0 2 ) , |
где x0 , y0 , z0 , a, |
b, c, n, , |
|
– некоторые числа, |
выбираемые в каждом конкретном случае из соображений удобства.
Якобиан перехода к обобщенным сферическим координатам имеет вид
D(x, y, z) |
3n 1 |
|
2 1 |
1 |
|
1 |
|
1 |
|
(6) |
|
|
|
|
|
|
|
||||||
D(r, , ) abcn r |
|
sin |
|
cos |
sin |
|
cos |
|
|
|
|
5) Вычисление объемов с помощью тройных интегралов.
Объем V кубируемой области T (кубируемого тела) в пространстве (x,y,z) выражается формулой
V dxdydz |
(7) |
|
T |
|
|
Если T {(x, y, z) : (x, y) G, |
0 z f (x, y)} ,где |
G - |
квадрируемая область на плоскости (x,y) , а f(x,y) - непрерывная в области G функция, то, сводя тройной интеграл к повторному, придем к формуле (9) из предыдущего параграфа, выражающей объѐм тела T через двойной интеграл:
V dxdy |
f ( x, y ) |
dz z |
0 |
dxdy f (x, y)dxdy. |
(8) |
|
|||||
|
|
|
f ( x, y ) |
|
|
G |
0 |
G |
|
G |
|
Если область T заключена между плоскостями x=a и x=b и каждое сечение области T плоскостью x=const представляет собой квадрируемую фигуру G(x) с площадью S(x), то, сводя тройной интеграл (7) к
повторному по формуле (2) и учитывая, что, dydz S(x)
G ( x)
придем к известному выражению объема теле с помощью определенного интеграла

b |
|
b |
V dx |
dydz S(x)dx |
|
a |
G ( x) |
a |
Переходя в равенстве (7) к новым переменным u, v, w по формулам (3), получим выражение объема области T в криволинейных координатах:
D(x, y, z)
V D u, v, w dudvdw
T
Величину dV = dx dy dz ,представляющую собой объем прямоугольного параллелепипеда с ребрами dx, dy, dz,
естественно называть элементом объема в прямоугольных
координатах , а величину |
dV |
D(x, y, z) |
|
dudvdw |
- |
|
D u, v, w |
||||||
|
|
|
|
|
элементом объема в криволинейных координатах u, v, w.
Модуль якобиана |
D(x, y, z) |
|
представляет собой |
|
|
|
|||
D u, v, w |
||||
|
|
|
||
|
|
|
|
коэффициент растяжения объема в точке (u,v,w) при отображении области пространства u, v, w на область T
пространства (x,y,z).
6) Физические приложения тройных интегралов.
Пусть T – материальное тело (кубируемая область в
пространстве Oxyz) с плотностью |
(x, y, z) . |
Тогда |
|
справедливы следующие формулы: |
|
|
|
а) m (x, y, z)dxdydz - масса тела; |
|
||
T |
|
|
|
б) M yz x (x, y, z)dxdydz , |
M zx y (x, y, z)dxdydz , |
||
T |
|
T |
|
M xy z (x, y, z)dxdydz - статические |
моменты |
тела |
|
T |
|
|
|
относительно координатных плоскостей Oyz , Ozx , Oxy ;

в) |
x |
|
M yz |
, y |
M |
zx |
, z |
|
|
M xy |
- координаты центра |
|
|
|
0 |
|
|||||||
|
0 |
|
m |
0 |
m |
|
m |
|
|||
|
|
|
|
|
|
|
|||||
тяжести тела; |
|
|
|
|
|
|
|
|
|||
г) |
I yz |
x2 (x, y, z)dxdydz , |
Izx y2 (x, y, z)dxdydz , |
||||||||
|
|
|
T |
|
|
|
|
|
|
|
T |
Ixy z2 (x, y, z)dxdydz - |
моменты инерции относительно |
T |
|
координатных плоскостей Oyz , Ozx , Oxy ; |
|
д) Ix Izx Ixy , I y |
Ixy I yz , Iz I yz Izx - моменты |
инерции тела относительно координатных плоскостей Oyz ,
Ozx , Oxy ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е) |
IO |
I yz Izx Ixy |
(x2 y2 z2 ) (x, y, z)dxdydz - |
||||||||||||||||||
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
момент инерции тела относительно начала координат; |
|
||||||||||||||||||||
ж) U (x0 , y0 , z0 ) |
(x, y, z) |
1 |
dxdydz |
|
- ньютоновский |
||||||||||||||||
|
|||||||||||||||||||||
|
|
|
|
|
|
T |
|
|
r |
|
|
|
|
|
|
|
|
|
|
||
потенциал поля тяготения тела T в точке (x0 , y0 , z0 ) ; |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
здесь |
r |
|
(x x )2 ( y y )2 |
(z z |
)2 |
|
|
|
|
|
- расстояние |
||||||||||
|
|
|
|
|
0 |
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
между точками M(x,y,,z) |
и |
|
M0 (x0 , y0 , z0 ) , |
- |
|||||||||||||||||
гравитационная постоянная; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
з) |
F {Fx , Fy , Fz } - |
сила притяжения материальной |
|||||||||||||||||||
точки M0 (x0 , y0 , z0 ) |
массы m0 телом T, где |
|
|
|
|
|
|||||||||||||||
|
|
m0 |
U |
m0 |
(x, y, z) |
x x |
|
||||||||||||||
|
Fx |
|
|
|
|
0 |
|
|
dxdydz, |
|
|||||||||||
|
x0 |
|
r |
3 |
|
|
|
||||||||||||||
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
m0 |
U |
m0 |
(x, y, z) |
y y |
|
||||||||||||||
|
Fy |
|
|
|
|
|
0 |
dxdydz, |
|
||||||||||||
|
t0 |
|
r |
3 |
|
|
|
||||||||||||||
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Fz |
m0 |
U |
m0 |
(x, y, z) |
|
z z |
0 |
dxdydz. |
|
|||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
z0 |
|
|
r |
3 |
|
|
||||||||||||||
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
