For Exam / Прямая и плоскость в пространстве 1

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Рязанский государственный радиотехнический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Здесь a,b,c

- величины отрезков

.pdf

Скачиваний:

Добавлен:

15.04.2015

Размер:

324.83 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

3.3. Плоскость

3.3.1.Уравнение плоскости,

проходящей через три заданные точки

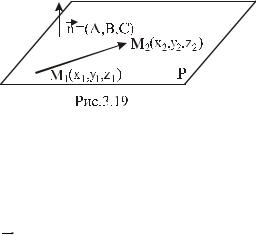
Задача 1. Составить уравнение плоскости P, проходящей через три заданные точки M1 x1;y1;z1 ; M2 x2;y2;z2 ; M3 x3;y3;z3 , не лежащие на одной прямой.

Решение. Возьмем

произвольную точку

M x,y,z

в пространстве с заданной

прямоугольной системой координат Охуz и образуем векторы

(рис. 3.18):

M1M x x1;y y1;z z1 ;

M1M2 x2 x1;y2 y1;z2 z1 ;

M1M3 x3 x1;y3 y1;z3 z1 .

Точка M будет принадлежать плоскости P тогда и только тогда,

когда будут компланарны векторы M1M, M1M2, M1M3 . С

учетом свойств смешанного произведения это эквивалентно следующему равенству:

M1M M1M2 M1M3 0

(3.24)

или, переходя к координатной форме записи смешанного произведения,

x x1	y y1	z z1
x2 x1	y2 y1	z2 z1	0.	(3.25)
x3 x1	y3 y1	z3 z1

Это и есть искомое уравнение плоскости P, проходящей через

три заданные	точки M1 x1,y1,z1 ;	M2 x2,y2,z2 ;
M3 x3,y3,z3	в векторной (3.24) и координатной (3.25)

формах.

Справедлива следующая теорема. ■

Теорема 3.2. Уравнение произвольной плоскости в декартовой прямоугольной системе координат может быть записано в следующем виде:

Ax By Cz D 0 ,

(3.26)

и наоборот: всякое уравнение первой степени (3.26) определяет в пространстве (в заданной прямоугольной системе координат Oxyz) некоторую плоскость Р.

Определение 1. Уравнение (3.26) называется общим уравнением плоскости.

Заметим, что в уравнении (3.26) хотя бы один из коэффициентов A,B,C должен быть отличен от нуля.

Образуем из этих коэффициентов вектор n A,B,C .

Утверждение.

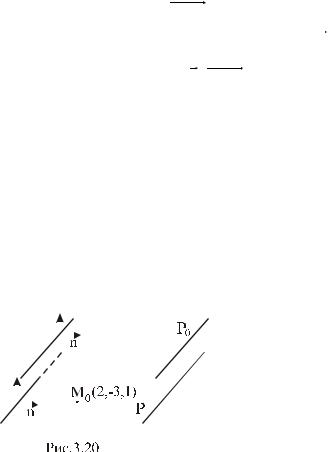
Вектор n A,B,C перпендикулярен к плоскости Р,

определяемой общим уравнением (3.26),

(рис. 3.19).

Доказательство утверждения проводится совершенно аналогично доказательству соответствующего утверждения для прямой на плоскости (раздел 3.2).

Определение 2. Всякий вектор n, перпендикулярный к плоскости P, называется вектором нормали этой плоскости,


т.е.	вектор	n A,B,C		и	любой	вектор
N A, B, C ,		R	и 0,		являются	векторами
нормали плоскости P:Ax By Cz D 0.

3.3.2. Уравнение плоскости, проходящей через заданную точку и перпендикулярной к заданному вектору

Задача 2. Составить уравнение плоскости P, проходящей

через заданную точку		M0 x0;y0;z0 и перпендикулярной		к
заданному вектору n A;B;C .
Решение.	Пусть	M x,y,z – произвольная	точка	в
искомой плоскости P,		не совпадающая с заданной точкой
M0 . Образуем	вектор M0M x x0; y y0 ; z z0 . Из
условия задачи имеем n P и значит n M0M.			Но тогда
		n, M0M 0	(3.27)
или в скалярной форме
A x x0 B y y0 C z z0 0.			(3.28)

Это и есть искомые уравнения плоскости Р, проходящей через

заданную точку M0 и перпендикулярной

заданному

вектору n. ■

Рассмотрим задачу на применение этих формул.

Пример 3.6. Составить уравнение плоскости Р, проходящей

через точку M0 2; 3;1 и параллельной

плоскости

P0 :4x y 5z 6 0 .

Решение.

По

условию

задачи

P|| P0.

Поэтому

вектор нормали

n 4; 1;5

плоскости

перпендикулярен

плоскости

P , т.е. его можно

взять в

качестве

вектора

нормали этой плоскости (рис. 3.20).

Тогда в соответствии с (3.28) получаем искомое уравнение

P:4 x 2 1 y 3 5 z 1 0,

или

P:4x y 5z 16 0. Ответ: P:4x y 5z 16 0.

Использование равенства нулю смешанного произведения трех компланарных векторов и равенства нулю скалярного произведения двух перпендикулярных векторов – два основных общих принципа построения уравнения плоскости. Все остальные являются производными от них.

3.3.3. Уравнение плоскости в отрезках

Частным случаем уравнения плоскости, проходящей через три заданные точки, является уравнение плоскости в

отрезках:

(взятых с соответствующим знаком),

отсекаемых	плоскостью	Р	на
координатных	осях	Ox;Oy;Oz

соответственно (рис. 3.21).

Пример 3.7. Составить уравнение плоскости Р, проходящей через точки

A 4;0;0 ; B 2; 3;6 ; C 0;0;3 .

Решение. Поскольку точка A лежит на оси Ox , а точка C

– на оси Oz , то удобно воспользоваться уравнением (3.29) при

a 4; c 3 и неопределенном пока параметре b :
	x	y	z	1.	(3.30)
	4		3
		b
Для определения параметра b			(величины отрезка,		отсекаемого

искомой плоскостью на оси Oy) подставим в уравнение (3.30)

координаты (2;-3;6) точки B. Они должны удовлетворять этому уравнению, так как по условию точка B P:

b 6.

Окончательно имеем

3x 2y 4z 12 0.

Ответ:

P: 3x 2y 4z 12 0.

3.3.4. Расстояние от точки до плоскости

Задача

Найти

расстояние

M0,P от

точки

M0 x0;y0;z0 до плоскости

Ax By Cz D 0.

Решение. Данная задача может

быть решена,

как и аналогичная ей

задача 5 поиска расстояния от

точки до прямой на плоскости,

двумя cпособами (п. 3.2.6).

Первый способ. 1. Проводим через

точку M0 x0;y0;z0 прямую L, L P (рис. 3.22),

x x0

y y0

z z0

(3.31)

2. Находим точку F пересечения прямой L с плоскостью

P , решая совместно уравнения (3.32)

x x

y y

z z

;

(3.32)

By Cz D 0.

3. Составляем вектор

M0F и находим его длину

M0F

Задача решена, так как M0,P

M0F

Второй способ. Расстояние M0,P находится по формуле

M0,P

Ax0 By0

Cz0 D

. ■

(3.33)

Найдем расстояние M0,P

A2 B2 C2

первым способом при следующих

данных: M0 2;1;7 ; P:

2x y 4z 2 0.

1. Так как nP 2; 1;4 , то

соответствии

с (3.31)

составляем уравнение прямой L P:

x 2

y 1

z 7

(3.34)

2. Для нахождения координат точки F перепишем предварительно уравнение (3.34) в параметрической форм:

x 2 y 1 z 7 t

x 2	2t,
y		(3.35)
y	1 t, .	(3.35)
z 7
z 7	4t.

Заменим в уравнении плоскости P переменные			x,y,z их
параметрическими аналогами (3.35):
2 2 2t 1 t 4 7 4t 2 0 21t 21			t 1.
Подставляя теперь t 1		в (3.35), получаем искомые
координаты точки F : xF 2		2 1;
yF	1 1 0;
zF	7 4 1	11, т.е. F 0;0;11 .

3. Составляем вектор

M0F 0 2 ; 0 1;11 7 2; 1; 4

и находим

M0,P M0F 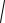22 1 2 42 21.

98
Читателю предлагается			самостоятельно	вычислить
M0,P в данной задаче			вторым способом,	т.е. по
формуле (3.33).
Ответ: M0,P		.
	21

3.3.5. Взаимное расположение плоскостей

Пусть P1 :A1x B1y C1z D1 0; P2 :A2x B2y C2z D2 0.

Как и прямые на плоскости, плоскости в пространстве могут пересекаться, быть параллельными и могут совпадать.

1. Плоскости параллельны. В этом случае					n1 \|\| n2
n1 A1;B1;C1 , n2	A2;B2;C2 и, как следствие,
	A1	B1	C1	.	(3.36)
	A2	B2
			C2

Условие (3.36) пропорциональности коэффициентов - необходимое и достаточное условие параллельности плоскостей P1 и P2 .

2. Плоскости совпадают:

A1	B1	C1	D1	.	(3.37)
A2	B2	C2
			D2

Замечание. Условие (3.37) означает, что все коэффициенты уравнения плоскости P можно умножить (разделить) на любое число, отличное от нуля. Получится новое уравнение, но определять оно будет ту же плоскость P.

3. Плоскости пересекаются.

В этом случае векторы n1 и n2 неколлинеарны и

;

(3.38)

Пример 3.8. Установить взаимное расположение плоскостей

а) 3x 2y z 3 0

6x 4y 3z 0;

б) x 3y 4z 2 0

4x 12y 16z 0;

в) x 2y z 3 0

2x 4y 2z 6 0.

Решение:

а) плоскости пересекаются, так как

;

б) плоскости параллельны, так как

;

в) плоскости совпадают, так как

Выделим еще условие перпендикулярности плоскостей.

Если P1 P2 , то и n1 n2 ,

но тогда n1,n2 0 или

A1A2 B1B2

C1C2 0.

(3.39)

Если в общем уравнении Ax By Cz D 0 плоскости

P часть коэффициентов A;B;C;D равна нулю, то:

A 0 - плоскость P параллельна оси Ox :

By Cz D 0;

B 0 - плоскость P параллельна оси Oy:

Ax Cz D 0;

C 0 - плоскость P параллельна оси Oz:

Ax By D 0;

A 0,

B 0

- плоскость

параллельна

плоскости

Oxy

(перпендикулярна к

оси

Oz ):

Cz D 0

или

z D C;

B 0, C 0

- плоскость

параллельна

плоскости

Oyz

(перпендикулярна к

оси

Ox ):

Ax D 0

или

x D A ;

A 0,

C 0

- плоскость

параллельна

плоскости

Oxz

(перпендикулярна к

оси

Oy):

By D 0

или

y D B;

100

D 0 - плоскость проходит через начало координат.

Пример 3.9. Составить:

а) уравнение плоскости Oxz ;

б) уравнение плоскости, проходящей через ось Ox и точку

M0 2;6; 3 .

Решение:

а) так как искомая плоскость P совпадает с плоскостью


Oxz (т.е.	параллельна ей),		то A 0, C 0. Кроме того, она
проходит через начало координат и, значит, D 0. В результате
получаем уравнение плоскости Oxz:By 0 или y 0;
б) так как плоскость проходит через ось Ox , то A 0 и
D 0 (почему?). Таким			образом,	уравнение плоскости P,
проходящей через ось Ox , имеет				вид: By Cz 0. Точка
M0 P ,	поэтому ее	координаты		2;6; 3 удовлетворяют
уравнению	плоскости:	6B 3C 0		или C 2B. Положим
B 1, тогда C 2 и искомое уравнение P:y 2z 0.
Ответ: а) POxz : y 0;			б) P:y 2z 0.

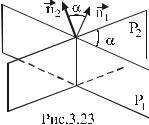
3.3.6. Угол между двумя плоскостями

Угол между плоскостями P1 и P2 (рис. 3.23):

P1 :A1x B1y C1z D1 0,

P2 :A2x B2y C2z D2 0

равен углу, образованному векторами

нормалей n1 и n2 к плоскостям P1 и

P2 , и может быть найдет в результате по формуле

101

					cos			n1,n				2				(3.40)
					cos											(3.40)
								n1			n2
или в скалярной форме
cos		A1A2 B1B2 C1C2											.			(3.41)
cos													.			(3.41)
		A2 B2 C2				A2 B2				C2
1			1		1	2		2				2
Пример 3.10. Найти угол между плоскостями
	P1 :2x y 3z 1 0; P2 :x 3y 5 0.
Решение. Имеем			n1 2; 1;3 ; n2									1;3;0 .		Применяя
формулу (3.41), получаем
	2 1 1 3 3 0													1
cos									и	arccos							.
cos									и	arccos							.
	22 1 2 32			12 32 0											2 35
Ответ: arccos					1		.

				2	35
				2	35

3.3.7. Прямая в пространстве

Рассмотрим два основных способа задания прямой в пространстве.

1. Общими уравнениями:

x B

y C z D 0,

(3.42)

A2x B2y C2z D2 0,

т.е. прямая L задается как

линия пересечения двух

плоскостей P1

и P2

(рис. 3.24).

1 / 21 2 > Следующая >>>

Соседние файлы в папке For Exam

#
15.04.2015224.95 Кб22Несобственные интегралы 2.pdf
#
15.04.2015216.84 Кб17Несобственные интегралы.pdf
#
15.04.2015203.21 Кб15Определенный интеграл.pdf
#
15.04.2015368.26 Кб16Определители.pdf
#
15.04.2015338.66 Кб19Приложения определенного интеграла.pdf
#
15.04.2015324.83 Кб19Прямая и плоскость в пространстве 1.pdf
#
15.04.2015205.01 Кб21Прямая и плоскость в пространстве 2.pdf
#
15.04.2015414.48 Кб38Прямая на плоскости и кривые второго порядка.pdf
#
15.04.2015269.87 Кб17Решение СЛАУ.pdf
#
15.04.2015434.68 Кб26Тройные интегралы 2.pdf
#
15.04.2015488.72 Кб26Тройные интегралы.pdf