
For Exam / Прямая на плоскости и кривые второго порядка
.pdf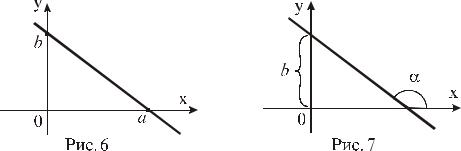
Прямая на плоскости. Алгебраические кривые второго порядка I. Прямая на плоскости
Основные теоретические сведения. Прямая на плоскости в декартовой прямоугольной системе координат 0xy может быть задана уравнением одного из следующих видов:
Общее уравнениепрямой |
|
|
|
|
|
|
||||
|
|
Ax By C 0. |
(3.1) |
|||||||
Уравнение прямой, проходящей через точку M x0,y0 , перпендикулярно |
||||||||||
к нормальному вектору |
|
А;В |
|
|
|
|
|
|
||
N |
|
|
|
|
|
|
||||
A(x x0) B(y y0) 0. |
(3.2) |
|||||||||
Каноническое уравнение прямой, проходящей через точку |
M x0,y0 , |
|||||||||
параллельно направляющему вектору |
|
(m;n) |
|
|||||||
S |
|
|||||||||
|
|
|
x x0 |
|
y y0 |
. |
(3.3) |
|||
|
|
|
|
|
||||||
|
|
|
m |
|
|
|
n |
|
||
Параметрические уравнения прямой |
|
|||||||||
|
|
|
x x0 |
mt, |
(3.4) |
|||||
|
|
|
|
nt. |
||||||
|
|
|
y y0 |
|
||||||
Уравнение прямой в отрезках, где а и b - величины направленных отрезков, отсекаемых прямой на координатных осях 0x и 0y cоответственно (рис. 6):
x |
y |
1. |
|
(3.5) |
a |
b |
|
|
|
Уравнение прямой с угловым коэффициентом, где k tg , |
- |
угол |
||
наклона прямой к оси 0x, b - величина отрезка, отсекаемого прямой на оси
0y (рис.7):
y kx b. |
(3.6) |
Уравнение прямой с угловым коэффициентом k, проходящей через точку M0 x0,y0 :
y y0 k(x x0). |
(3.7) |
Уравнение прямой, проходящей через точки М1(x1,y1); М2(x2,y2):
|
|
y y1 |
|
x x1 |
. |
(3.8) |
||
|
|
|
|
|
||||
|
|
y2 y1 |
x2 x1 |
|
|
|||
Прямые L1 и L2 |
перпендикулярны, если k1k2 1 0 |
и параллельны, |
||||||
если k1 k2, где k1,k2 |
- угловые коэффициенты этих прямых. |
|||||||
|
Решение типовых задач |
|
|
|||||
Пример 3.1. Дана прямая 3x 5y 1 0. Составить уравнение прямой |
||||||||
L, проходящей через точку M0( 1,2): |
|
|
||||||
а) параллельно данной прямой; |
|
|
|
|
||||
б) перпендикулярно к данной прямой. |
|
|
||||||
Решение. a) Нормальный вектор данной прямой |
|
(3; 5) будет |
||||||
N |
||||||||
перпендикулярен и к прямой L. Воспользовавшись уравнением (3.2), |
||||||||
получим искомое уравнение |
|
|
|
|
||||
|
|
|
3(x 1) 5(y 2) 0 |
|
|
|||
или в общем виде |
|
|
3x 5y 13 0. |
|
|
|||
|
|
|
|
|
||||
б) Вектор нормали |
|
(3, 5) |
к данной прямой и прямая L будут |
|||||
N |
||||||||
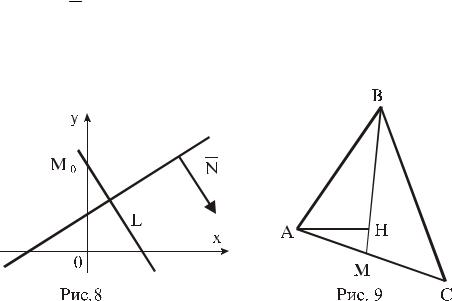
параллельны, так как они перпендикулярны к одной прямой (см. рис. 8). Поэтому вектор N (3, 5) является направляющим вектором прямой L. Используя каноническое уравнение (3.3), получаем уравнение прямой
x 1 |
|
y 2 |
или в общем виде |
5x 3y 1 0. |
|
3 |
5 |
||||
|
|
|
Пример 3.2. Даны вершины треугольника А(1;-1), В(-2;1), С(3;5). Составить уравнение перпендикуляра, опущенного из вершины А на
медиану, проведенную из вершины В. |
|
|
|
|
|||||||||||
|
|
Решение. Пусть ВМ - |
медиана (см. рис. 9), АН ВМ. Вектор |
||||||||||||
|
|
1( |
|
|
|
), |
|
(3; 2), |
|
|
(5;4). Тогда |
|
(4;1). Вектор |
|
|
|
ВМ |
ВА |
ВС |
ВА |
|
ВС |
ВМ |
ВМ |
|||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
является нормальным вектором прямой АН. Точка А(1;-1) принадлежит АН. Воспользовавшись уравнением (3.2), получим уравнение перпендикуляра
|
|
|
|
|
4(x 1)1(y 1) 0 |
или |
4x y 3 0. |
|
|
|
|
|
|
|||||||||||||||||||||||
|
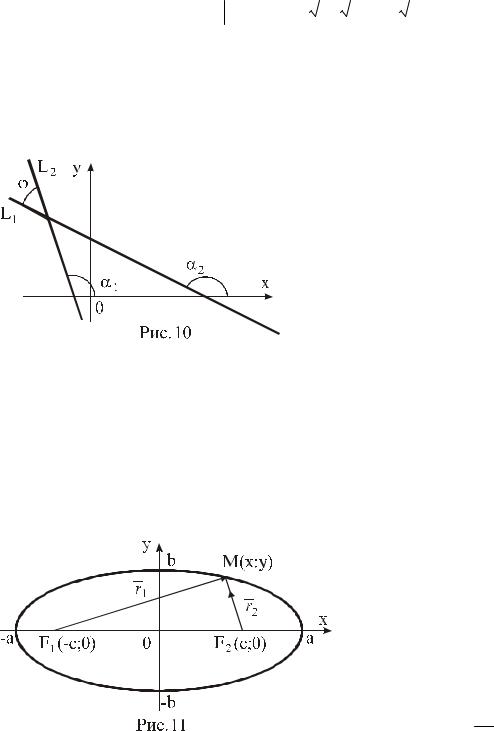
Пример 3.3. Определить угол междудвумя прямыми: |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
5x y 7 0 (L1), 3x + 2y = 0 (L2 ). |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
Решение. Первый способ. |
|
|
|
|
1 (5; 1) |
- нормальный |
вектор прямой |
||||||||||||||||||||||||||||
|
N |
|||||||||||||||||||||||||||||||||||
L1, |
|
2 (3;2)- нормальный вектор прямой L2. Поэтому |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
N |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
cos |
|
1, |
|
2 |
|
|
5 3 |
2( 1) |
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
N |
N |
|
, |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
N1 |
|
N2 |
|
|
|
26 |
13 |
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||||
откуда |
- искомый угол. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Второй способ. Приведем уравнения прямых к виду |
|
y kx b. |
|
||||||||||||||||||||||||||||||||
y 5x 7 (L ), k |
|
5, y=-3x (L |
|
|
), k |
|
3 |
. k |
|
tg |
,k |
|
tg |
|
|
(см. |
||||||||||||||||||||
1 |
|
1 |
2 |
|
|
|
2 |
|
|
|
|
2 |
2 |
|
|
|
1 |
|
|
1 |
|
|
2 |
|
|
|
|
2 |
|
|
||||||
рис.10), |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1, tg = tg( 2 1) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg 2 tg 1 |
|
|
k2 k1 |
. |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 tg 2 tg 1 |
1 k2k1 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для нашей задачи |
3 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg |
|
|
|
|
|
2 |
|
|
|
1, |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 ( |
3) 5 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
. |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
откуда искомый угол |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
II.Алгебраические кривые 2-го порядка Основные теоретические сведения
Вдекартовой системе координат уравнение окружности с центром в точке M(a;b) и радиусом R имеет вид
(x a)2 (y b)2 R2.
Если центр находится в начале координат (a = 0, b = 0), то уравнение окружности
запишется в виде
x2 y2 R2.
Каноническое уравнение эллипса с фокусами на оси 0x:
F1( c,0), F2(c,0) имеет вид xa22 by22 1,
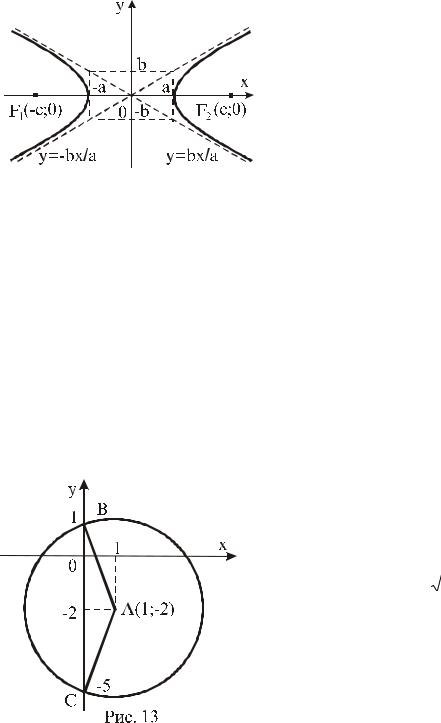
где
а(а>0) – большая полуось, b(b>0) - малаяполуось эллипса,
b2 a2 c2 .
Число e ac называется
эксцентриситетом эллипса.
Каноническое уравнение гиперболы
(рис.12) с фокусами на 0х и
симметричными относительно начала
координат F1( c,0), F2(c,0) имеет вид
x2 y2 1,
a2 b2
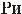
 где b2 c2 a2, a - называется действительной полуосью, b - мнимой полуосью. Уравнения асимптот
где b2 c2 a2, a - называется действительной полуосью, b - мнимой полуосью. Уравнения асимптот
гиперболы y bax.
Уравнения директрис эллипса и гиперболы: D :x a |
; |
D |
2 |
:x a. |
|
1 |
e |
|
|
e |
|
|
|
|
|
||
Каноническое уравнение параболы, фокус F(p2,0) которой находится
на оси 0х, имеет вид y2 2px. Уравнение директрисы: x p2.
Пример 3.4. Вычислить площадь треугольника, одна из вершин которого совпадает с центром, а две другие - с точками пересечения
окружности x2 y2 |
2x 4y 5 0 |
с осью ординат. |
|
|
|
|
|
|
|
|
|
Решение. |
Выделив полные квадраты |
||||||
|
в уравнении |
окружности, |
получим |
||||||
|
уравнение (x 1)2 (y 2)2 10. |
Из |
этого |
||||||
|
уравнения определяем |
координаты |
центра |
||||||
|
окружности |
|
|
|
|
|
|
|
|
|
А(1;-2) и радиус R = |
|
10 |
. |
Координаты |
||||
|
точек В и С (рис. 13) находим из условия |
||||||||
|
|
x 0, уравнениеосиординат, |
|
||||||
|
|
x2 y2 2x 4y 5 0 |
|
|
|||||
|
или |
y2 4y 5 0, y1 |
1, y2 |
5. |
|
||||
|
|
Получим |
точки |
В(0; |
1), |
С(0; -5). |
|||
Площадь треугольника можно найти по формуле S |
|
|
1 |
|
|
|
, |
|
|
или по |
|
|
АВ |
АС |
|||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
формуле S 12ВС h, где h - длина высоты, опущенной из вершины А на сторонуВС, ВС = 6, h = 1, S 3 (кв.ед).
Ответ: S 3 (кв.ед.)
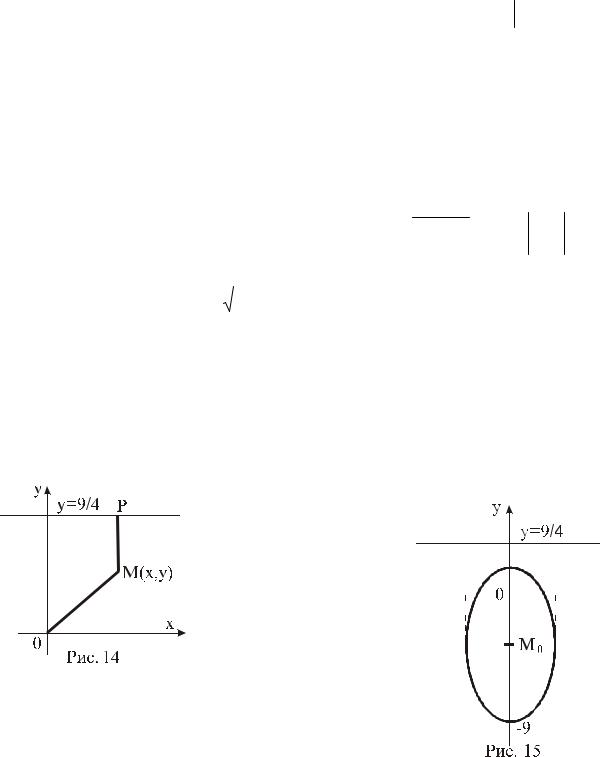
Пример 3.5. Составить уравнение линии, для каждой точки которой отношение расстояния до начала координат к расстоянию до прямой 4y– 9 = 0 равно 4/5. Построить линию.
Решение. Дано: MP0M 54 (см. рис.14), где 0M = 
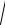 x2 y2 ; МР = y- 94 . Имеем
x2 y2 ; МР = y- 94 . Имеем
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
x |
2 |
y |
2 |
|
y |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
5 |
4 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
или |
|
|
|
|
|
|
|
9 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
y |
2 |
|
16 |
|
x |
2 |
y |
2 |
|
|
16 |
8 9 |
y |
81 |
0 |
|||||||||||
|
|
25 |
y |
|
|
|
1 |
25 |
|
25 |
25 |
|||||||||||||||||
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
x |
2 |
9 |
y2 8y 16 16 |
|
81 |
|
0 |
|
x2 |
|
y 4 2 |
1. |
||||||||||||||
|
|
|
|
|
25 |
|
|
|
|
25 |
9 |
|
25 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Полученное уравнение является
уравнением эллипса с центром в точке
М0(0;-4) и полуосями  a = 3, b = 5 (см. рис.15).
a = 3, b = 5 (см. рис.15). 

Ответ: x2 (y 4)2 1. 9 25
