
For Exam / Элементарные методы интегрирования
.pdf§ 1. ЭЛЕМЕНТАРНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ
Пусть |
функция |
f x |
определена |
на |
некотором интервале |
|||
a,b . Тогда |
функция |
F x |
называется |
первообразной для |
||||
функции |
f x |
|
|
|
|
|
|
f x для всех |
на интервале a,b , если F x |
||||||||
x a,b . |
|
|
|
|
F x |
|
|
|
Теорема. |
Если |
функция |
является |
первообразной |
||||
функции |
f x |
на a,b , |
то множество всех первообразных для |
|||||
f x задается формулой F x С , где С – некоторое постоянное число.
Определение. Совокупность всех первообразных для функции
f x называется неопределенным интегралом от функции |
f x и |
|||
обозначается символом f x dx. |
|
|
||
Таким |
образом, если F x - какая-либо первообразная |
|||
функции f x , то |
f x dx F x С . |
f x - |
||
Знак |
называется знаком неопределенного интеграла, |
|||
подынтегральной |
функцией, |
f x dx - подынтегральным |
||
выражением.
Основные правила интегрирования
Везде далее предполагается, что все рассматриваемые интегралы существуют.
I. |
dF x F x C. |
||
II. |
d f x dx f x dx. |
||
III. |
f x dx f x dx, где const . |
||
IV. |
f x g x dx f x dx g x dx. |
||
V. |
Если f x dx F x С и a 0, то |
||
|
f ax b dx |
1 |
F ax b C . |
|
|
||
|
|
a |
|

Таблица основных интегралов
1. x dx |
|
x 1 |
|
C 1 . 2. |
dx |
ln |
|
|
|
x |
|
|
|
C . |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
dx x C . |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
В частности, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
3. axdx |
|
ax |
|
|
|
C . |
4. exdx ex C. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
lna |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
5. sin xdx cosx C . |
6. cosxdx sin x C . |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
7. |
|
dx |
|
|
tgx C . |
8. |
|
|
|
|
dx |
|
|
ctgx C. |
|
||||||||||||||||||||||||||||||||||||||||
cos2 x |
sin2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
9. tgxdx ln |
|
cosx |
|
C . |
10. ctgxdx ln |
|
sinx |
|
C . |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
11. |
|
|
dx |
|
|
arctgx C . |
12. |
|
|
|
|
dx |
|
|
|
|
1 |
|
arctg |
x |
C . |
||||||||||||||||||||||||||||||||||
1 x2 |
|
|
a2 x2 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
a |
|
|||||||||||||||||||||
13. |
|
|
dx |
|
|
|
|
|
arcsinx C. |
14. |
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
arcsin |
x |
C. |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
1 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 x2 |
|
|
a |
|
||||||||||||||||||||||||||||||
|
|
|
dx |
|
|
|
|
1 |
|
|
a x |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
15. |
|
|
|
|
|
|
|
ln |
C.16. |
|
|
|
|
|
|
|
|
|
ln |
x |
x2 a2 |
C. |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
a2 x2 |
2a |
|
a x |
|
|
|
|
|
|
|
x2 a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
17. |
chxdx shx C. |
18. shxdx chx C. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
19. |
|
dx |
|
thx C . |
20. |
|
|
dx |
|
|
cthx C . |
|
|||||||||||||||||||||||||||||||||||||||||||
ch2x |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sh2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Рассмотрим примеры применения таблицы и основных правил интегрирования.
|
2 |
|
1 |
|
|
|
Пример 1.1. Вычислить интеграл I= x |
|
x 3 1 |
|
|
|
dx. |
|
|
|
|
|||
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
x |
||
Решение. Перемножим многочлены, стоящие под интегралом:
|
|
x |
2 |
|
|
x |
|
|
3 |
|
|
1 |
|
||||
|
|
|
|
|
|
|
|
|
|
||||||||
I= x2 |
x 3 |
|
|
|
|
|
|
dx. Заменив |
x на x2 |
, |
|||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
x |
|
x |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
x |
|
|
|
|
||||||||
преобразуем выражение под интегралом:

|
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
||||||||||
|
|
I= |
|
x |
x 3 x |
2 |
|
x |
2 |
3x |
|
2 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx. |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Применим правила III и IV, после чего воспользуемся |
|||||||||||||||||||||||||||||||||||||
формулой 1 таблицы интегралов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
I= x2dx xdx 3 dx x2dx x2dx 3 x 2dx= |
|||||||||||||||||||||||||||||||||||||
|
x2 1 |
|
x1 1 |
|
|
|
3 |
1 |
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
1 |
1 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
x |
|
|
|||||||||||||||||||
= |
|
3x |
|
x2 |
|
|
|
|
2 |
|
|
|
3 |
|
2 |
|
C= |
||||||||||||||||||||
2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||||||||||||||||
|
1 1 |
|
3 |
1 |
|
1 |
|
1 |
|
|
|
|
1 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
2 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
x3 |
|
|
|
|
|
x2 |
|
|
|
2 |
|
|
|
x5 |
|
|
|
|
2 |
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3x |
|
|
|
|
|
|
|
6 x C. |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
5 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
1 |
|
|
|
x |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xdx. |
|
||||||||||||||||||||||||||||
|
Пример 2.1. Найти интеграл 2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Решение. Раскроем скобки в подынтегральном выражении, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
воспользуемся свойством IV и таблицей интегралов (формулы 1 и |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
x |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
x |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
xdx= |
|
|
|
|
x |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
dx = |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 x3 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
= |
|
2x dx= x |
|
dx 2xdx= |
x2 1 |
|
|
2x |
|
C= |
|
|
C. |
|||||||||||||||||||||||||||||||||||||||||||||
|
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
ln2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
ln2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Пример 3.1. 3x 2 11dx. |
|
|
|
|
|
|
|
|
|
|
|
|
|
a 3, |
|
|
|
b 2 |
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
Решение. Применим свойство V |
|
|
|
и формулу 1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
таблицы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x 212 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x 211dx= |
1 |
|
C. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||

Пример 4.1. sin2 xdx. |
|
|
|
|
|
|
|
|
|
||||||||
Решение. Применим формулу понижения степени: |
|
|
|||||||||||||||
sin2 x |
1 cos2x |
. |
По свойствам III, |
V и по формулам 1, 6 |
|||||||||||||
|
|
||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
sin2 xdx= |
1 cos2x |
dx= |
1 |
|
dx cos2xdx = |
1 |
x |
||||||||||
|
|
2 |
2 |
2 |
|||||||||||||
|
|
|
|
|
|
|
|
x |
|
sin2x |
|
|
|||||
|
|
1 |
|
1 |
sin2x C |
|
|
C . |
|
|
|||||||
|
|
2 |
2 |
|
|
|
|||||||||||
2 |
|
|
|
|
|
|
4 |
|
|
|
|||||||
dx
Пример 5.1.  .
.
 25 9x2
25 9x2
Решение. Так как 
 25 9x2
25 9x2 
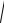 52 3x 2 , то при вычислении
52 3x 2 , то при вычислении
интеграла воспользуемся свойством V и формулой 14 таблицы интегралов:
|
|
dx |
= |
|
dx |
= |
1 |
arcsin |
3x |
C. |
|
|
|
|
|
5 |
|||||
|
|
25 9x2 |
|
|
52 3x 2 |
3 |
|
|||
dx
Пример 6.1.  .
.
 x 2
x 2  x 3
x 3
Решение. Освободимся от иррациональности в знаменателе, для чего умножим и числитель, и знаменатель дроби на выражение

 x 2
x 2 
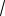 x 3 :
x 3 :
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
x 2 |
|
x 3 |
|
|
|
|
|
|
= |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 x 3 x 2 |
x 3 |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x 2 x 3 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x 2 |
x 3 |
|
|
|
|
|
|
x 2 |
x 3 |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
= |
|
|
|
|
|
|
|
|
|
dx = |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
x 2 x 3 |
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x 2 |
|
x 3 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||||
|
1 |
x 2 |
x 3 dx= |
1 |
|
x 2 |
|
dx |
1 |
x 3 |
|
dx= |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
5 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
1 |
|
2 |
|
|
|
1 |
|
2 |
|
|
C = |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
= |
|
|
x 2 3 |
x 3 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
5 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||

|
2 |
|
|
|
2 |
|
|
C . |
|
= |
x 2 3 |
x 3 3 |
|||||||
|
|
||||||||
15 |
15 |
|
|
||||||
x2dx
Пример 7.1. x2 1.
Решение. Под интегралом стоит неправильная дробь, так как степень числителя равна степени знаменателя. Выделим у дроби целую часть. Для этого можно поделить числитель на знаменатель по правилу деления многочлена на многочлен или в дроби
x2dx
преобразовать числитель, прибавляя и вычитая 1: x2 1=
|
x |
2 |
1 1dx |
|
2 |
1 |
|
|
1 |
|
|
|
|
|||||||||
|
|
x |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
dx= |
|
|
|
|
|
|
x |
2 |
1 |
|
2 |
1 |
|
x |
2 |
1 |
|
|
|
|||||||
|
|
|
|
x |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
dx |
||||
|
|
|
|
|
= 1 |
|
|
|
|
|
dx= dx |
|
|
|
= x arctgx C . |
|||||||
|
|
|
|
|
|
|
|
|
|
x2 |
|
|||||||||||
|
|
|
|
|
|
|
x2 1 |
|
|
|
|
|
|
1 |
||||||||
dx
Пример 8.1. x2 4x 13.
Решение. Квадратный трехчлен не имеет действительных корней, так как его дискриминант D=-4<0. Выделим в
знаменателе полный квадрат: x2 4x 13 x2 |
4x 4 9 |
||||||||||||||||||||||||||||||||||||||||
x 2 2 9. Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
dx |
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
dx |
1 |
|
|
x 2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arctg |
|
C. |
|||||||
|
x2 4x 13 |
x 2 2 |
9 |
x 2 2 |
32 |
3 |
3 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
Пример 9.1. |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
Решение. |
|
|
9x2 6x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
dx |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
9x2 6x 1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
9x2 6x 2 |
|
|
|
1 |
|
|
|
|
3x 1 2 1 |
||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
ln3x 1 |
|
3x 1 2 1 |
C |
ln3x 1 |
|
|
|
9x2 6x 2 |
C. |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||

Пример 10.1. sin 2x cosxdx.
Решение. Справедлива формула
|
|
sin cos |
1 |
sin sin . |
|||||||||
|
|
|
|
|
|||||||||
|
|
|
|
2 |
|
|
|
|
|
||||
Тогда sin 2x cosxdx= |
1 |
|
sin 2x x sin 2x x dx= |
||||||||||
2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||
= |
1 |
sin3x sinx dx= |
|
1 |
|
1 |
cos3x |
1 |
cosx C = |
||||
2 |
|
2 |
|
|
|||||||||
|
|
|
|
|
3 |
2 |
|
||||||
=1cos3x 1cosx C. 6 2
Замечание. При вычислении интегралов полезно использовать и другие формулы тригонометрии:
|
|
|
|
|
1 tg2x |
|
1 |
|
, |
1 ctg2x |
1 |
|
, |
|
|
|
||||||||||
|
|
|
|
cos2 |
|
sin2 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
x |
|
|
||||||||||
|
|
|
|
|
sin2 x |
1 cos2x |
, |
cos2 x |
1 cos2x |
, |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||
|
|
|
|
|
cos cos |
|
1 |
cos cos , |
||||||||||||||||||
|
|
|
|
2 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
sin sin |
1 |
cos cos . |
|
|
|||||||||||||||||
|
|
|
|
2 |
|
|
||||||||||||||||||||
Пример 11.1. tg2xdx. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||||||||||||
Решение. Воспользуемся формулой 1 tg2x |
|
, откуда |
||||||||||||||||||||||||
cos2 |
|
|||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
||||
tg2x |
|
|
|
1. В результате интеграл примет вид: |
|
|
||||||||||||||||||||
cos2 |
|
|
|
|||||||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
||||||
|
|
2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
tg |
|
xdx |
|
1 dx |
|
|
dx tgx x C . |
|||||||||||||||||||
|
|
cos2 |
|
|||||||||||||||||||||||
|
|
|
|
|
cos2 x |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
||||||
