10. Формула полной вероятности. Формула Байеса.

Гипотезы образующие полную группу событий.

А может наступить совместно с одной из гипотез.

А=А+…+А

Р(А)=Р(А+…+Р(А=Р(+ Р(+..+ Р(=>

Р(А)=- формула полной вероятности

Рассмотрим i-тое слагаемое в правой части в формуле полной вероятности

Р(А =>

формула Байсса

По формуле осуществляется переоценка вероятности гипотез при условии, что событие А наступило.

Р(, i=, n- априорные вероятности

Р(Аi=, n- апостериорные вероятности

11. Дискретные случайные величины. Формы задания их законов распределения.

Случайной величиной наз-ся функция которая задана на множестве элементарных исходов или в пространстве элементарных событий.

x,y,z - элементарный исход множество достоверных событий.

x=f (w) w-

Различают дискретные и непрерывные случайные величины ( курс валют, количество студентов на парах)

Случайная величина наз-ся дискретной если ее возможныe значения изолированы друг от друга и образуют конечное или бесконечное множество, которое является всегда счетным.

Случайная величина наз-ся непрерывной если ее возможные значения не непрерывно заполняют некоторый интервал на оси.

Закон распределения случайной величины дает исчерпывающую характеристику.

Законом распределения случайных величин наз-ся всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующим им вероятностями.

Закон распределения ДСВ можно задать на основе ряда распределения и функции распределения.

Ряд распределения - Это таблица, состоящая из 2ух строк, в 1ой из которых указаны возможные значения случайной величины, во 2ой соответствующие им вероятности.

xi	X1	X2	...	Xn	...
pi	P1	P2	...	Pn	...

Pi - вероятность того, что случайна величина X=Xi

pi=p(x=xi) , i=1,2...

Событие X=xi; i=1,2... образуют полную группу событий

Графическое изображение ряда распределения - многоугольник распределения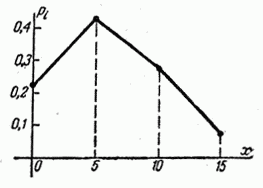

Функция распределения СВ - это вероятность того, что СВ x принимает значение меньше текущей величины x

F(x)=P(X<x)

1. F(x) - неубывающая функция

2.F(-

3.F(+

Функция распределения СВ является ступенчатой.

При чем величина i-той ступеньки равна p(X=xi) вероятности того, что X=i-тому значению.

Функция распределения непрерывна слева.

21. Точные законы распределения. Распределение («хи-квадрат»)

Пусть мы имеем n независимых сл.величин ,, … , , каждая из которых распределена по закону Гаусса. Сформируем сл.величину по след.правилу: =

Величина также является случайной и непрерывной. Аналитическое выражение функции плотности распределения сл.величины имеет вид

f() =

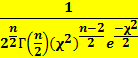
Распределение имеет только один «точный» параметр n – число степеней свободы.

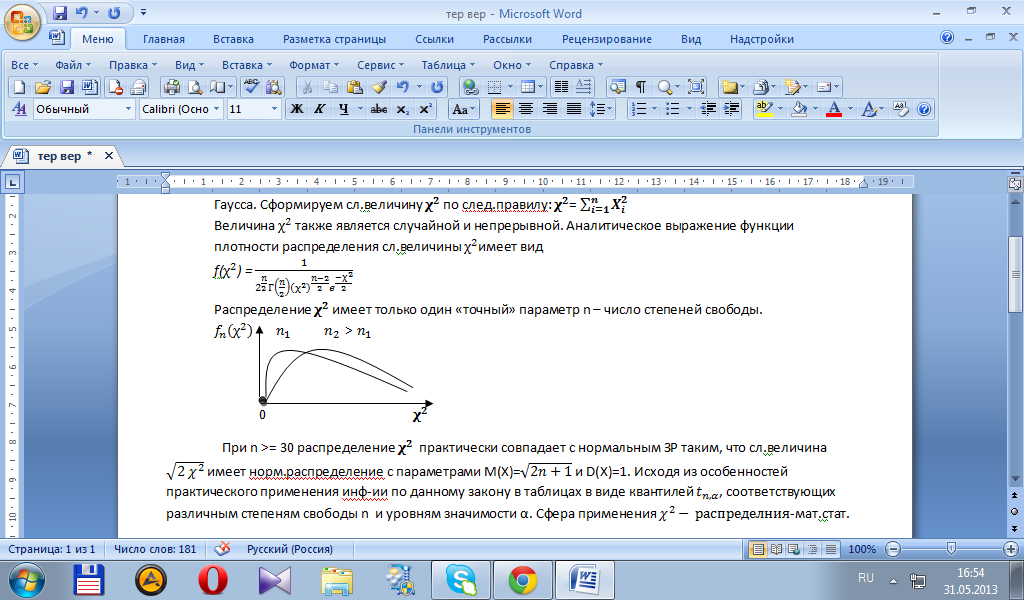
При n >= 30 распределение практически совпадает с нормальным ЗР таким, что сл.величина имеет норм.распределение с параметрами M(X)= и D(X)=1. Исходя из особенностей практического применения инф-ии по данному закону в таблицах в виде квантилей , соответствующих различным степеням свободы n и уровням значимости α. Сфера применения -мат.стат.

22. Точные законы распределения.Распределение Стьюдента.

Пусть мы имеем сл.величину V, распределенную по закону с n степенями свободы. Так же задана сл.величина Z, распределенная по закону Гаусса. Сл.величины V и Z независимы. Новая сл.величина Т создается по формуле Т=. Получившийся в результате ЗР величины Т получил название распр-е Стьюдента. Функция плотности этого распр-я имеет вид:

Параметр n обозначает число степеней свободы. Графики функций расп-я Стьюдента для различных степеней свободы

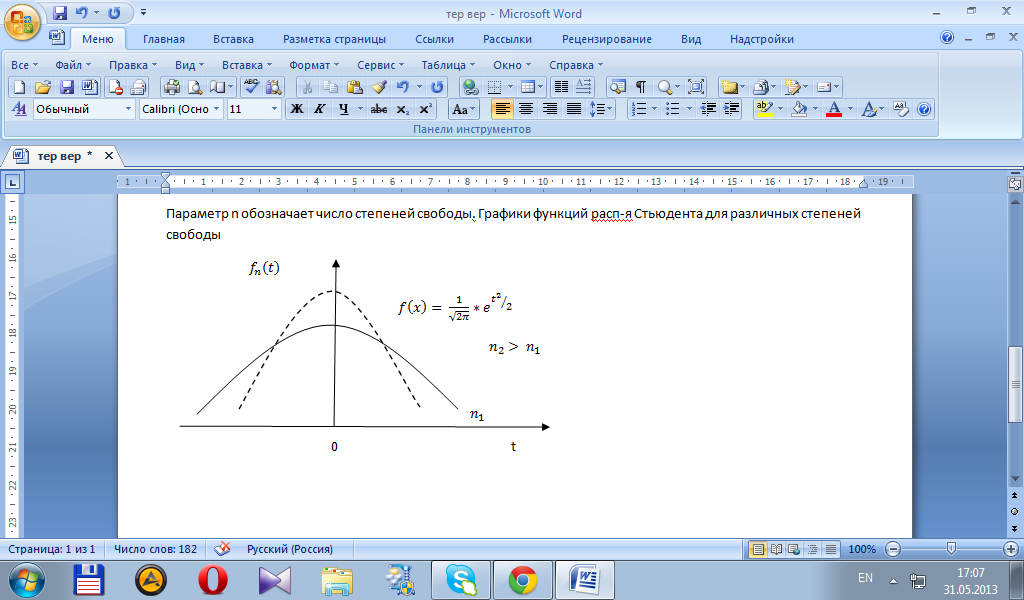
C увеличением n кривая расп-я Стьюдента приближается к кривой расп-я Гаусса. При n >=30 практически происходит их полное слияние. Таблич.инф-ия по закону Стьюдента представлена в виде квантилей для различных степеней свободы n и разных уровней значимости α. Основная сфера применения – мат.стат.