7.Простые и сложные события. Произведение событий. Условная вероятность события. Теорема умножения вероятностей.
Произведением нескольких событий называется событие, состоящее в совместном наступлении всех этих событий.
Условная
вероятность события B
- это полученная вероятность события
B,
найденная при условии, что событие A
произошло. Обозначается 
(B)
или P(B/A)
Теорема умножения вероятностей.
Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, найденную в предположении, что первое событие произошло.
Док-во:
пусть n-число
равновозможных исходов эксперимента
по воспр-ию соб.А и В. Из них m
исходов способств.А(m~A),
k~B,
l~AB.
;
;
.
Рассм.усл.вер.соб.А
при В наступившим: 
⇒
⇒
условная вер.соб.В при А наступившем
Теорема умножения для несовм.событий
Вероятность произведения независимых событий равна произведению вероятностей этих событий
A и B-независимые.
8. Формула Бернулли. Формула Пуассона. Сфера их применения.
Формула Бернулли
Т-ма: Если вероятность p наступления события A в каждом испытании постоянна, то вероятность P k,n того, что событие А наступит k раз в n независимых испытаниях равна:
где q = 1-p
В формуле Бернулли используется число сочетаний. Для реализации схемы Бернулли необходимы два условия: 1) независимость проводимых испытаний; 2) p = const Распределение вероятностей в схеме Бернулли - биномиальное.
Применяется при решении задач на нахождение вероятности возможного числа появления бракованных деталей; в задаче с условием найти количество подбросов игральной кости, при заданном наивероятнейшем выпадении
Формула Пуассона
Применяется в случае, когда мы хотим вычислить вероятность Pm,n появления события A при большом числе испытаний n, например P300,500. Например, найти вероятность того, что из 1825 студентов 1ое сентября будет днем рождением одновременно четырех студентов. По формуле Бернулли вычисление технически сложно.
Для больших n есть так называемые асимптотические формулы. Наиболее простой из них является теорема Пуассона.
Т-ма: Если вероятность p наступления события А в каждом испытании стремится к нулю при неограниченном увеличении числа n испытаний, причем произведение np стремится к постоянному числу λ, то вероятность Pm,n того, что событие A появится m раз в n независимых испытаниях, удовлетворяет предельному равенству
Приближенная формула Пуассона:
9.Локальная и интегральная теоремы Муавра-Лапласа.
Локальная Теорема.
Если
вероятность p
наступления события А в каждом испытании
постоянна и отлична от 0 и 1,то вероятность
P(m,n)
того, что событие А произойдет m
раз в n
независимых испытаниях при n
достаточно больших, приближенно равна
;
g=1-р
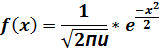
Гауссовая
кривая
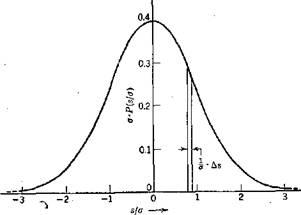
f(-x)=f(x)-свойство четной функции
Существует
таблица значений функций f(x)для
x
[0;5]
при x
>=5 f(x)
Интегральная теорема.
Если
вероятность P
наступления события A
в отдельных испытаниях постоянна и
отлично от 0 и 1, то вероятность того, что
число m
наступления события A
в n
Независимых испытаниях заключено в
пределах от A
до B
включительно при достаточно большом
числе испытаний n
приблизительно равна 
Следствие. Если вероятность P наступления события А в отдельных испытаниях постоянна и отлична от 0 до 1, то при достаточно большом числе n независимых испытаний вероятность того что,
а)
число m
наступления события А отличается от
произведения np
не более чем на величину E>0
приближенна равна p(
б)Частота
события А в n
независимых испытаниях заключена в
пределах от α До β включительно приближенна
равна P(α
z1=
;
z2= 
В)
частота 
отличаются от вероятности (p)
его наступления в отдельном испытании
на величину ∆≥0 по абсолютной величине
приближенно равна
)