6.5 Задачі для самостійного розв’язання

1.Нехай.Знайдіть

2.Знайдіть добуток перестановок і запишіть його у вигляді:

.

1) ;

2) .

3.Задані престановки,,,. Знайти добутки: 1), 2), 3), 4), 5), 6), 7), 8), 9), 10), 11), 12).

4.Розкладіть у добуток незалежних циклів і транспозицій перестановки. Знайдіть їх порядок. Зазначте, які з них є парними, які – непарними.

1) ; 2);

3) ; 4);

5) .

5.Знайдіть, якщо.

6.Знайдіть усі перестановки множинипереставні з перестановкою, якщо.

7.Знайдіть порядки всіх елементів групи. Чи є групациклічною?

8.З’ясуйте, чи буде підгрупою множина всіх елементів другого порядку в групі.

9.Побудувати множинупарних перестановок у групі. Чи буде множинапідгрупою в групі?

10. Знайти всі підгрупи в групах 1), 2)(група парних перестановок у групі).

11. Вкажіть найвищій порядок перестановки в групі 1); 2); 3); 4); 5); 6). Наведіть приклад перестановки цього найвищого порядку, з’ясуйте, чи буде вона парною.

12.Навести приклади перестановок з групипорядку 1) 10; 2) 4; 3) 6; 4) 5; 5) 12.

13.Нехай задано розклад перестановки в добуток незалежних циклів.... Знайти розклад перестановкиу добуток незалежних циклів.

14. Скільки елементів порядку 6 міститься в групі 1), 2)?

15. Довести, що порядок непарної перестановки є парним числом.

16.Знайдіть порядки всіх елементів групи обертань правильного-кутника, якщо 1); 2); 3); 4); 5); 6). Чи будуть ці групи циклічними?

17.Знайдіть усі утворюючі елементи групи обертань правильного-кутника, якщо 1); 2); 3); 4); 5); 6).

18.Знайдіть усі підгрупи групи обертань правильного-кутника, якщо 1); 2); 3); 4); 5); 6).

19.Знайдіть усі підгрупи групи симетрій 1) правильного трикутника; 2) квадрата; 3) ромба, який не є квадратом; 4) прямокутника.

7 Гомоморфізм груп

7.1 Мета заняття

Навчити студентів перевіряти гомоморфність конкретних відображень; описувати ядро та образ гомоморфізму в термінах даної задачі; встановлювати деякі властивості гомоморфізмів.

7.2 Методичні вказівки з організації самостійної роботи

Студент повинен: знати поняття ізоморфізму, властивості груп (одиниця переходить в одиницю, обернене відображення теж є ізоморфізмом); теорему Келі, поняття автоморфізму групи, гомоморфізму; вміти розв’язувати задачі за темою [3, c. 156-163].

7.3 Контрольні запитання

1. Що називається гомоморфізмом; ізоморфізмом; автоморфізмом; мономорфізмом, епіморфізмом?

2. Чим відрізняється ядро гомоморфізму від ядра ізоморфізму?

7.4 Приклади розв’язання аудиторних задач

Приклад 1.Доведіть, що адитивна група дійсних чисел ізоморфна мультиплікативній групі додатних дійсних чисел.

Розв’язок. Для доведення розглянемо відображення

, де , ата.

Спочатку потрібно перевірити, що відображення буде гомоморфізмом, тобто зберігається групова операція. Якщо задані групи та, та є відображення, то має виконуватися умова.

Переконуємося, що для :, тобто відображення– гомоморфізм.

Знайдемо ядро гомоморфізму. За визначенням, ядром гомоморфізму називається множина елементів .

.

Оскільки ядро складається з одного елемента , це означає, що відображення ін’єктивне.

Визначимо образ відображення. Образом називається множина елементів вигляду .

.

Образ відображення співпадає з множиною елементів з другої групи , тому відображення сюр’єктивне. Отже, відображенняводночас і ін’єктивне тасюр’єктивне, тому воно – бієктивне. Робимо висновок, що відображення – ізоморфізм. Коротко це записується так:.

Приклад 2.Довести, що відображення є гомоморфізмом. Знайти його ядро й образ.

Розв’язок. Маємо:. Тобто,f-гомоморфізм., тобто– множина коренівn-го степеня з 1. Відображення неін’єктивне. Знайдемо образ. Підносячи комплексні числа до степеня, отримуємо множину комплексних чисел. Отже,. Відображення сюр’єктивне. Висновок:f-епіморфізм.

Приклад 3.Чи буде перетворенняповної лінійної групи, автоморфізмом?

Розв’язок. Для автоморфності (як і гомоморфності) перетворення необхідно, щоб була виконана умова. У нашому випадку. Висновок:– не автоморфізм.

Приклад 4.Довести, що відображення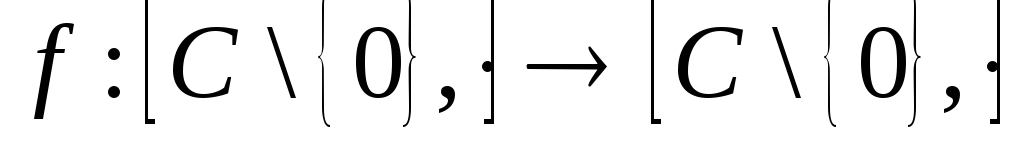,є гомоморфізмом. Знайдіть його ядро й образ.

Розв’язок. Позначимо, та.

Нехай , тоді. Отже,– гомоморфізм. Знайдемо

–одиничне коло. Відображення неін’єктивне.

. Відображення несюр’єктивне. Висновок: – гомоморфізм.

Приклад 5.Знайдіть усі гомоморфізми циклічної групипорядку 6 у циклічну групупорядку 18.

Розв’язок.Розглянемо групи , , відображення. Використауємо властивість, що одиничний елемент однієї групи відображується в одиничний елемент іншої групи. З огляду, що, маємо,,,,, отримуємо можливі образи утворюючого елемента. Число гомоморфізмів дорівнює шістьом.

Приклад 6.Знайдіть усі гомоморфізми циклічної групипорядкуу себе.

Розв’язок. Гомоморфізм цілком визначається образом утворюючого елемента. А оскільки образом утворюючого елемента може бути будь-який елемент групи, то число гомоморфізмів дорівнює.

Приклад 7.Знайдіть усі гомоморфізми циклічної групипорядку 18 у циклічну групупорядку 6.

Розв’язок. Відомо, щота, а також. Тоді можливі образи утворюючого елемента.