Міністерство освіти і науки україни

ХАРКІВСЬКИЙ НАЦІОНАЛЬНИЙ

УНІВЕРСИТЕТ РАДІОЕЛЕКТРОНІКИ

МЕТОДИЧНІ ВКАЗІВКИ

до практичних занять

з дисципліни

«АЛГЕБРА та ГЕОМЕТРІЯ»

Частина 2

для студентів денної форми навчання напрямів:

6.040301 – Прикладна математика,

6.040303 – Системний аналіз,

6.040302 – Інформатика

1. ЗАТВЕРДЖЕНО

кафедрою прикладної математики.

Протокол №7 від 15.01.13.

Харків 2013

Методичні вказівки до практичних занять з дисципліни „Алгебра та геометрія”.Ч. 2 для студентів денної форми навчання напрямів 6.040301 – Прикладна математика, 6.040303 – Системний аналіз, 6.040302 – Інформатика / Упоряд.: А.Д. Тевяшев, Н.Б. Манчинська. – Харків: ХНУРЕ, 2013. – 52 с.

Упорядники: А.Д. Тевяшев,

Н.Б. Манчинська

Рецензент О.Г. Руденко, д-р. техн. наук, професор каф. ЕОМ ХНУРЕ

ЗМІСТ

Вступ 4

1  Множина комплексних чисел. Дії з комплексними числами 4

2 Бінарні алгебраїчні операції 9

3 Основні властивості груп 12

4Підгрупи 16

5 Циклічні групи 21

6 Перестановки 24

7 Гомоморфізм груп 27

8 Суміжні класи 31

9 Фактор-групи 34

10 Основні властивості кілець і полів 36

11 Гомоморфізм кілець. Ідеали 41

12 Операції над ідеалами. Фактор-кільця 43

13 Кільце лишків. Алгоритм Евкліда 46

Термінологічний словник 50

Рекомендована література 51

вступ

Алгебра займає особливе місце в математичній освіті студентів. Поряд з функціональним аналізом, алгебра – це мова сучасної математики. Поняття й результати цього курсу використовуються під час вивчення інших предметів.

Незважаючи на свій елементарний характер, початковий курс алгебри являє певні труднощі для засвоєння через формальний характер мислення. Студент стикається з необхідністю міркувань у рамках заданих, і при тому різноманітних, систем аксіом. Тому на практичних заняттях слід приділяти головну увагу задачам, які вимагають логічних міркувань, де розв'язок чітко обґрунтований. З урахуванням цієї вимоги відібрані задачі даних методичних вказівок.

Особливість дисципліни – наявність великої кількості нових понять, необхідних під час розв'язання задач.

Зв'язок між темами занять вельми послідовний.

1 Множина комплексних чисел. Дії з комплексними числами

1.1 Мета заняття

Розглянути алгебраїчну, тригонометричну, показову форму комплексного числа, зв'язок між цими формами. Навчити студентів виконувати дії з комплексними числами.

1.2 Методичні вказівки з організації самостійної роботи

За цією темою студент повинен знати: поняття комплексного числа, різні форми його подання, вміти виконувати дії з комплексними числами, зображувати графічно комплексні числа на площині [1, c. 205-209]; вміти використовувати теоретичні знання під час розв'язання задач за темою.

1.3 Контрольні запитання та завдання

1. Покажіть зв'язок між різними формами комплексного числа.

2. Як зображуються комплексні числа на площині?

1.4 Приклади розв'язання аудиторних задач

Приклад 1. Доведіть рівності:

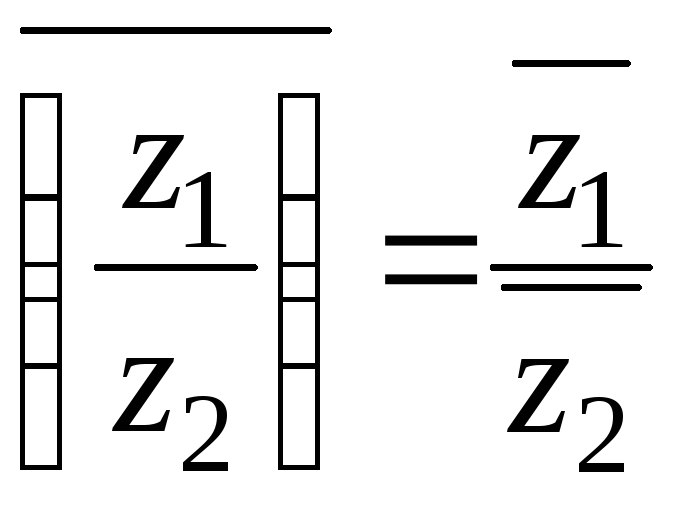1) ; 2) ; 3) , ; 4) .

Розв'язок. 1. Нехай , де та , тоді . Розглянемо , тобто .

2. Нехай , а , тоді . Розглянемо  , тобто .

3. Нехай , , тоді

.

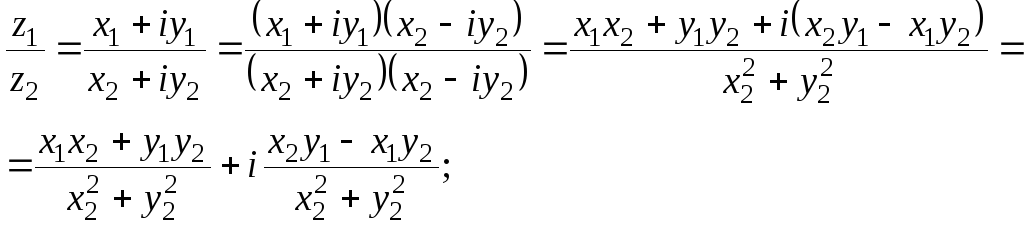
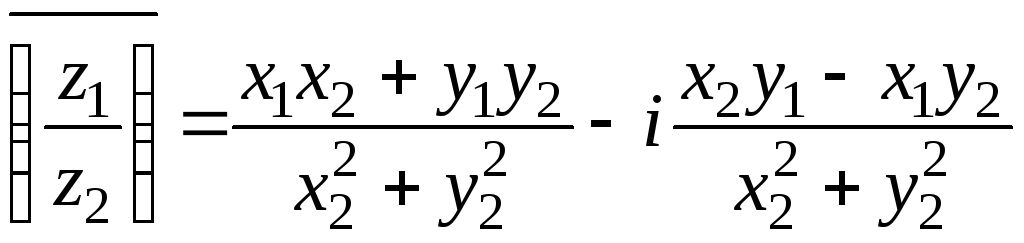Знайдемо

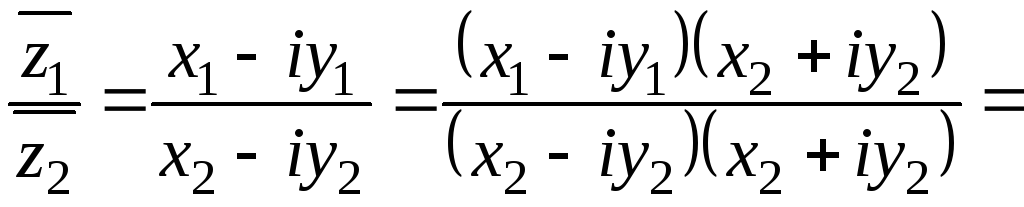
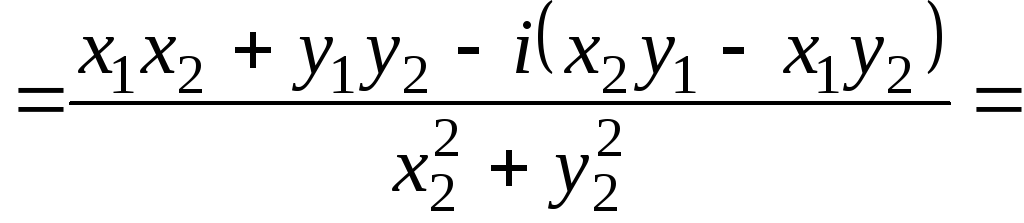
отже, .

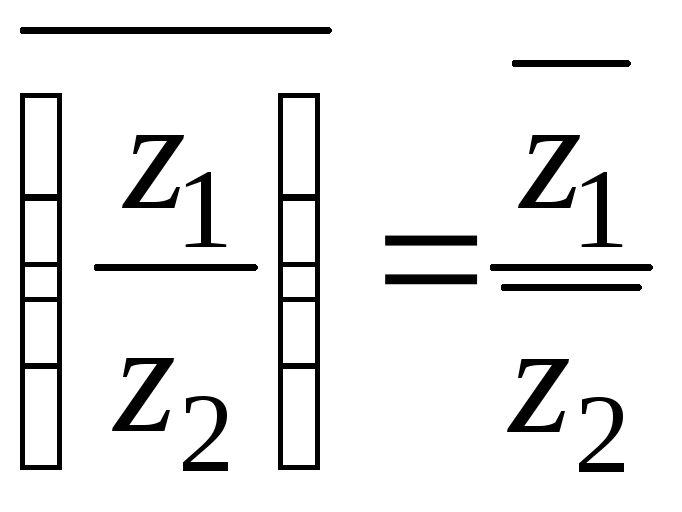4. Нехай , тоді . За визначенням й . Праві частини рівні, отже, .

Приклад 2. Дані комплексні числа запишіть у тригонометричній і показниковій формах:

1) ; 2) ; 3) ; 4) ; 5) ; 6) .

Розв'язок. 1) . Для даного числа ,, .

.

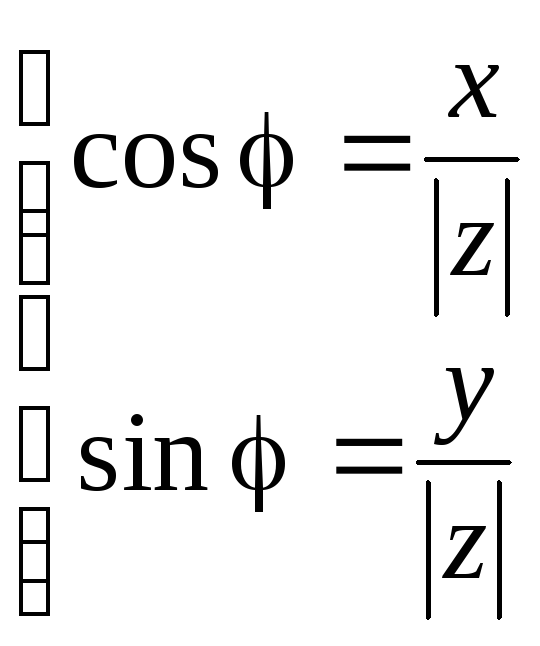
Таким чином, число в тригонометричній формі має вигляд , або ж у показниковій формі .

2) , , . .

Тобто або ж .

3) , . Тоді , ;

.

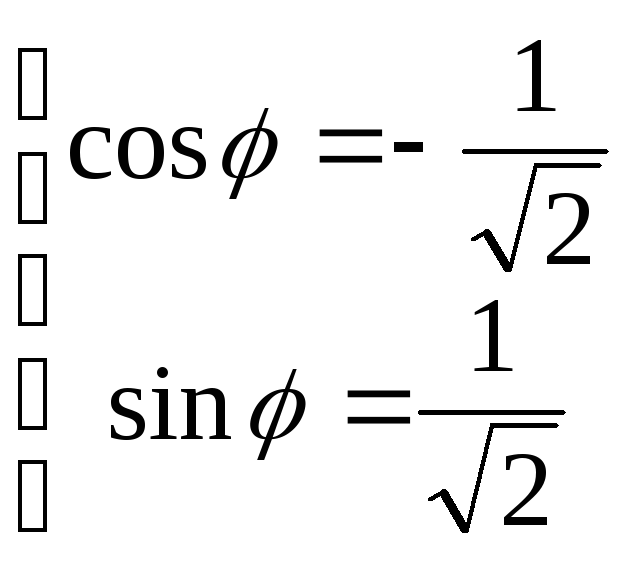
4) , . Тоді , ;

.

5) . Розглянемо чисельник і знаменник окремо. Позначимо через і через . Тоді й . Визначимо й .

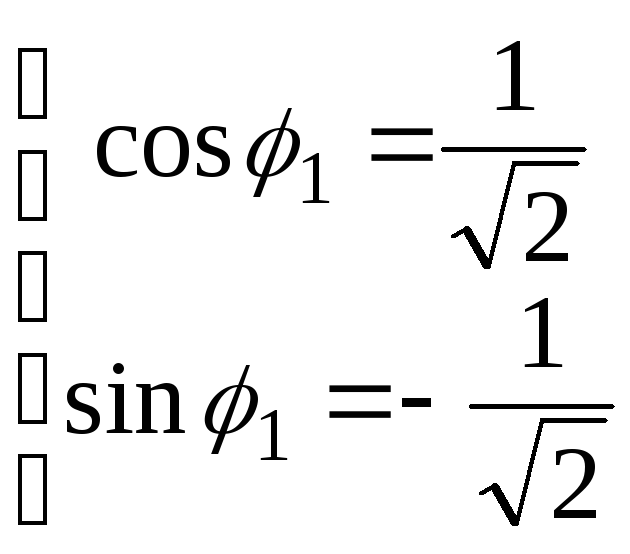
та .

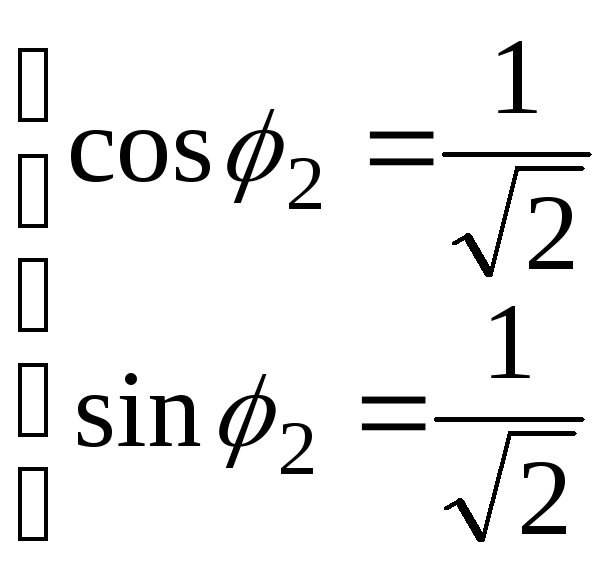
Обчислюємо .

6) ,    , , Визначимо аргумент :

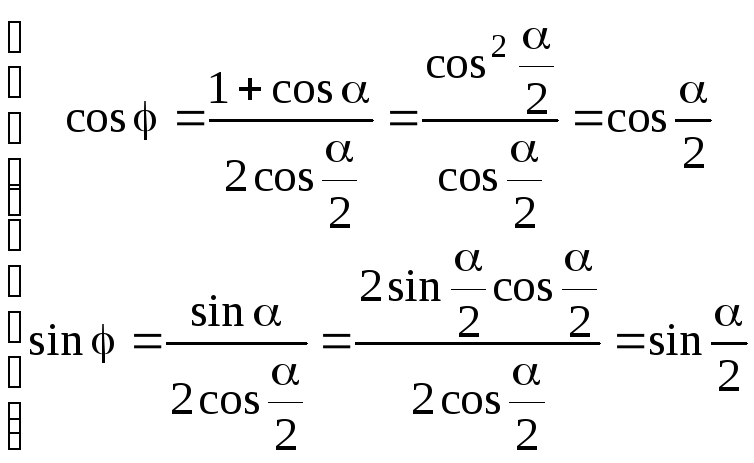
. Тоді

.

Приклад 3. Вкажіть на площині множину точок, які зображують комплексні числа й задовольняють нерівностям:

1) ;

2) ; ;

3) ;

4) .

Розв'язок.

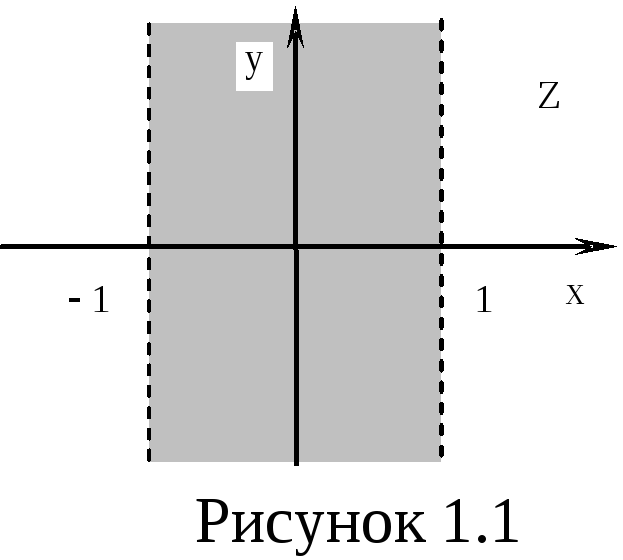
1) – множина точок площини, що лежать між прямими та (рис. 1.1).

2) ; .

Системі нерівностей задовольняють точки комплексної площини, розташовані між прямими , , і (рис. 1.2).

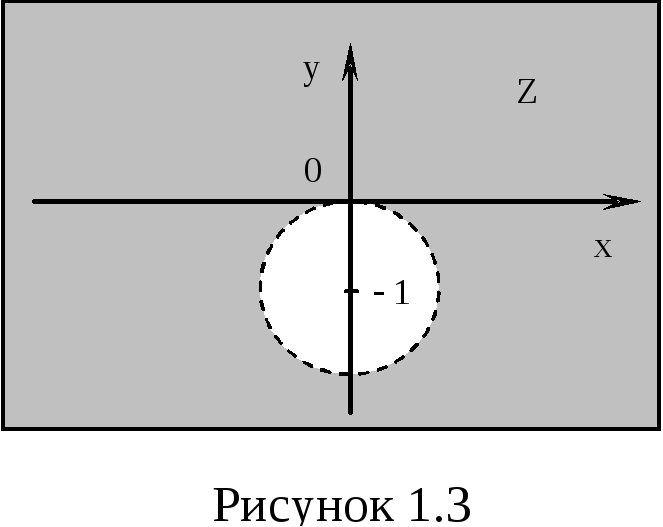
3) . Нехай, тоді. Тоді нерівністьможна переписати у вигляді, або. Таким чином,– множина точок комплексної площини, що лежать поза колом радіусаіз центром у точці(рис. 1.3).

4) . Запишемо нерівність у вигляді, або. Розкривши модуль, одержуємо,

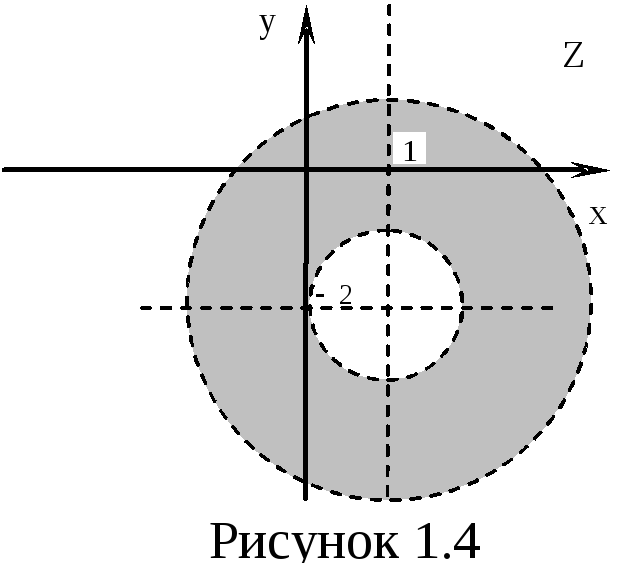
. Нерівності задовольняють точки площини, що лежать між колами радіусів ііз центром у точці(рис. 1.4).

Приклад 4. Обчисліть .

Розв’язок. Якщо , то . Розглянемо . Знайдемо модуль та аргумент цього комплексного числа: , а . Тоді .

Приклад 5. Знайдіть всі значення кореня .

Розв’язок. Використаємо формулу , де

У нашому випадку , . Тоді ,

; при .

; при .

; при .

; при .