Методичні вказівки до практичних занять з дисципліни «Телекомунікаційні та інформаційні мережі» (частина 1) для студентів усіх форм навчання напряму 6.050903 – Телекомунікації / Упоряд.: Ю.М. Бідний, О.М. Буханько. – Харків: ХНУРЕ, 2011. – 64 с.

Упорядники: Ю.М. Бідний,

О.М. Буханько

Рецензент В.В. Ємельянов, професор кафедри МЗ

З МІСТ

Вступ 4

1 Аналіз топологій мереж 5

2 Синтез оптимальних топологій мереж 18

3 Маршрутизація у мережах 38

4 Аналіз потоків у мережах 51

Перелік посилань 60

Додаток А. Варіанти орграфів мереж 61

Додаток Б. Варіанти матриць ваг для графів мереж 63

Додаток в. Варіанти орграфів мереж із заданими величинами потоків та пропускними здатностями дуг 64 вступ

Дисципліна «Телекомунікаційні та інформаційні мережі» (ТтаІМ) належить до нормативних професійно-орієнтованих дисциплін підготовки бакалаврів за напрямом 6.050903 «Телекомунікації» і має на меті одержання студентами знань, вмінь і навичок у галузі аналізу, моделювання і проектування телекомунікаційних та інформаційних мереж.

Метою проведення практичних занять з першої частини дисципліни ТтаІМ є закріплення теоретичного матеріалу, що вивчений на лекціях та під час самостійної роботи, набуття студентами навичок розв’язання практичних задач аналізу і синтезу топологій мереж, маршрутизації та аналізу потоків у мережах.

У результаті проведення практичних занять з 1-ї частини дисципліни ТтаІМ студенти мають знати:

– математичні моделі топологій мереж у вигляді графів і матриць;

– методи та алгоритми синтезу оптимальних згідно з обраним критерієм топологій мереж;

– методи та алгоритми децентралізованої та централізованої маршрутизації у мережах;

– методи та алгоритми аналізу двополюсних і багатополюсних мереж.

Кожне практичне заняття розраховане на 2 години. Під час підготовки до нього студенти мають повторити теоретичний матеріал за конспектом лекцій, рекомендованою літературою і наведеними у методичних вказівках основними теоретичними відомостями, підготувати відповіді на контрольні запитання, розглянути приклади розв’язання задач.

Усі практичні заняття оцінюються викладачем відповідно до якості виконання поставленого завдання і відповіді на контрольні запитання. Отримані при цьому результати істотно впливають на одержання сумарної оцінки у балах за кредитно-модульною системою з дисципліни ТтаІМ. На кожному з практичних занять студент може отримати максимум 5 балів, з яких 1 бал – за присутність, від 2-х до 4-х балів залежно від якості виконання поставленого завдання і відповіді на контрольні запитання.

1 Аналіз топологій мереж

1.1 Мета заняття

Закріплення знань опису та аналізу мережних топологій у вигляді графів і матриць; набуття практичних навичок розв’язання відповідних задач.

1.2 Організація самостійної роботи студентів

1.2.1 Повторіть методи аналізу мережних топологій на основі графів і матриць за конспектом лекцій, літературою [1–4] і наведеними нижче основними теоретичними відомостями.

1.2.2 Дайте відповіді на контрольні запитання.

1.2.3 Розгляньте приклади розв’язання задач.

1.2.4 Розв’яжіть завдання.

1.3 Основні теоретичні відомості

Топологія мережі являє собою схему взаємного розташування кінцевих і вузлових пунктів, а також мережних каналів, яка шляхом указання напрямків і ліній зв'язку визначає потенційні можливості передачі та розподілу інформації між окремими її складовими. Таким чином, для опису та аналізу топології будь-якої мережі потрібно не тільки перелічити фізичні елементи, що входять до її складу, але й вказати можливі види їх зв'язків і взаємодій. З цією метою може бути використано графо-матричний апарат дискретної математики.

Граф мережі можна розглядати як сукупність множини вершин , що відповідають мережним пунктам, і множини ребер , що відповідають мережним лініям (каналам) зв'язку. У випадку симплексних ліній (дуг) граф мережі є орієнтованим графом (орграфом) , у випадку дуплексних – ненаправленим графом, а в інших випадках – змішаним. Ребро (дуга) = графа може розглядатися як лінія, що з'єднує вершини та , і як упорядкована пара цих вершин .

Мережну топологію також можна описати за допомогою матриць. Графові та матричні моделі взаємно доповнюють одна одну у тому розумінні, що можна переходити від одних форм опису топології мережі до інших. Це необхідно, наприклад, при використанні комп'ютерних засобів для опису та аналізу мережних топологій. Розглянемо основні поняття і визначення, які використовуються при цьому.

Одним з таких понять є інцидентність, що характеризує відношення між елементами різнойменних множин та . Наприклад, вершина і дуга орграфа є інцидентними, якщо вершина є для дуги кінцевою вершиною.

Для орграфа напівступенем виходу вершини називається кількість дуг , що виходять з неї; напівступенем заходу вершини – кількість дуг , які заходять до неї; а для неорієнтованого графа ступенем (рангом) вершини – кількість ребер , що інцидентні їй.

Поняття інцидентність формалізується матрицею інцидентності розміром , кожному -му рядку якої відповідає вершина , а кожному -му стовпцю – дуга .

Для орграфа її елемент , , :

– дорівнює +1, якщо дуга виходить з вершини ;

– дорівнює -1, якщо дуга заходить у вершину ;

– дорівнює 0 у всіх інших випадках.

Для неорієнтованого графа:

– дорівнює 1, якщо ребро інцидентне вершині ;

– дорівнює 0 у всіх інших випадках.

Інше поняття – «суміжність» – характеризує відношення між елементами однойменних множин або . Різні вершини називаються суміжними, якщо вони з'єднані дугою (ребром). Різні дуги (ребра) називаються суміжними, якщо вони мають спільну кінцеву вершину.

Поняття «суміжність» формалізується матрицею суміжності розміром , елемент якої , , :

– дорівнює 1, якщо є ребро (дуга) ;

– дорівнює 0 у всіх інших випадках.

Якщо всі ребра графа ненаправлені, то матриця суміжності буде симетричною відносно головної діагоналі, а якщо є направлені ребра (дуги) – несиметричною.

Оскільки елементи матриці суміжності можуть приймати тільки два значення (1 або 0), то вона є булевою матрицею і при операціях з нею використовується апарат булевої алгебри (алгебри логіки).

При розгляді підмножин вершин і ребер (дуг) вихідного графа виникають два поняття: підграф і частковий граф. Підграф містить підмножину вершин ( ) вихідного графа і підмножину його ребер (дуг) ( ), а частковий граф – всі вершини ( ) вихідного графа і підмножину його ребер (дуг) ( ).

Розглянуті складові частини графа дозволяють представити ряд нових понять, якими оперують під час аналізу топології мереж. Одним із таких понять є спрямований шлях на орграфі між парою вершин та . Він є його підграфом, що визначається початковою вершиною , яка є інцидентною одній дузі, що виходить з неї, кінцевою вершиною з єдиною дугою, що заходить до неї, і послідовністю інших дуг, в яких кінець кожної попередньої є початком наступної. Така послідовність може бути описана перерахуванням вершин або дуг.

При вершинному заданні спрямованого шляху перша вершина послідовності називається його початковою вершиною, а остання – кінцевою. Якщо початкова і кінцева вершини спрямованого шляху збігаються, такий шлях називається контуром.

Дане визначення шляху не виключає такі шляхи, в яких вершини або дуги повторюються. Спрямований шлях називається простим, якщо в його вершинному зображенні жодна з вершин не зустрічається більше одного разу. Контур називається простим, якщо він утворений з простого шляху.

Рангом спрямованого шляху називається кількість дуг, що входять до нього. Мінімальний ранг шляху має значення 1, а максимальний – значення (шлях проходить через всі вершини).

Рух по вершинах і ребрах може виконуватися і для неорієнтованих графів. У них аналогом спрямованого шляху є неспрямований шлях (ланцюг) як послідовність вершин і ребер, аналогом контуру – цикл.

Контур (цикл), що з'єднує всі вершини графа, має назву гамільтонового.

Вершина називається досяжною з вершини , якщо існує спрямований шлях із вершини у вершину . Вершина називається контрдосяжною з вершини , якщо існує спрямований шлях із вершини у вершину .

Граф називається зв'язним, якщо будь-які дві його вершини з'єднані, принаймні, одним шляхом (ланцюгом). Орграфи можуть мати також властивість сильної зв’язності. Орграф називається сильно зв'язаним, якщо будь-які дві вершини графа та з'єднані принаймні одним спрямованим шляхом з початком у вершині , і принаймні одним спрямованим шляхом із початком у вершині .

У зв'язних графах будь-які дві вершини можуть бути з'єднані більш ніж одним шляхом (ланцюгом). Під час вирішення ряду завдань доводиться враховувати всі можливі шляхи (ланцюги) з множини , які зв'язують будь-які дві вершини та . У таких завданнях важливою є властивість -зв’язності графа. Граф називається -зв'язним, якщо будь-які дві його вершини з'єднані принаймні шляхами (ланцюгами), що не мають однакових дуг (ребер). Сильно -зв'язним орграфом називається такий, будь-які дві вершини та якого з'єднані принаймні направленими шляхами з початком у вершині , що не мають загальних дуг, і принаймні спрямованими шляхами з початком у вершині , що не мають спільних дуг.

Дві вершини та називаються взаємодосяжними, якщо кожна з них стосовно іншої є і досяжною і контрдосяжною. Оскільки відношення взаємо-досяжності має властивості рефлексивності, симетричності та транзитивності, воно є еквівалентністю. Таким чином, відношення взаємодосяжності розбиває всю множину вершин графа на класи еквівалентності – класи взаємодосяжних вершин. Кожен такий клас породжує підграф, що має назву максимального сильно зв'язного підграфа для графа або компоненти.

Інший підграф, виключення якого із заданого графа призводить до того, що деякі дві вершини та виявляються у різних компонентах, називається перерізом , а його рангом – кількість ребер (дуг), що входять до нього.

Поняття досяжності, контрдосяжності та взаємодосяжності формалізуються за допомогою відповідних топологічних матриць.

Елемент , , матриці досяжності визначається за правилом:

– дорівнює 1, якщо вершина досяжна з вершини ;

– дорівнює 0 у всіх інших випадках.

Елемент , , матриці контрдосяжності визначається за правилом:

– дорівнює 1, якщо вершина контрдосяжна з вершини ;

– дорівнює 0 у всіх інших випадках.

З визначення матриць і маємо справедливість рівності для будь-яких відповідних елементів матриць, що, у свою чергу, обумовлює такі дві рівності: , . Тут – матриця, транспонована до матриці , – матриця, транспонована до матриці .

Елемент матриці взаємодосяжності визначається за правилом

, , . (1.1)

Топологічні булеві матриці суміжності, досяжності, контрдосяжності та взаємодосяжності дають лише загальне уявлення про можливі шляхи та перерізи у графі мережі. Для їхнього конкретного визначення використовується інша булева матриця – структурна розміром , в якій елемент , , визначається за правилом:

– дорівнює 1, якщо = ;

– дорівнює , якщо є ребро (дуга) , ;

– дорівнює , якщо є ребро (дуга) , ;

– дорівнює 0, якщо такого ребра (дуги) немає.

Структурна матриця є матрицею прямих зв'язків, елементи якої являють собою множину шляхів рангу між кожною парою вершин графа мережі. Тому вона також має назву матриці зв'язності. При зведенні її до другого ступеня ( ) елементи визначають множину шляхів рангу між всіма парами вершин графа. Оскільки для графа з вершинами максимальний ранг шляхів , то, визначивши матрицю , можна одержати всі шляхи, які існують між всіма парами вершин графа.

Матрицю необов'язково зводити до максимального ступеня , якщо при її зведенні до деякого ступеня виявиться, що . Це означає, що вже визначено всі можливі шляхи між парами вершин графа мережі. Матриця називається характеристичною або матрицею всіх можливих шляхів.

Зі структурної матриці також можна знайти множину всіх шляхів від вершини витоку до вершини стоку (отримувача) за рахунок розкриття визначника підматриці , яка отримана зі структурної матриці викреслюванням рядка, що відповідає вершині , і стовпця, що відповідає вершині :

.

Обчислення визначників виконується розкладанням їх за входженнями якого-небудь рядка або стовпця, що дає можливість при кожній операції знизити порядок визначника на одиницю.

Розкладання визначника матриці рангу з елементами по -му рядку буде мати вигляд

,

де – визначник матриці доповнення, отриманої з матриці викреслюванням -го рядка та -го стовпця.

Для визначників третього і другого порядку можна застосувати звичайну процедуру розкриття по діагоналі, вважаючи .

Графічним еквівалентом методу визначення множини всіх шляхів від вершини-витоку до інших вершин-стоків є побудова дерева шляхів, яке будується по структурній матриці у такий спосіб:

1. Вершина-витік позначається через і обирається -й рядок матриці .

2. По цьому рядку вибираються номери вершин , для яких , і утворюється множина вузлів, що мають від вершини шлях рангу 1 (вершини першого ярусу).

3. Вершини -го ярусу зі шляхами рангу від цих вершин знаходяться почерговим переглядом рядків вершин із номерами у ( -1)-му ярусі, які не зустрічалися на шляху від вершини до вершини .

4. Побудова дерева шляхів триває або до отримання шляхів максимально припустимого рангу, або доти, поки для вершини не виявиться, що всі вершини вже ввійшли до шляху .

Якщо отриману множину шляхів записати у булевій формі (як диз'юнкцію кон’юнкцій символів ребер (дуг), причому кожен додаток відповідає кожному зі шляхів розглянутої множини), то множина перерізів між вершиною і вершиною визначається за правилом, яке засноване на знаходженні двоїстої булевої функції:

– всі знаки диз'юнкції змінюються знаками кон’юнкції та навпаки;

– всі дужки розкриваються відповідно до законів булевої алгебри.

Кожен додаток отриманого виразу буде представляти один із можливих перерізів їх множини .

1.4 Приклади розв’язання задач

Задача 1. Для графа мережі (рис. 1.1) знайти напівступені виходу, заходу і рангів його вершин, а також топологічні матриці суміжності, досяжності, контрдосяжності та взаємодосяжності.

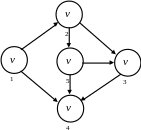
Рисунок 1.1 – Орграф мережі

Розв’язання

З наведених у п. 1.3 понять маємо: для вершини напівступінь виходу , напівступінь заходу ; для вершини напівступінь виходу , напівступінь заходу ; для вершини напівступінь виходу , напівступінь заходу ; для вершини напівступінь виходу , напівступінь заходу ; для вершини напівступінь виходу , напівступінь заходу .

Поняття ступінь (ранг) вершини має сенс тільки для неорієнтованого графа. Тому при заміні в орграфі мережі (рис. 1.1) дуг неспрямованими ребрами маємо: для вершини ступінь (ранг) ; для вершини ступінь (ранг) ; для вершини ступінь (ранг) ; для вершини ступінь (ранг) ; для вершини ступінь (ранг) .

Знайдемо топологічну матрицю суміжності та матрицю досяжності орграфа мережі за їх визначенням (п. 1.3):

, .

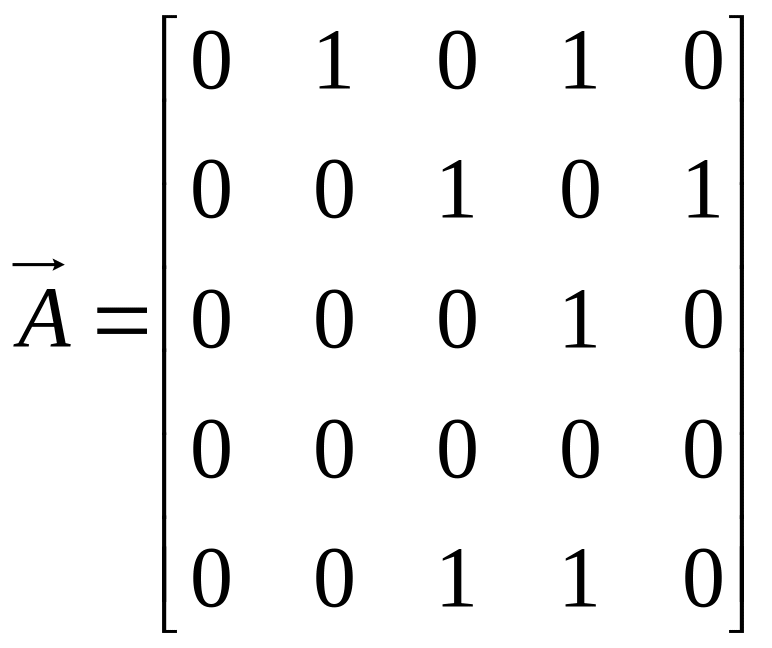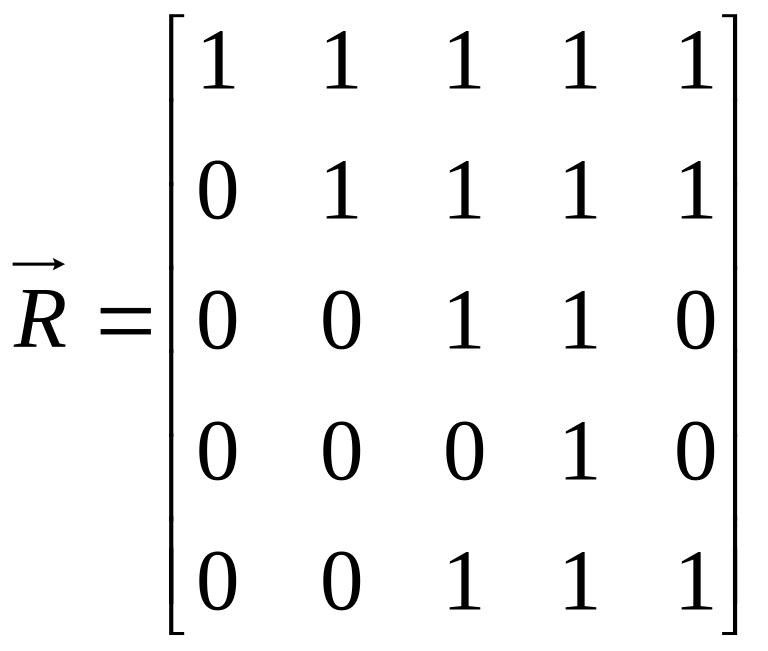Матрицю контрдосяжності знаходимо шляхом транспонування матриці досяжності ( ), а матриця взаємодосяжності – відповідно (1.1):

, .

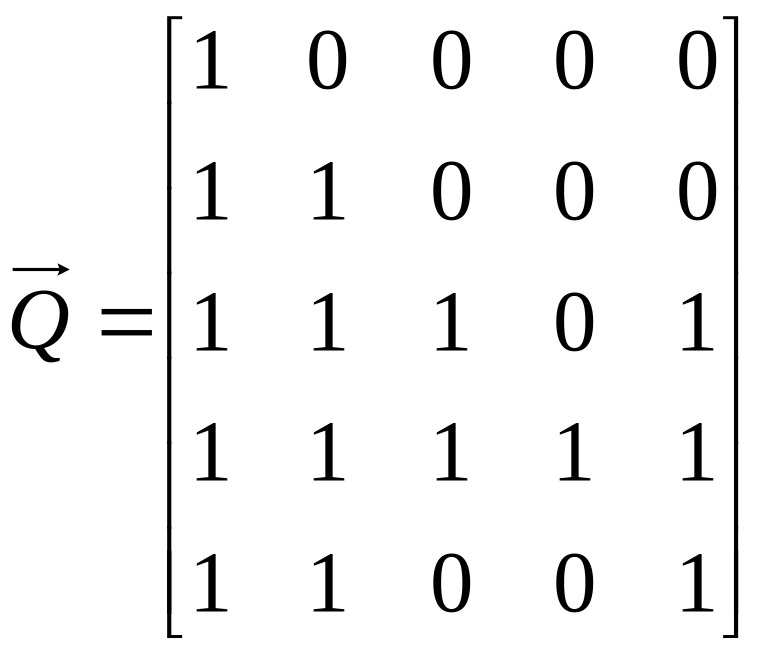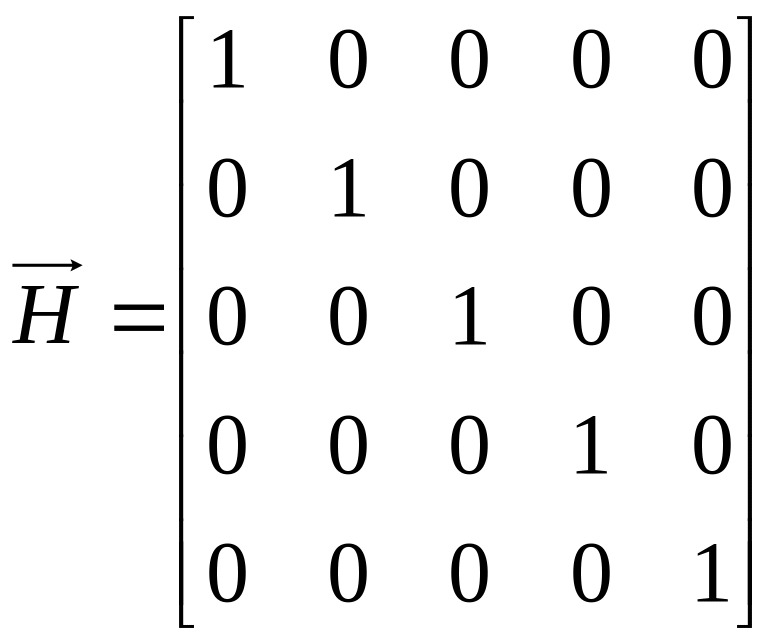Задача 2. Розкласти орграф мережі (рис. 1.2) на максимально сильно зв'язні підграфи (компоненти).

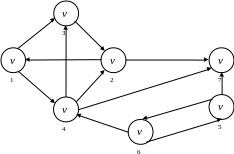
Рисунок 1.2 – Орграф мережі

Розв’язання

Знайдемо графічним методом матрицю досяжності та матрицю контрдосяжності :

, .

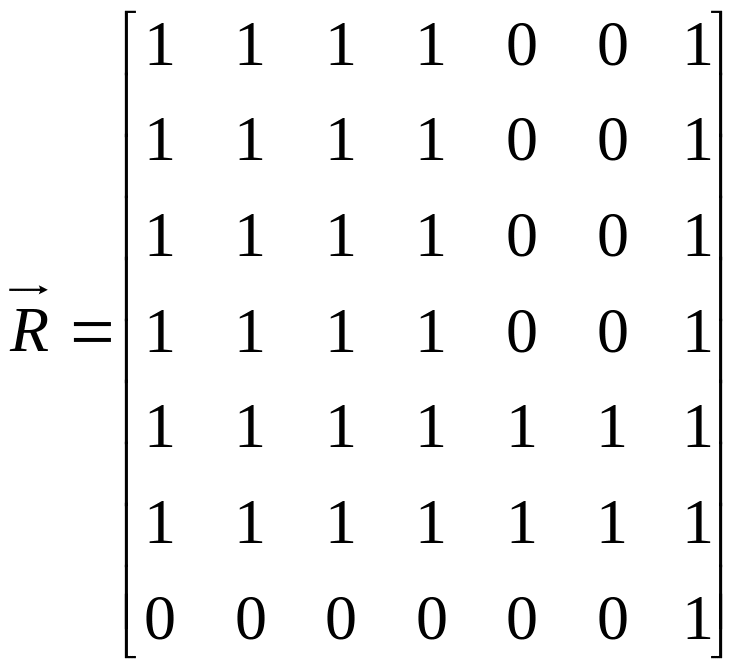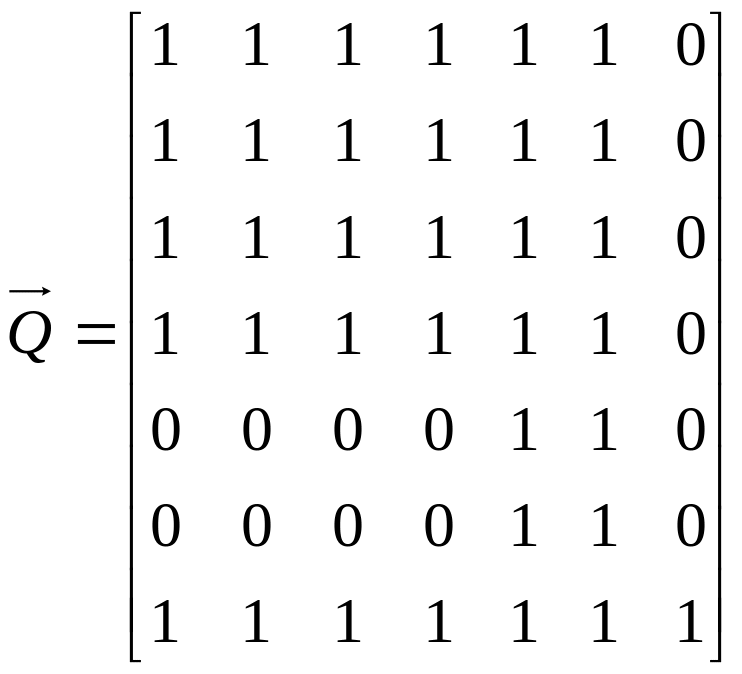Відповідно до (1.1) матриця взаємодосяжності має вигляд

.

Аналізуючи матрицю , знаходимо такі класи взаємодосяжних вершин орграфа мережі: , , .

Задача 3. Для змішаного графа мережі (рис. 1.3) знайти структурну матрицю і множину шляхів між всіма парами вершин.

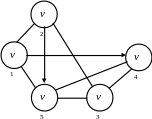
Рисунок 1.3 – Змішаний граф мережі

Розв’язання

Введемо позначення для ребер (дуг) змішаного графа мережі (рис. 1.3): , , , , , , , .

Знайдемо структурну матрицю за її визначенням (п. 1.3):

.

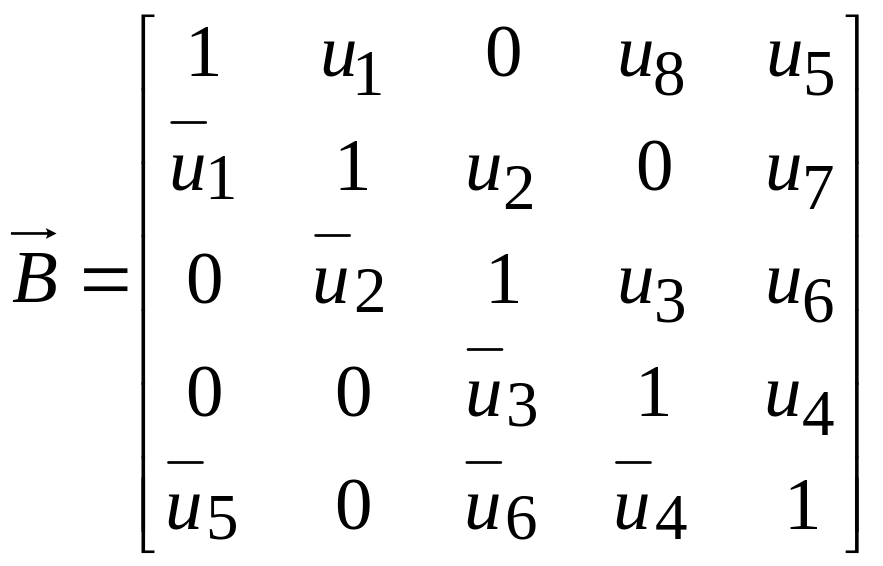Покажемо процес одержання матриці . Для отримання елемента варто використати елементи першого рядка і другого стовпця матриці :

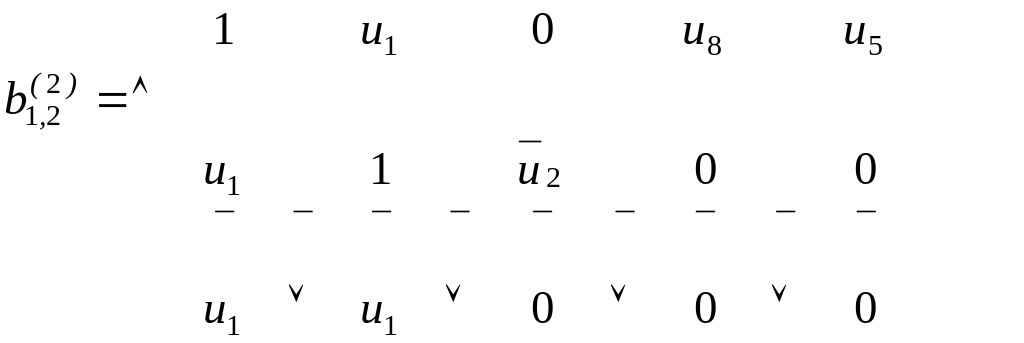
Аналогічно отримуємо інші елементи матриці :

, . , , , , і т.д.

Отримані результати зведемо у матрицю :

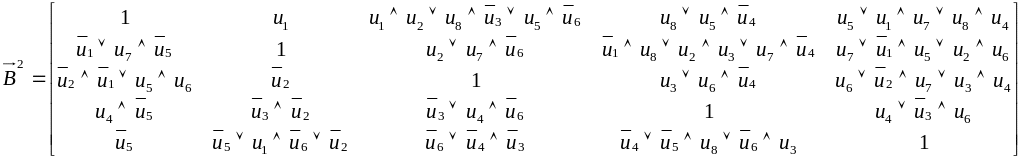
З порівняння матриць і видно, що отримана матриця не є характеристичною, тому що , і процес обчислень варто продовжити, зокрема:

– обчислити ;

– якщо , то і результат отриманий;

– якщо , то продовжити обчислення, тобто знайти .

Оскільки =4 для даного графа мережі, матриця буде характеристичною.

У характеристичній структурній матриці кожен елемент , тобто визначає множину всіх шляхів із вершини до вершини .

Наприклад,

.

Задача 4. Для змішаного графа мережі (рис. 1.3) побудувати дерево шляхів із вершини-витоку до всіх інших вершин-стоків.

Розв’язання

Вершина-витік є коренем дерева і розміщується на нульовому ярусі ( ). На першому ярусі ( ) розміщуються вершини , , , які мають безпосередній зв'язок із вершиною . На другому ярусі ( ) від вершини розташовуються вершини і , які безпосередньо зв'язані з нею. Вершину виключаємо з розгляду, оскільки шлях у вершину вже пройшов через вершину . Від вершини на другому ярусі ( ) розміщуються вершини і , а від вершини – вершини і . Аналогічно записуються вершини на інших ярусах дерева. Побудоване дерево шляхів із вершини-витоку до всіх інших вершин-стоків показано на рис. 1.4.

Рисунок 1.4 – Дерево шляхів з вершини-витоку

Задача 5. Для змішаного графа мережі (рис. 1.5) знайти множину шляхів та їхніх перерізів у випадку вершини-витоку і вершини-стоку .

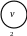
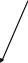
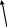
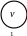
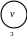
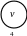
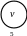
Рисунок 1.5 – Змішаний граф мережі

Розв’язання

Введемо позначення для ребер (дуг) графа мережі (рис. 1.5): , , , , , , , .

Знайдемо структурну матрицю з її визначення (п. 1.3):

.

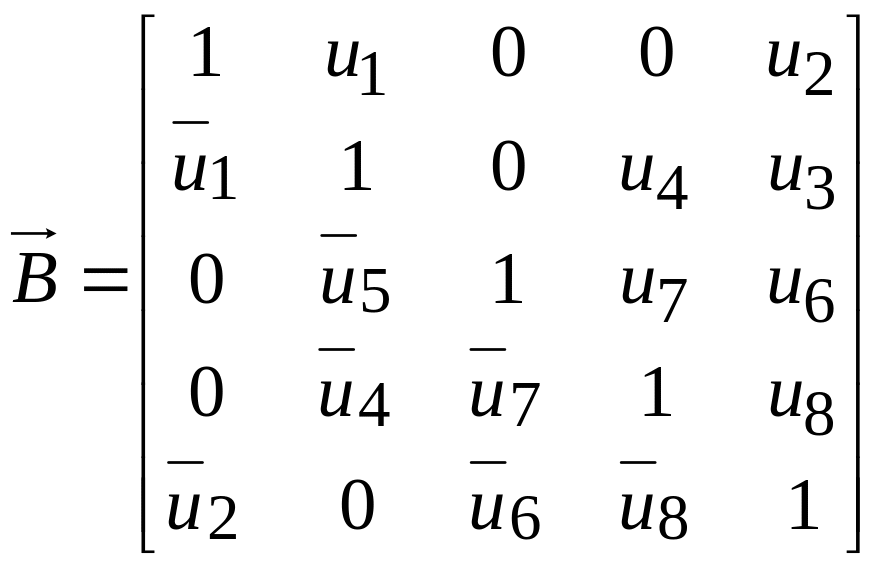Розглянемо визначення множини шляхів від вершини-витоку до вершини-стоку за матрицею відповідно до (п. 1.3):

.

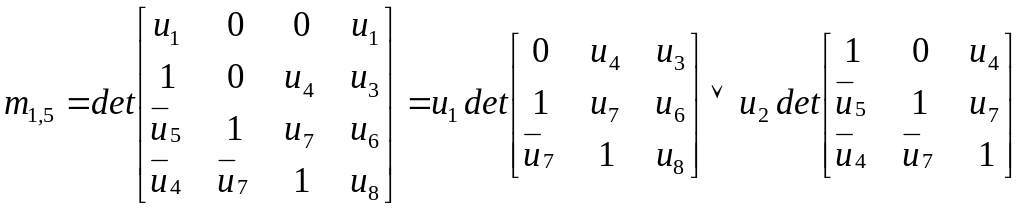Перший з отриманих визначників розкладаємо за діагоналями, а другий дорівнює одиниці (див. п. 1.3). У результаті одержимо множину шляхів із вершини-витоку до вершини-стоку :

.

Для знаходження множини перерізів обчислюємо двоїсту булеву функцію:

1.5 Контрольні запитання

1. Що являє собою топологія мережі?

2. У чому суть графічного подання мережної топології?

3. Які види графів використовуються для опису мережних топологій?

4. Що являє собою матрична модель мережної топології?

5. Що означає поняття інцидентності для графа мережі?

6. Як визначається матриця інцидентності для мережної топології?

7. Що являє собою напівступінь виходу вершини, напівступінь заходу вершини та ступінь (ранг) вершини для графа мережі?

8. Що означає поняття «суміжність» для графа мережі?

9. Як визначається матриця суміжності для мережної топології?

10. Які складові частини топології мережі називаються підграфом і частковим графом?

11. Що означають поняття «направлений шлях» або «ланцюг» для графа мережі?

12. Що являє собою ранг шляху?

13. Що означають поняття «контур» або «цикл» для графа мережі?

14. Які графи мереж називаються зв'язними, сильно зв'язними, -зв'язними, сильно -зв'язними?

15. Що означають поняття «досяжність», «контрдосяжність» і «взаємодосяжність» вершин графа мережі?

16. Що означає поняття «компоненти графа мережі»?

17. Що означає поняття «переріз графа мережі»?

18. Що являє собою ранг перерізу?

19. Як визначаються матриці досяжності, контрдосяжності і взаємодосяж-ності для мережної топології?

20. Як визначається структурна матриця для мережної топології?

21. Як визначити множини шляхів між всіма парами вершин графа мережі?

22. Як визначити множину шляхів між заданою парою вершин графа мережі?

23. Як визначити множину перерізів між заданою парою вершин графа мережі?

1.6 Завдання для самостійного розв’язання

1 Знайдіть топологічні матриці інцидентності, суміжності, досяжності, контрдосяжності, взаємодосяжності та структурну для заданого викладачем варіанта орграфа мережі (додаток А).

2 Розв’яжіть завдання 1 у випадку неорієнтованого графа мережі.

3 Знайдіть множину шляхів та їхніх перерізів для заданої викладачем пари вершин орграфа мережі в умовах завдання задачі 1.

4 Розв’яжіть задачу 3 у випадку неорієнтованого графа мережі.