3.4 Приклади розв’язання задач

Задача 1. Знайти з використовуючи алгоритм Беллмана–Форда, найкоротші шляхи від вершини-витоку до інших вершин графа мережі на рис. 3.1.

Рисунок 3.1 – Зважений граф мережі

Розв’язання

Застосуємо алгоритм Беллмана–Форда (п. 3.3.1):

=1 (рис. 3.2, а):

;

.

=2 (рис. 3.2, б):

;

.

=3 (рис. 3.2, в):

;

;

.

=4 (рис. 3.2, в):

.

а б в

Рисунок 3.2 – Дерева найкоротших -шляхів для послідовності кроків алгоритму Беллмана–Форда: а) =1; б) =2; в) =3, 4

Задача 2. Знайти, використовуючи алгоритм Дейкстри, найкоротші шляхи від вершини-витоку до інших вершин орграфа мережі на рис. 3.3.

Рисунок 3.3 – Зважений орграф мережі

Розв’язання

Застосуємо алгоритм Дейкстри (п. 3.3.2):

Крок 1. , для всіх .

Крок 2. .

Крок 3.

,

,

,

,

.

Крок 4. «Позначаємо» вершину та дугу .

Крок 5. .

Крок 6. Визначаємо, що не всі вершини «позначені».

Крок 3.

,

,

,

.

Крок 4. «Позначаємо» вершину та дугу .

Крок 5. .

Крок 6. Визначаємо, що не всі вершини «позначені».

Крок 3.

,

,

.

Крок 4. «Позначаємо» вершину та дугу .

Крок 5. .

Крок 6. Визначаємо, що не всі вершини «позначені».

Крок 3.

,

.

Крок 4. «Позначаємо» вершину та дугу .

Крок 5. .

Крок 6. Визначаємо, що не всі вершини «позначені».

Крок 3.

Крок 4. «Позначаємо» вершину та дугу .

Крок 5. .

Крок 6. Визначаємо, що всі вершини «позначені».

«Позначені» вершини й дуги утворять орієнтоване дерево найкоротших шляхів, яке наведено на рис. 3.4.

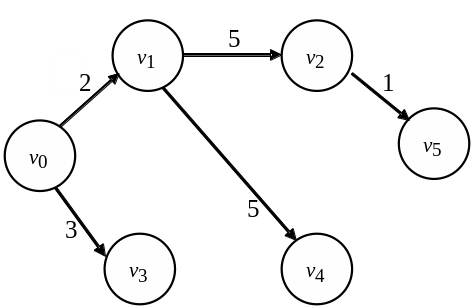
Рисунок 3.4 – Дерево найкоротших шляхів від вершини-витоку до інших вершин вихідного графа мережі

Задача 3. Знайти, використовуючи алгоритм Флойда, дистанційну та маршрутну матриці для визначення найкоротших шляхів між всіма парами вершин змішаного графа мережі на рис. 3.5

Рисунок 3.5 – Зважений граф мережі

Розв’язання

Для заданого графа запишемо початкові значення дистанційної й маршрутної матриць (п. 3.3.3).

, .

Ітерація 1. Вершину визначимо як базову, тому у матриці виключаємо перший рядок і перший стовпець. Оскільки у базовому рядку в стовпцях 3, 5, 6, 7 і 8 знаходяться елементи, які мають значення , то елементи цих стовпців можна не досліджувати. У базовому першому стовпці у рядках 3, 5, 6, 7 і 8 також знаходяться елементи, які мають значення , і елементи цих рядків можна не досліджувати. Для того, щоб визначити, чи призведе використання вершини 1 до появи більш коротких шляхів, ніж записані у матриці , необхідно досліджувати за допомогою тримісної операції (3.3) лише елементи , . Застосування операції (3.3) дає такі результати:

;

.

Оскільки =12< = і =12< = , зазначені елементи заносимо у матрицю , а інші елементи матриці переносимо у без змін. Елементи матриці при цьому: та , тому що .

, .

Виконуючи аналогічні обчислення на ітераціях 2, 3, 4, 5, 6, 7 і 8, одержимо результуючі матриці й . Рішення, отримане на ітерації 5, не поліпшується на наступних ітераціях. Отже, оптимальне рішення: , .

, .

Задача 4. Визначити положення центрального вузла мережі як медіани її графа на рис. 3.6.

Рисунок 3.6 – Зважений граф мережі

Розв’язання

Використовуючи алгоритм Флойда (п. 3.3.3), знайдемо мінімальні шляхи між всіма парами вершин графа мережі та запишемо результат у вигляді дистанційної матриці шляхів :

Визначимо внутрішні передаточні числа для вершин графа:

,

,

,

,

.

Найменшим є число , отже, вершина є внутрішньою медіаною графа.

Визначимо зовнішні передаточні числа для вершин графа:

,

,

,

,

.

Найменшим є число , отже, вершина є зовнішньою медіаною графа.

Для визначення медіани знаходимо . Отже, медіаною графа є вершина .