2.3.2 Топологія мережі у вигляді найкоротшого гамільтонова циклу

Найкоротший гамільтонів цикл графа мережі , як його частковий граф, являє собою ненаправлений шлях із мінімальною сумою ваг , що проходить через усі вершини графа таким чином, що початкова і кінцева вершини збігаються.

Задача синтезу найкоротшого гамільтонова циклу також має назву «замкнутої задачі комівояжера», який, виїжджаючи з деякого пункту, має побувати у кожному з інших пунктів рівно один раз і повернутися у вихідний пункт, проїхавши найменшу сумарну відстань.

Для розв’язання цієї оптимізаційної задачі можна використовувати алгоритм Літтла, що реалізує метод гілок і границь. Вихідними даними у ньому є довжини ребер графа між його вершинами, що утворять матрицю порядку , елемент якої дорівнює вазі ребра між -ю та -ю вершинами, а при відсутності останнього або при йому надається нескінченне значення. Маршрут подається як множина упорядкованих пар вершин: , кожна з якої є його ланкою. Довжина маршруту дорівнює сумі відповідних цим ланкам елементів матриці відстаней: . Очевидно, що для будь-якого припустимого маршруту кожен рядок і кожен стовпець матриці містять рівно по одному елементу, що відповідає цьому маршруту. Тому для побудови оптимального (мінімального) маршруту необхідно вибрати рівно один мінімальний елемент у кожному рядку і кожному стовпці матриці .

Основними процедурами алгоритму Літтла є обчислення нижніх границь довжин маршрутів, визначення субоптимальних рішень і розходження з метою одержання нових (більш коротких) маршрутів, що дозволяє в кінцевому рахунку визначити оптимальний маршрут. Розглянемо докладніше ці процедури.

Для обчислення нижньої границі довжини поточного маршруту на кожному -му кроці роботи алгоритму використовується поняття редукції поточної матриці відстаней, що полягає у наступному. Якщо з кожного елемента деякого рядка поточної матриці відстаней відняти постійну величину , то довжина будь-якого маршруту, обумовлена новою матрицею, менша за довжину того ж маршруту, обумовлену старою матрицею, на величину . Це твердження справедливе тому, що кожному маршруту відповідає рівно один елемент даного рядка. Однак відносні довжини всіх маршрутів залишаться незмінними. Отже, при переході від вихідної матриці відстаней до нової залишаться незмінними і всі оптимальні маршрути. Очевидно, що аналогічне твердження справедливе і для елементів стовпців матриці відстаней, якщо з кожного елемента певного стовпця матриці відстаней відняти постійну величину .

Якщо – довжина маршруту , обумовлена поточною матрицею відстаней до виконання редукції, – довжина того ж маршруту, обумовлена скороченою матрицею і

(2.1)

– сума всіх констант, які використовуються під час обчислення скороченої матриці , то

. (2.2)

Оскільки скорочена матриця відстаней містить тільки ненегативні елементи, то є нижньою границею довжини маршруту для нескороченої поточної матриці відстаней.

Для виділення субоптимальних рішень по скороченій матриці відстаней доцільно обрати ланку нульової довжини, а потім послідовно додавати ланки нульової чи мінімальної довжини. Ця процедура заснована на двох базових твердженнях. По-перше, якщо обирається ланка , то рішення не має містити інших ланок, що відповідають елементам -го рядка або -го стовпця. По-друге, якщо ланку можна виключити з остаточного рішення, то її можна не розглядати під час виконання наступних обчислень. Отже, для кожної ланки досить розглянути такі два випадки. У першому з них ланка включається у поточне (субоптимальне) і всі наступні (субоптимальні) рішення, поки визначається маршрут. У другому випадку ланка виключається з подальшого розгляду.

Процес розбивання множини всіх маршрутів на непересічні підмножини може бути подано у вигляді розгалуження дерева, як показано на рис. 2.3. Вузол з позначкою «Всі маршрути» відповідає множині всіх маршрутів. Вузол із позначкою відповідає множині, що містить ланку . Вузол із позначкою відповідає підмножині «Всі маршрути», які не містять ланку . На рис. 2.3 подальше розгалуження з вузла не вказується. Вузол із позначкою відповідає всім маршрутам, що містять обидві ланки і . Як і раніше, вузол із позначкою відповідає всім маршрутам, що містять ланку , але не утримуючої ланки .

Всі маршрути

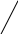
Рисунок 2.3 – Процес розгалуження при побудові підмножин

Мету розгалуження можна пояснити у такий спосіб: якщо здійснюється розбивання множини всіх маршрутів на все більш дрібні підмножини, то зрештою буде отримана підмножина, що містить один єдиний маршрут. Ланки або пари вершин, що утворять цей маршрут, можуть бути відновлені, якщо рухатися по дереву у зворотному напрямку, тобто до початкового вузла (з позначкою «Всі маршрути»). Процес розгалуження здійснюється на основі порівняння нижніх границь. Якщо на якомусь -му кроці алгоритму нижня границя довжин маршрутів з однієї підмножини перевищує нижню границю, що відповідає іншій підмножині, то першу підмножину можна виключити з розгляду на наступному ( )-му кроці. Іншими словами, розгалуження з відповідного вузла не виробляється.

Припустимо, що з деякого вузла дерева рішень виходять дві гілки, та розглянемо кінцеві вузли цих гілок. Тоді вузол, що відповідає підмножині маршрутів, які містять нову ланку, позначатимемо через , а вузол, що відповідає підмножині маршрутів, які не містять нової ланки, позначатимемо через .

Мета розгалуження полягає у розбивці множини маршрутів на дві таких підмножини та , що найкращий маршрут із найбільш ймовірно міститься в і найменш ймовірно – в . Як відзначалося вище, у першу чергу у підмножину мають включатися маршрути, що містять ланки , для яких елементи скороченої матриці дорівнюють нулю. Однак у кожному рядку і кожному стовпці цієї матриці може міститися не один нульовий елемент. Питання полягає у тому, яку з відповідних їм ланок варто включити у підмножину . Для того, щоб відповісти на дане запитання, розглядаються маршрути, що можуть бути включені у підмножину , тобто маршрути, що не містять ланку . Оскільки вершина має бути зв'язана з деякою іншою вершиною, то кожен маршрут із підмножини має містити ланку, довжина якої не менше мінімального елемента -го рядка скороченої матриці , не враховуючи елемента, що відповідає ланці . Відповідну відстань позначимо через . Оскільки необхідно, щоб у вершину можна було б потрапити з будь-якої іншої вершини, то кожен маршрут із підмножини містить ланку, довжина якої не менше мінімального елемента -го стовпця скороченої матриці , не вважаючи елемента, що відповідає ланці . Позначимо цю відстань через , а суму величин і – через . Величини називаються вторинними штрафами. Якщо ланка не включається у можливий маршрут, то ланка, що відповідає деякому іншому елементу -го рядка скороченої матриці , і ланка, що відповідає деякому іншому елементу її -го стовпця, мають входити в остаточний маршрут. Величина дорівнює мінімальному штрафу, якщо не включати ланки в оптимальний маршрут. Якщо цей штраф обчислити для всіх ланок, яким відповідають нульові елементи скороченої матриці , то можна порівняти відповідні значення і включити у поточний маршрут ланку , за невикористання якої платився б максимальний штраф. Очевидно, що вибір ланки , яка відповідає максимальному штрафу, дозволяє визначити нову підмножину маршрутів, що не містять цієї ланки. Нижня границя для відповідної йому гілки дерева має бути обрана таким чином, щоб вона не перевищувала довжини жодного з маршрутів, що не містять ланки . Дана вимога буде виконана, якщо нову нижню границю покласти рівній сумі попередньої нижньої границі і максимального штрафу за невикористання ланки :

,

при чому для визначення досліджуються всі нульові елементи скороченої матриці . Слід зазначити, що для всіх ланок , яким відповідають ненульові елементи скороченої матриці .

Перед тим, як визначити нову нижню границю для підмножини маршрутів, що містять ланку , необхідно здійснити перетворення скороченої матриці . Відзначимо, що якщо у маршрути включається ланка , то надалі можна не розглядати -й рядок і -й стовпець цієї матриці. Далі, якщо ланка вже належить певному маршруту з підмножини , то ланка на наступних кроках не може належати маршруту з . Виконання даної умови можна досягти, дорівнюючи елемент поточної матриці ваг, що відповідає ланці на всіх наступних кроках алгоритму. Крім того, можуть існувати інші ланки, за допомогою яких надалі також можуть бути утворені підмаршрути – цикли, що включають в себе неповні множини вершин вихідного графа . Ці ланки називаються забороненими. Їх можна виключити з розгляду, прирівнюючи елементи матриці , що відповідають вагам цих ланок, також рівним .

Після проведеного перетворення скороченої матриці виникає нова поточна (для ( )-го кроку) матриця ваг , з якою знову виконується процедура редукції та обчислюється нове значення . Нижня границя для підмножини при цьому може бути тепер обчислена у вигляді

.

Виконуючи аналогічні обчислення для , розгалуження має здійснюватися з вузлів із найменшою нижньою границею. Побудований у результаті повний маршрут є оптимальним, якщо його довжина не перевищує довжини будь-якого маршруту, який відповідає іншим ланкам дерева. Щоб виключити всі маршрути, що містять ланку , відповідне значення оберненого елемента матриці приймається рівним .

2.3.3 Комірчаста топологія мережі у вигляді М-структури

Рішення задачі синтезу багатозв’язної комірчастої топології мережі (М-структури) з мінімальною сумою ваг ребер графа містить такі етапи.

Етап 1. На множині всіх вершин графа мережі будується найкоротше дерево G' за алгоритмами Краскала або Прима. Отриманий у результаті частковий граф G' є однозв'язним. У той же час для забезпечення надійності доставки інформації потрібно, щоб топологія мережі була як мінімум двозв’язною і не містила «висячих» вершин. Здійснено перехід до етапу 2.

Етап 2. Визначається множина всіх «висячих» вершин часткового графа G', що утворюють його підграф G». Для них будується найкоротший гамільтонів ланцюг або найкоротший гамільтонів цикл. У результаті об'єднання найкоротшого дерева і найкоротшого гамільтонова ланцюга або найкоротшого гамільтонова циклу формується М-структура, для якої виконується умова багатозв’язності.

2.4 Приклади розв’язання задач

Задача 1. Синтезувати з використанням алгоритму Краскала найкоротше дерево (НКД) для зваженого графа мережі (рис. 2.4).

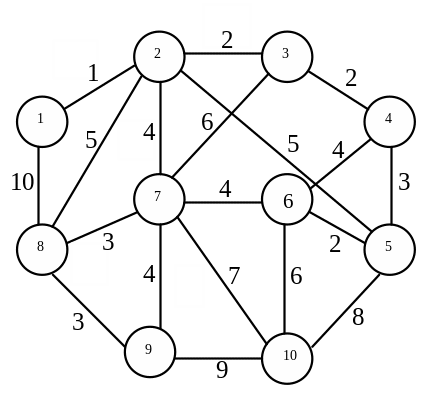
Рисунок 2.4 – Зважений граф мережі

Розв’язання

Для зваженого графа мережі (рис. 2.4) запишемо список ребер графа мережі у вигляді табл. 2.1.

Таблиця 2.1 – Список ребер зваженого графа мережі

Вага ребра	Ребра	Примітка
1	(1, 2)	Включаємо у НКД ребро (1, 2)
2	(2, 3), (3, 4), (5, 6)	Включаємо у НКД ребра (2, 3), (3, 4), (5, 6)
3	(4, 5), (7, 8), (8, 9)	Включаємо у НКД ребра (4, 5), (7, 8), (8, 9)
4	(2, 7), (4, 6), (6, 7), (7, 9)	Включаємо у НКД ребро (2, 7), а ребра (4, 6), (6, 7), (7,9) призводять до утворення циклів, тому їх не включаємо в НКД
5	(2, 8), (2, 5)	Ребра (2, 8), (2, 5) призводять до утворення циклів, тому їх не включаємо в НКД
6	(3, 7), (6, 10)	Включаємо у НКД ребро (6, 10), а ребро (3, 7) призводить до утворення циклу, тому його не включаємо у НКД
7	(7, 10)	Не включаємо у НКД, тому що воно вже побудоване
8	(5, 10)	Не включаємо у НКД, тому що воно вже побудоване
9	(9, 10)	Не включаємо у НКД, тому що воно вже побудоване
10	(2, 8)	Не включаємо у НКД, тому що воно вже побудоване

В икористовуючи табл. 2.1, побудуємо найкоротше дерево (рис. 2.5).

Рисунок 2.5 – Найкоротше дерево для зваженого графа мережі

Задача 2. Синтезувати з використанням алгоритму Прима найкоротше дерево зваженого графа мережі для заданої у вигляді табл. 2.2 матриці ваг його ребер (каналів зв’язку).

Таблиця 2.2 – Матриця ваг ребер графа мережі

	1	2	3	4	5	6	7	8	9	10
1	0	5,5	5,4	8,6	12,7	12,7	11.1	13,4	12,1	19,8
2	5,5	0	7,0	8,0	8,9	7,3	6,4	11,7	11,8	16,7
3	5,4	7,0	0	3,6	9,6	12,6	13,3	8,5	6,7	15,5
4	8,6	8,0	3,6	0	6,8	11,5	13,7	4,9	3,8	12,0
5	12,7	8,9	9,6	6,8	0	7,3	11,8	5,5	8,3	8,0
6	12,7	7,3	12,6	11,5	7,3	0	5,5	12,5	14,4	14,2
7	11,1	6,4	13,3	13,7	11.8	5,5	0	16,3	17,4	19,3
8	13,4	11,7	8,5	4,9	5,5	12,5	16,3	0	3,5	7,4
9	12,1	11,8	6,7	3,8	8,3	14,4	17,4	3,5	0	10,6
10	19,8	16,7	15,5	12,0	8,0	14,2	19,3	7,4	10,6	0

Розв’язання

Відповідно до алгоритму Прима спочатку виписуємо перший рядок матриці без першого стовпця, що відповідає організації зв'язку від першої вершини до інших -х ( ):

2	3	4	5	6	7	8	9	10
5,5	5,4	8,6	12,7	12,7	11.1	13,4	12,1	19,8

Вибираємо у цьому рядку мінімальний елемент . Далі викреслюємо 3-й стовпець матриці , що відповідає йому, і, рухаючись по 3-ому рядку, порівнюємо значення наведених у ньому елементів з їх значеннями в першому рядку без першого і 3-го стовпців. Якщо значення елемента 3-го рядка у відповідному стовпці виявляється меншим за значення, зазначене у першому рядку, то ці значення міняються місцями. Якщо найменшим буде значення у першому рядку, то заміна не виконується. Таким чином, формується наступний рядок:

2	4	5	6	7	8	9	10
5,5	3,6 (3)	9,6 (3)	12,6 (3)	11.1	8,5 (3)	6,7 (3)	15,5 (3)

При цьому цифрою 3 у дужках позначено ті значення ваг, що взяті з третього рядка.

Знову вибираємо мінімальний елемент рядка . Діючи аналогічно до попереднього, одержуємо новий рядок:

2	5	6	7	8	9	10
5,5	6,8 (4)	11,5 (4)	11,1	4,9 (4)	3,8 (4)	12,0 (4)

Вибираємо мінімальний елемент рядка .

Нижче показано подальший процес пошуку.

2	5	6	7	8	10
5,5	6,8 (4)	11,5 (4)	11,1	3,5 (9)	10,6 (9)

2	5	6	7	10
5,5	5,5 (8)	11,5 (4)	11,1	7,4 (8)

5	6	7	10
5,5 (8)	7,3 (2)	6,4 (2)	7,4 (8)

6	7	10
7,3 (2)	6,4 (2)	7,4 (8)

6	10
5,5 (7)	7,4 (8)

10

7,4 (8)

Таким чином, найкоротше дерево (НКД) (рис. 2.6) міститиме ребра довжиною , , , , , , і загальною довжиною 46,6 одиниць.

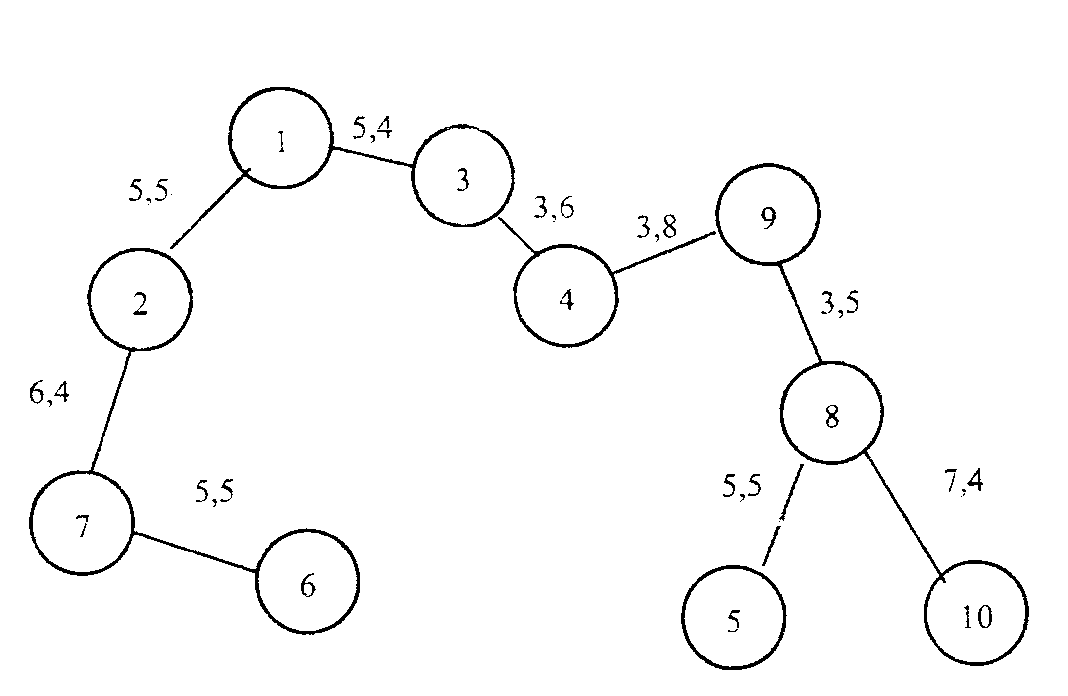
Рисунок 2.6 – Найкоротше дерево за алгоритмом Прима для задачі 2

Задача 3. Синтезувати найкоротше дерево графа мережі в умовах задачі 1 з додатковими вершинами у точках Штейнера (транзитними вузлами).

Розв’язання

Скористаємося результатами розв’язання задачі 2 з використанням алгоритму Прима (рис. 2.6). З рис. 2.7 видно, що є чотири умовних трикутники: 123, 276, 489, 5810 (рис. 2.7).

А2

А3

А1

А4

Рисунок 2.7 – Найкоротше дерево з транзитними вузлами у точках Штейнера

Використовуючи наведені вище правила, побудуємо НКД із точками Штейнера. З елементарної математики відомо, що довжина медіани на сторону дорівнює:

.

Величина кутів проти сторони :

 ,

проти сторони :

 ,

проти сторони :

 ,

де – радіус описаної окружності:

,

– напівпериметр умовного трикутника:

.

Виконавши відповідні обчислення, знаходимо, що для даного графа мережі з десятьма вершинами можна побудувати найкоротше дерево з введенням чотирьох додаткових транзитних вузлів у точках Штейнера . При цьому загальна вага топології мережі складе 42,8 одиниць, тобто скоротиться на 8 % у порівнянні з розв’язанням задачі 2. Якщо таке скорочення «ваги» топології мережі економічно вигідне, отримане рішення буде доцільним.

Задача 4. Синтезувати з використанням алгоритму Літтла найкоротший гамільтонів цикл для графа мережі на рис. 2.8.

Рисунок 2.8 – Вихідний зважений граф мережі

Розв’язання

Матриця ваг для графа на рис. 2.8 має вид, показаний нижче. Вона є поточною матрицею відстаней для 1-го кроку алгоритму Літтла: .

.

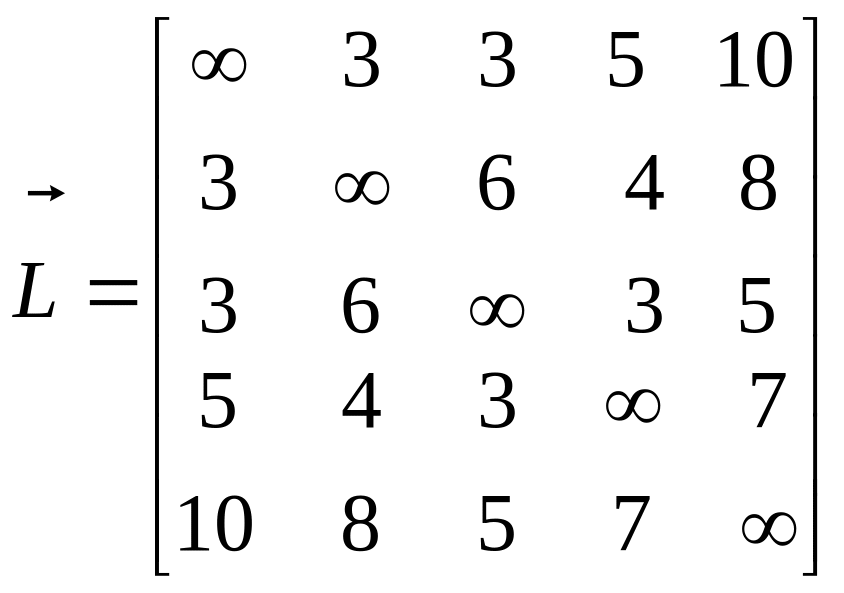1-й крок. Виконуємо спочатку редукцію рядків поточної матриці ваг . Для цього у кожному рядку визначаємо мінімальний елемент і знайдене значення віднімаємо з елементів відповідного рядка. Результати виконання редукції рядків у вигляді матриці наведено нижче, де додатковий вектор-стовпець містить від'ємники-константи при редукції.

.

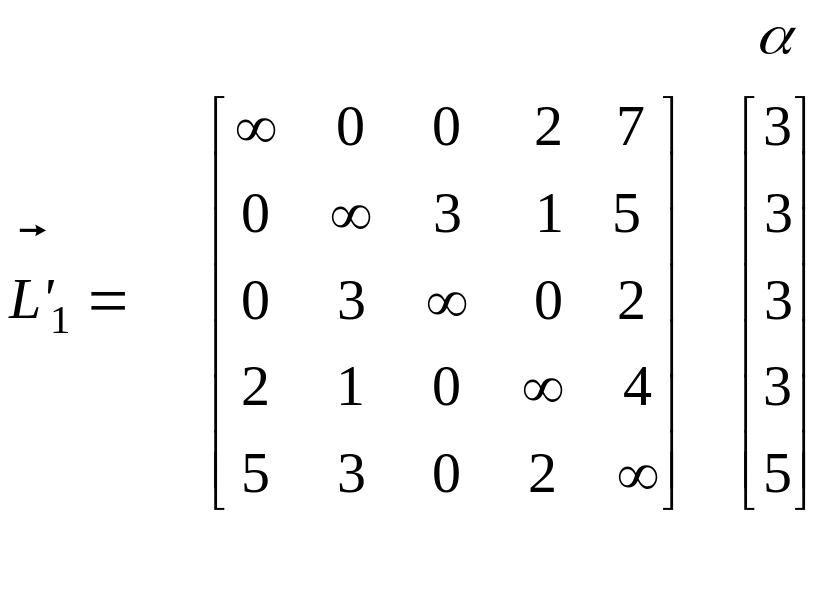Потім виконуємо редукцію стовпців, результати якої у вигляді матриці наведено нижче, де додатковий вектор-рядок містить від'ємники-константи при редукції. Значення елемента, розташованого на перетині вектора-стовпця і вектора-рядка , дорівнює сумі всіх констант, що віднімаються =19. Це значення є нижньою границею довжин всіх маршрутів на даному кроці: =19.

.

На рис. 2.9 зображено початковий вузол дерева, що відповідає множині всіх маршрутів, і зазначено нижню границю довжин всіх маршрутів.

19

Всі маршрути

Рисунок 2.9 – Початковий вузол дерева рішень

За скороченою матрицею відстаней далі визначаємо мінімальні ненульові значення її рядків і стовпців, які записуємо відповідно у вигляді вектора-стовпця і вектора-рядка . Матриця разом із цими векторами показана нижче.

.

Відповідні елементам векторів і значення вторинних штрафів для різних ланок (пар вершин) з нульовими значеннями ваг для них наведені у табл. 2.3.

Таблиця 2.3 – Вторинні штрафи на 1-му кроці алгоритму Літтла

	3
	5
	4
	5

Як видно з табл. 2.3, максимальне значення дорівнює 5. Вибираючи ланку , можна одержати виграш у відстані, рівний 5, що більше, ніж при виборі будь-якої іншої ланки, за винятком ланки . Отже, як базову ланку на 1-му кроці розгалуження вибирають ланку , а , . Нижньою границею довжин маршрутів із підмножини на наступному (2-му кроці) є величина .

Отже, модифікована матриця відстаней після викреслювання 1-го рядка і 3-го стовпця, а також заміни елемента на перетин 3-го рядка і 1-го стовпця матриці на має вигляд:

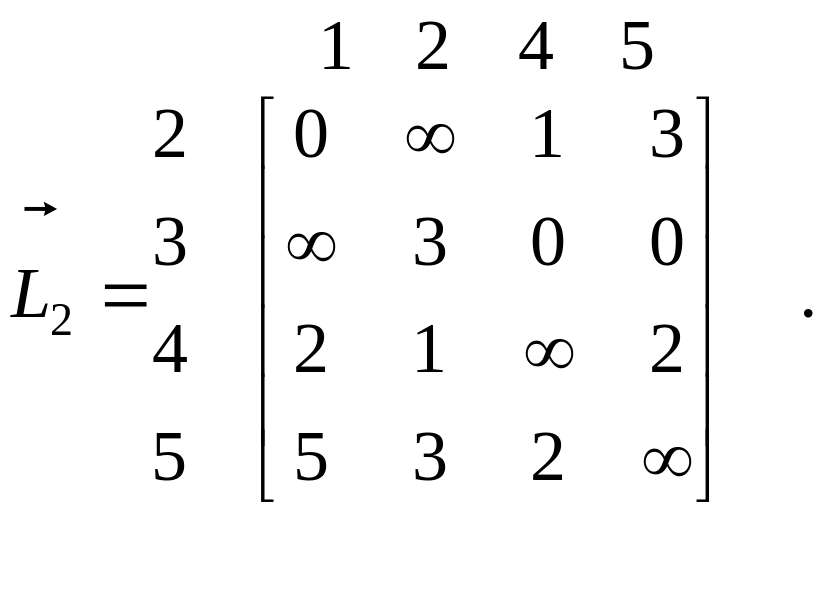
2-й крок. Виконуємо спочатку редукцію рядків поточної матриці відстаней. Для цього у кожному рядку визначаємо мінімальний елемент і знайдене значення віднімаємо з елементів відповідного рядка. Результати виконання редукції рядків у вигляді матриці наведено нижче, де додатковий вектор-стовпець містить від'ємники-константи при редукції.

.

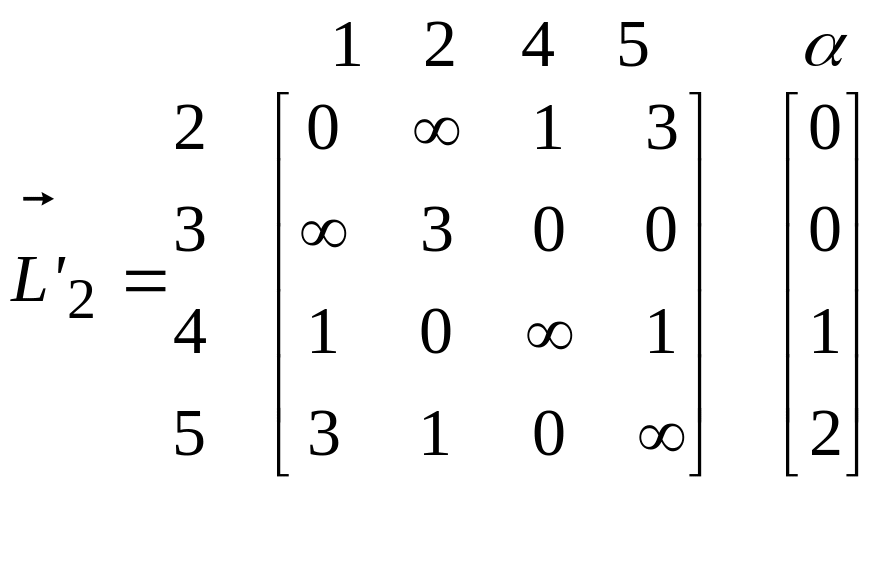Потім виконуємо редукцію стовпців, результати якої у вигляді матриці наведено нижче, де додатковий вектор-рядок містить від'ємники-константи при редукції. Значення елемента, розташованого на перетині вектора-стовпця і вектора-рядка , дорівнює сумі всіх констант, що віднімаються: =3. Це значення дозволяє визначити нову нижню границю довжин всіх маршрутів на даному кроці: =22.

.

Дерево рішень тепер може бути зображене так, як це показано на рис. 2.10.

19

Всі маршрути

24

22

Рисунок 2.10 – Дерево рішень на 2-му кроці алгоритму Літтла

За скороченою матрицею ваг далі визначаємо мінімальні ненульові значення її рядків і стовпців, які записуємо відповідно у вигляді вектора-стовпця і вектора-рядка . Матриця разом з цими векторами показана нижче.

.

Відповідні елементам векторів і значення вторинних штрафів для різних ланок (пар вершин) з нульовими значеннями ваг для них наведено у табл. 2.4.

Як видно з табл. 2.4, максимальне значення дорівнює 4. Вибираючи ланку , можна одержати виграш у вазі, рівний 4, що більше, ніж при виборі будь-якої іншої ланки, за винятком ланки . Отже, як базову ланку на 2-му кроці розгалуження вибираємо ланку , а , . Нижньою границею довжин маршрутів із підмножини на наступному (3-му кроці) є величина =26.

Таблиця 2.4 – Вторинні штрафи на 2-му кроці алгоритму Літтла

	2
	4
	4
	2
	2

Модифікована матриця відстаней після викреслювання 3-го рядка і 5-го стовпця має вигляд:

.

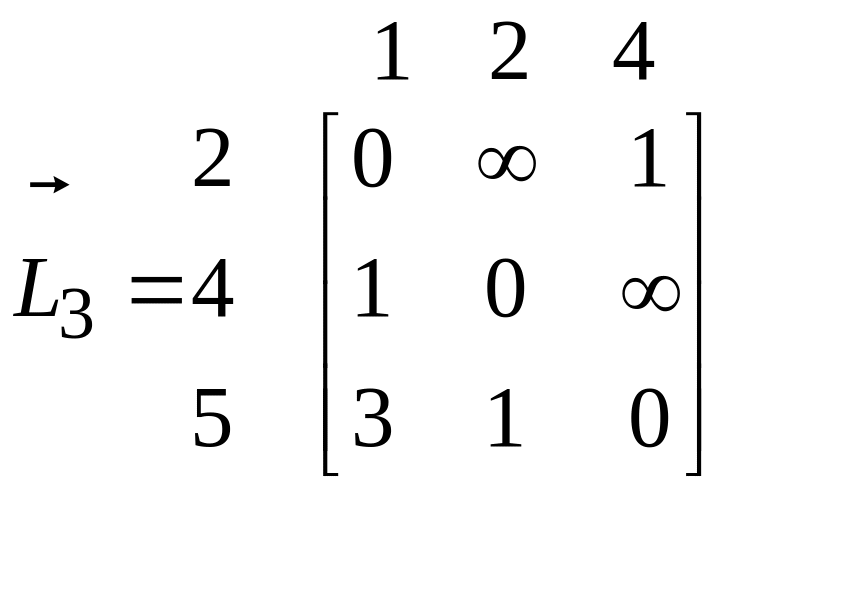Після завершення алгоритму кінцеве дерево рішень на 5-му кроці може бути зображене так, як показано на рис. 2.11.

Всі маршрути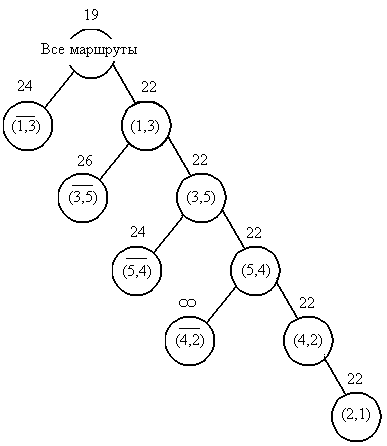

Рисунок 2.11 – Дерево рішень на 5-му кроці алгоритму Літтла

Побудований повний маршрут є оптимальним, якщо його довжина не перевищує довжини будь-якого маршруту, який відповідає іншим ланкам дерева, що і має місце у даному прикладі. Він складається з таких ланок чи пар вершин і має сумарну довжину =22. Цей оптимальний маршрут є мінімальним гамільтоновим циклом, який зображено на рис. 2.12.

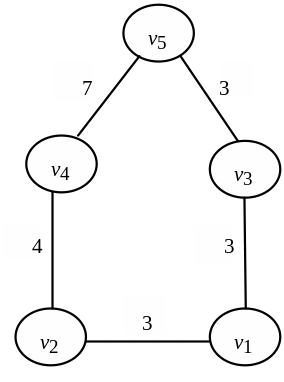
Рисунок 2.12 – Мінімальний гамильтонів цикл графа мережі

2.5 Контрольні запитання

1. Які матриці кількісних характеристик використовуються при синтезі оптимальних відповідно до обраного критерію топологій мереж?

2. У чому полягає завдання синтезу топології мережі у вигляді найкоротшого дерева?

3. Які принципи покладені в основу розв’язання задачі синтезу найкоротшого дерева?

4. Які вихідні дані використовуються при розв’язанні задачі синтезу найкоротшого дерева?

5. Яку послідовність операцій реалізує алгоритм Краскала для синтезу найкоротшого дерева?

6. Яку послідовність операцій реалізує алгоритм Прима для синтезу найкоротшого дерева?

7. Що являють собою точки Штейнера?

8. Які правила використовуються для визначення положення точки Штейнера при трьох основних вершинах графа мережі?

9. Як визначити положення точок Штейнера при чотирьох основних вершинах графа мережі?

10. У чому полягає задача синтезу топології мережі у вигляді найкоротшого гамільтонового циклу (замкнута задача комівояжера)?

11. Які вихідні дані використовуються при розв’язанні задачі синтезу найкоротшого гамільтонового циклу за алгоритмом Літтла?

12. Які процедури використовуються під час розв’язання задачі синтезу найкоротшого гамільтонового циклу за алгоритмом Літтла?

13. Які етапи містить розв’язання задачі синтезу коміркової топології мережі у вигляді М-структури?

2.6 Завдання для самостійного розв’язання

1. Знайдіть за алгоритмами Краскала і Прима найкоротші дерева для заданого викладачем варіанта матриці ваг повнозв’язного графа мережі (додаток Б) і порівняйте отримані при цьому результати.

2. Знайдіть за алгоритмом Літтла найкоротший гамільтонів цикл для графа мережі в умовах завдання 1.

3. Знайдіть комірчасті M-структури для графа мережі в умовах і розв’язаннях завдання 1.