2 Синтез оптимальних топологій мереж

2.1 Мета заняття

Закріплення знання методів та алгоритмів синтезу оптимальних відповідно до обраного критерію мережних топологій; набуття практичних навичок їх використання під час розв’язання відповідних задач.

2.2 Організація самостійної роботи студентів

2.2.1 Повторіть методи та алгоритми синтезу оптимальних відповідно до обраного критерію топологій мереж на основі їх графових і матричних моделей за конспектом лекцій, літературою [1–5] і наведеними нижче основними теоретичними відомостями.

2.2.2 Дайте відповіді на контрольні запитання.

2.2.3 Розгляньте приклади розв’язання задач.

2.2.4 Розв’яжіть завдання.

2.3 Основні теоретичні відомості

При синтезі оптимальних відповідно до обраного критерію базових мережних топологій вони звичайно розглядаються як часткові графи зважених повнозв’язних графів , ребрам яких відповідають деякі кількісні характеристики (ваги) ребер (каналів зв'язку), а графам у цілому – їх матриці ваг (довжин, часу доставки інформації та ін.) розміром , елементи яких , , :

– рівні вазі ребра ;

– рівні при відсутності ребра ;

– рівні 0, якщо вершина = .

Як критерій оптимальності мережної топології при цьому приймається мінімум суми ваг її ребер.

Розглянемо методи та алгоритми синтезу топологій мереж таких типів:

– оптимальної деревоподібної у вигляді найкоротшого дерева;

– оптимальної кільцевої у вигляді найкоротшого гамільтонового циклу;

– оптимальної комірчастої у вигляді М-структури.

2.3.1 Топологія мережі у вигляді найкоротшого дерева

Дерево , як частковий граф повнозв’язного графа мережі , має такі властивості:

– кількість його ребер із множини на одиницю менше кількості вершин з множини ( );

– дерево зв'язне і не має циклів;

– додавання ребра між двома несуміжними вершинами дерева приводить до появи циклу;

– видалення будь-якого ребра дерева призводить до втрати зв’язності;

– будь-які дві вершини дерева з'єднані єдиним ланцюгом.

Дерево з мінімальною сумою ваг його ребер має назву найкоротшого.

Під час розв’язання задачі синтезу такої мережної топології викорис-товуються такі принципи вибору -го ребра графа мережі :

– всяка ізольована вершина графа мережі з'єднується з іншою найближ-чою вершиною;

– всякий ізольований фрагмент графа мережі з'єднується з іншим най-ближчим фрагментом.

Під фрагментом мережі розуміють підмножину вершин її графа, зв'язану прямими ребрами, кожне з яких з'єднує вершини цієї підмножини. Ізольованою є вершина, яка на поточному етапі синтезу топології мережі ще не зв'язана з іншими вершинами (фрагментами). Аналогічно визначається ізольований фрагмент. Найближчим сусідом вершини (фрагмента) є той, який знаходиться від даного на мінімальній відстані.

При синтезі топології мережі у вигляді найкоротшого дерева найбільш широко використовуються алгоритми Краскала і Прима, а також введення додаткових вершин у точках Штейнера.

1. Алгоритм Краскала

При відносно невеликій кількості вершин і ребер для розв’язання задачі синтезу мережної топології у вигляді найкоротшого дерева може застосову-ватися алгоритм Краскала, сутність якого полягає у наступному.

Для графа мережі з вершинами складається список його ребер у порядку збільшення значень їхніх ваг. Потім здійснюється вибір ребер, починаючи з того, яке має мінімальне значення ваги. Якщо чергове обране ребро призводить до утворення циклу, його відкидають. Після вибору ребра процес побудови найкоротшого дерева завершується.

2. Алгоритм Прима

Принцип роботи цього алгоритму полягає у наступному. Вибирається початкова вершина дерева, наприклад , і знаходиться перше ребро цього дерева з-поміж інцидентних вершині із мінімальним значенням ваги . На наступному кроці алгоритму Прима вибирається найкоротше ребро з ребер, інцидентних фрагменту дерева, що утворився на попередньому кроці (у даному випадку інцидентних вершинам і , які не ведуть до утворення циклів). Якщо є декілька таких ребер, може бути обране кожне з них. Процедура повторюється доти, доки не буде обране ребро найкоротшого дерева.

У матричній формі покрокова робота цього алгоритму може бути описана таким чином.

Крок 1. Виписується рядок матриці , що містить елемент із мінімальною вагою, наприклад, , без відповідного йому стовпця, що узгоджується з організацією зв'язку від вершини до всіх інших.

Крок 2. Вибирається у цьому рядку мінімальний елемент, наприклад, .

Крок 3. Викреслюється -й стовпець матриці і, рухаючись по -му рядку цієї матриці, порівнюються значення наведених у ній елементів з їхніми значеннями, наведеними у виписаному рядку цієї матриці без першого і -го стовпців. Якщо значення якого-небудь елемента -го рядка у відповідному стовпці має менше значення, ніж зазначено у виписаному рядку, воно заноситься у рядок із вказівкою того, звідки його взято. У результаті формується новий виписаний рядок.

Кроки 2–3 повторюються доти, доки не буде обране ребро найкоротшого дерева.

3. Найкоротше дерево з додатковими вершинами у точках Штейнера

Сумарну довжину ребер мережної топології у вигляді найкоротшого дерева можна зменшити, якщо ввести додаткові вершини (транзитні вузли) у так званих точках Штейнера.

При трьох вершинах , , графа мережі точка Штейнера буде розташована у місці перетину кіл, описаних навколо рівносторонніх трикутників, які побудовані на двох сторонах вихідного трикутника, як це показано на рис. 2.1.

Рисунок 2.1 – Положення точки Штейнера при трьох вершинах графа мережі

Крім того, у випадку трьох вершин графа мережі можна використовувати такі правила.

1. У гострокутних трикутниках близьким до оптимального є найкоротше дерево з точкою Штейнера , яка розташована на медіані найменшого кута при віддаленні від його протилежної сторони на відстань, що дорівнює довжині цієї сторони, поділеній на .

2. У трикутниках, один із кутів яких більше 90°, але менше 120°, близьким до оптимального є найкоротше дерево з точкою Штейнера , яка розташована на медіані найбільшого кута при віддаленні від його протилежної сторони на відстань, що дорівнює довжині цієї сторони, поділеній на .

3. У трикутниках, один з кутів яких дорівнює 120° або більше, не можна одержати найкоротше дерево, менше суми двох сторін, що утворюють цей кут.

При чотирьох вузлах , , , вводяться дві додаткові точки Штейнера і , що знаходяться на перетині кіл, описаних біля рівносторонніх трикутників, які побудовані на протилежних сторонах вихідного дерева, з лінією, що з'єднує треті вершини цих трикутників (рис. 2.2). У цьому випадку найкоротше дерево з точками Штейнера буде мати сумарну довжину ребер у разів меншу, ніж дерево, яке побудоване на чотирьох вихідних вершинах.

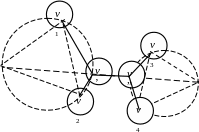
Рисунок 2.2 – Положення точок Штейнера при чотирьох вихідних вершинах графа мережі

Для мереж із кількістю вершин не існує загальних правил визначення положень точок Штейнера при синтезі найкоротшого дерева. Таких точок може бути не більше , і вони визначаються шляхом розбивання множини вершин на її підмножини, що містять 3 або 4 вершини.