13 Кільце лишків. Алгоритм евкліда

13.1 Мета заняття

Ознайомити студентів з основними властивостями подільності у кільці Z; застосувати алгоритм Евкліда для визначення найбільшого загального дільника двох чисел і для лінійного подання НСД; проілюструвати формальні теоретико-кільцеві конструкції на прикладі кілець лишків.

13.2 Методичні вказівки з організації самостійної роботи

За темою студент повинен знати: алгоритм Евкліда; основні властивості подільності [3, c. 176-183; 58-61].

13.3 Контрольні запитання й завдання

1. Сформулюйте Малу теорему Ферма.

2. Чому дорівнює добуток НСД , НСК?

3. Описати алгоритм Евкліда.

13.4 Приклади розв’язання аудиторних задач

Приклад 1.Використовуючи Малу теорему Ферма, знайти остачу від діленняна 7.

Розв’язок. Згідно з Малою теоремою Ферма для будь-якого цілого числа, яке не ділиться на просте, має місце порівняння.

Вважаємо ,.

Тоді . Підводимо вираз у 9-й степінь.

. Тоді

. Остача від ділення на 7 дорівнює 1.

Приклад 2.Використовуючи Малу теорему Ферма, знайти остачу від діленняна 13.

Розв’язок. Вважаємо,.

Тоді . Подамо. Підводимо вираз у 2-й степінь.

. (13.1)

З іншого боку . Підводимо вираз у 3-й степінь.

.

. Число 216 має остачу 8 при діленні на 13.

. (13.2)

Перемножимо вирази (13.1) та (13.2). . Остаточно

.

Остача від ділення на 13 дорівнює 8.

Приклад 3.У кільці многочленів з дійсними коефіцієнтами знайти найбільший спільний дільник многочленівта.

Розв’язок.Використовуємо алгоритм Евкліда, який полягає у наступному.

Нехай дані два многочлени таі потрібно знайти їх найбільший спільний дільник.

Поділимо спочатку наз остачею

.

Якщо остача , поділимоназ остачею

.

Якщо остача , поділимона

.

І так далі. Оскільки степінь кожної наступної остачі менше степеня попередньої остачі, то колись процес закінчиться, тобто ділення відбудеться без остачі.

.

Остання ненульова остача у цій процедурі і буде найбільший спільний дільник многочленівта.

Примітка: найбільший спільний дільник многочленів визначається неоднозначно, а з точністю до числового множника. Тому в алгоритмі Евкліда завжди можна уникнути дробових коефіцієнтів, помноживши один з многочленів на деяке число. При цьому найбільший спільний дільник множиться на деяке (взагалі кажучи, інше) число. Але зважаючи на зроблене зауваження, це несуттєво.

Повертаємося до приклада.

Отримали остачу =. Поділимо многочленна .

Найбільший спільний дільник многочленів таце.

Приклад 4.У кільці многочленів з дійсними коефіцієнтами знайти найбільший спільний дільник многочленівта.

Розв’язок. Поділимо на з остачею.

(помножимо на )

Поділимо на першу отриману остачу (скорочену на 5).

Поділимо першу отриману остачу на другу (скорочену на 9).

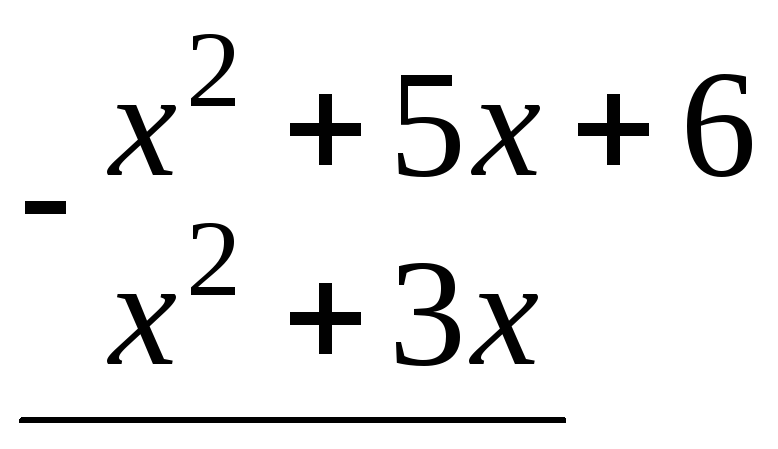
Остання ненульова остача і буде найбільшим спільним дільником.

13.5 Задачі для самостійного розв’язання

1.Використовуючи Малу теорему Ферма, знайти остачу від ділення 1)на 11; 2)на 7; 3)на 19; 4)на 13; 5)на 17; 6)на 5; 7)на 13.

2. У кільці многочленів з дійсними коефіцієнтами знайти найбільший спільний дільник многочленів 1) та; 2) та;

3) та;

4) та;

5) та;

6) та;

7) та;

8) та;

9) та;

10) та.