
- •Міністерство освіти і науки україни
- •1 Множина комплексних чисел. Дії з комплексними числами
- •1.5 Задачі для самостійного розв’язання
- •2.5 Задачі для самостійного розв’язання
- •3 Основні властивості груп
- •3.5 Задачі для самостійного розв’язання
- •4 Підгрупи
- •4.5 Задачі для самостійного розв’язку
- •5 Циклічні групи
- •5.5 Задачі для самостійного розв’язання
- •6 Перестановки
- •6.5 Задачі для самостійного розв’язання
- •7 Гомоморфізм груп
- •7.5 Задачі для самостійного розв’язання
- •8 Суміжні класи
- •8.5 Задачі для самостійного розв’язання
- •9 Фактор-групи
- •9.5 Задачі для самостійного розв’язання
- •10 Основні властивості кілець і полів
- •10.5 Задачі для самостійного розв’язання
- •11 Гомоморфізм кілець. Ідеали
- •11.5 Задачі для самостійного розв’язання
- •12 Операції над ідеалами. Фактор-кільця
- •12.5 Задачі для самостійного розв’язку
- •13 Кільце лишків. Алгоритм евкліда
- •13.5 Задачі для самостійного розв’язання
- •Термінологічний словник
- •Рекомендована література
9.5 Задачі для самостійного розв’язання
1. Розгляньте
фактор-групу![]() .
Доведіть, що операція фактор-групи
визначає на наведеній системі залишків
за модулем
.
Доведіть, що операція фактор-групи
визначає на наведеній системі залишків
за модулем![]()
![]() операцію додавання за модулем
операцію додавання за модулем![]() :
:![]()
![]() .
.
2. Знайти
фактор-групу адитивної групи цілих
чисел, кратних чотирьом![]() за підгрупою цілих чисел, кратних
дванадцяти
за підгрупою цілих чисел, кратних
дванадцяти![]() .
Чи буде фактор-група циклічною? Визначити
її порядок.
.
Чи буде фактор-група циклічною? Визначити
її порядок.
3. Знайти
фактор-групу адитивної групи цілих
чисел, кратних трьом![]() за підгрупою цілих чисел, кратних
дванадцяти
за підгрупою цілих чисел, кратних
дванадцяти![]() .
Чи буде фактор-група циклічною? Визначити
її порядок.
.
Чи буде фактор-група циклічною? Визначити
її порядок.
4. Знайти
фактор-групу адитивної групи цілих
чисел, кратних п’ятьом![]() за підгрупою цілих чисел, кратних
двадцяти
за підгрупою цілих чисел, кратних
двадцяти![]() .
Чи буде фактор-група циклічною? Визначити
її порядок.
.
Чи буде фактор-група циклічною? Визначити
її порядок.
5. Знайти
фактор-групу адитивної групи цілих
чисел, кратних двом![]() за підгрупою цілих чисел, кратних десяти
за підгрупою цілих чисел, кратних десяти![]() .
Чи буде фактор-група циклічною? Визначити
її порядок.
.
Чи буде фактор-група циклічною? Визначити
її порядок.
6. Знайти
фактор-групу мультиплікативної групи
коренів 6-го степеня з одиниці за підгрупою![]() .
.
7. Доведіть,
що фактор-група адитивної групи![]() векторів площини, що виходять із початку
координат, за підгрупою
векторів площини, що виходять із початку
координат, за підгрупою![]() векторів, що лежать на осі
векторів, що лежать на осі![]() ізоморфна групі
ізоморфна групі![]() векторів,
що лежать на осі
векторів,
що лежать на осі![]() .
.
8. Доведіть ізоморфізм зазначених груп:
1)
 ; 2)
; 2) ;
;
3)
 ,
де
,
де![]() –
множина точок, які належать одиничному
колу;
–
множина точок, які належать одиничному
колу;
4)
 ; 5)
; 5)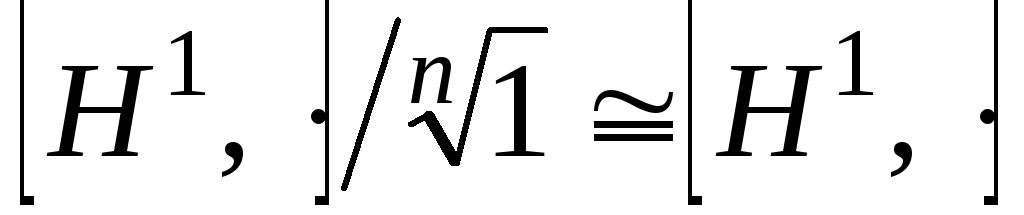 ;
;
6)
 ; 7)
; 7)![]() .
.
8)
![]() ;
9)
;
9)![]() .
.
10 Основні властивості кілець і полів
10.1 Мета заняття
Розглянути конкретні приклади кілець і полів; навчити студентів виконанню операцій у кільцях, особливо в некомутативних; звернути увагу студентів на специфіку кілець, відмінних від числових кілець, передусім, на наявність дільників нуля.
10.2 Методичні вказівки з організації самостійної роботи
За темою «Основні властивості кілець і полів» студент повинен: знати поняття кільця, поля, їхні основні властивості, а також поняття абелевої групи, підкільця, комутативного кільця; вміти роз’язувати задачі за темою [3, c. 172-178].
10.3 Контрольні запитання
1. Що називається кільцем; тілом; полем?
2. У чому відмінність поля від кільця?
10.4 Приклади розв’язання аудиторних задач
Приклад 1. З’ясувати, чи буде множина матриць вигляду
![]()
кільцем або полем відносно звичайних операцій додавання й множення матриць.
Розв’язок.Нагадаємо,
що непуста множина![]() ,
на якій задані дві алгебраїчні операції
додавання і множення, називається
кільцем
,
на якій задані дві алгебраїчні операції
додавання і множення, називається
кільцем ,
якщо виконані три умови:
,
якщо виконані три умови:
1)
![]() – абелева група;
– абелева група;
2)
![]() – полугрупа;
– полугрупа;
3) операції додавання і множення зв’язані дистрибутивним законом:
![]() та
та
![]() .
.
Якщо у кільці множення комутативне, то кільце називається комутативним. Одиничний елемент за додаванням називається нульом кільця, одиничний елемент за множенням – одиницею кільця.
Поле
– це комутативне кільце з одиницею, в
якому міститься не менше двох елементів
і кожен ненульовий елемент має обернений
відносно множення. Тобто щоб алгебраїчна
структура була полем
 ,
необхідно невиконання умов:
,
необхідно невиконання умов:
1)
![]() – абелева група;
– абелева група;
2)
 – абелева група;
– абелева група;
3) операції додавання і множення зв’язані дистрибутивним законом:
![]() та
та
![]() .
.
Перевіримо
![]() .
Перевіряємо аксіоми групи:
.
Перевіряємо аксіоми групи:
1) замкненість даної множини матриць відносно додавання:
![]()
![]()
![]() +
+![]() =
=![]()
![]() , тому що
, тому що![]() та
та![]() ;
;
2) властивість
асоціативності
![]() перевіряти не потрібно, тому що вона
справедливі для будь-якої множини
матриць
перевіряти не потрібно, тому що вона
справедливі для будь-якої множини
матриць![]() ;
;
3) наявність
одиничного елемента
![]() .
Одиничний елемент – нульова матриця
.
Одиничний елемент – нульова матриця![]() ;
;
4) наявність
оберненого елемента
![]() .
Обернений елемент – матриця:
.
Обернений елемент – матриця:![]() ;
;
5)
комутативний закон виконується
![]() .
.
Отже
![]() – абелева група.
– абелева група.
Так
само перевіряємо
![]() .
.
1) замкненість даної множини матриць відносно множення:
![]()
![]()
![]()
![]() =
=![]()
![]() ,
тому що
,
тому що![]() та
та![]() .
.
2) властивість
асоціативності
![]() перевіряти не потрібно, тому що вона
справедлива для будь-якої множини
матриць
перевіряти не потрібно, тому що вона
справедлива для будь-якої множини
матриць![]() .
.
3) одиничний
елемент – одинична матриця
![]() .
.
4) обернений елемент – обернена матриця
![]() .
.
Обернені існують для всіх елементів, крім нульової матриці.
5)
комутативний закон виконується
![]() .
.
![]()
![]()
![]() =
=![]() .
.
Отже
 – абелева група.
– абелева група.
Дистрибутивний
закон теж виконується. Висновок:
 - поле.
- поле.
Приклад 2. Елемент![]() ,
,![]() називається нільпотентним, якщо
називається нільпотентним, якщо![]() .
Довести, що якщо g нільпотентний, то
елемент
.
Довести, що якщо g нільпотентний, то
елемент![]() оборотний.
оборотний.
Розв’язок.Перевіримо,
що![]() є оберненим до
є оберненим до![]() відносно множення. Дійсно,
відносно множення. Дійсно,![]()
![]() ,
тому що
,
тому що![]() .
.
Аналогічно
![]() .
Отже, елемент
.
Отже, елемент![]() оборотний (тобто має обернений відносно
множення) та елемент
оборотний (тобто має обернений відносно
множення) та елемент![]() .
.
Приклад 3. Доведіть, що в довільному, не обов'язково комутативному кільці K справедливі рівності:
1.
![]() ;
;
2.
![]() ;
;
3.
![]() .
.
Доведення.Доведемо, що 1.![]() і
2.
і
2.![]() .
Відомо, що
.
Відомо, що![]() .
Скористаємося дистрибутивністю множення
відносно додавання, одержимо
.
Скористаємося дистрибутивністю множення
відносно додавання, одержимо![]() та
та![]()
![]() .
Із цих рівностей одержимо
.
Із цих рівностей одержимо![]() та
та![]() .
.![]() .
.
Доведемо, що 3. ![]() . Маємо
. Маємо![]() ,
з огляду, що
,
з огляду, що![]() ,
далі одержуємо
,
далі одержуємо![]() .
.
Приклад 4. Доведіть,
що в кільці зnелементів![]() .
.
Розв’язок.За
додаванням кільце – абелева група.
Нехай елемент![]() має порядок
має порядок![]() .
Тоді циклічна підгрупа
.
Тоді циклічна підгрупа![]() має порядок
має порядок![]() .
За теоремою Лагранжа порядок підгрупи
є дільником порядку групи, тобто
.
За теоремою Лагранжа порядок підгрупи
є дільником порядку групи, тобто![]() .
.
Отримуємо,
![]() .
.
Приклад 5. Доведіть,
що якщо![]() ,
,![]() ,
,![]() ,
то
,
то![]() й
й![]() необоротні.
необоротні.
Доведення.Нехай![]() ,
тоді
,
тоді![]() .
Використовуючи асоціативність, запишемо
.
Використовуючи асоціативність, запишемо![]() ,
,![]() ,
,![]() ,
що суперечить умові. Отже, елемент
,
що суперечить умові. Отже, елемент![]() необоротний. Аналогічно доводиться, що
елемент
необоротний. Аналогічно доводиться, що
елемент![]() необоротний.
необоротний.
Приклад 6. Знайдіть всі оборотні елементи кілець:
1)
![]() ;
2)
;
2)![]() .
.
Розв’язок.1. Складемо таблицю Келі для операції множення за модулем 7.
-

0
1
2
3
4
5
6
0
0
0
0
0
0
0
0
1
0
1
2
3
4
5
6
2
0
2
4
6
1
3
5
3
0
3
6
2
5
1
4
4
0
4
1
5
2
6
3
5
0
5
3
1
6
4
2
6
0
6
5
4
3
2
1
З
таблиці Келі випливає, що
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
тобто всі елементи, крім нуля, оборотні.
Отже, множина оборотних елементів кільця
,
тобто всі елементи, крім нуля, оборотні.
Отже, множина оборотних елементів кільця![]() є
є![]() .
.
2.
Для кільця
![]() множина оборотних елементів
множина оборотних елементів![]() ,
що випливає з таблиці Келі.
,
що випливає з таблиці Келі.
-

0
1
2
3
4
5
0
0
0
0
0
0
0
1
0
1
2
3
4
5
2
0
2
4
0
2
4
3
0
3
0
3
0
3
4
0
4
2
0
4
2
5
0
5
4
3
2
1
Приклад 7.Знайдіть
усі підкільця кілець![]() ,
,![]() і
і![]() .
.
Розв’язок.Будь-яка
підгрупа адитивної групи кільця![]() є підкільцем кільця
є підкільцем кільця![]() .
Отже, підкільцями кільця
.
Отже, підкільцями кільця![]() є підгрупи
є підгрупи![]() ,
,![]() ,
,![]() ,
,![]() ;
кільця
;
кільця![]() :
:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
поля
;
поля![]() :
:![]() ,
,![]() .
.
