Основні властивості систем аксіом

1. Несуперечливість. Система аксіом називається несуперечливою, якщо з її аксіом не можна вивести двох суперечливих висловлень A і .

2. Незалежність. Система аксіом називається незалежною, якщо кожна аксіома є незалежною від інших аксіом, тобто її не можна довести на основі решти аксіом.

3. Повнота. Система аксіом називається повною, якщо вона не може бути поповнена, тобто якщо до системи аксіом не можна додати ніякої аксіоми, котра не випливає з них і разом з цим не суперечила їм.

Встановлення вказаних властивостей для конкретної системи аксіом може бути дуже складним. Одним із основних методів їх встановлення ґрунтується на понятті моделі аксіоматичної теорії.

Моделлю аксіоматики називається довільна сукупність деяких об’єктів і відношень між ними, для яких виконуються аксіоми даної аксіоматики.

Приклад 3. Моделлю аксіоматики метричного простору є сукупність дійсних чисел, у якій відстань між числами х і у визначимо формулою (x, y) = |x – y|. За властивостями модуля ця відстань задовольняє аксіоми метричного простору.

Основні твердження

1. Система аксіом несуперечлива, якщо для неї існує несуперечлива модель.

2. В системі аксіом дана аксіома незалежна від інших, якщо існує модель, для якої виконуються всі аксіоми крім цієї.

3. Система аксіом повна, якщо всі її моделі ізоморфні, тобто між кожними двома з них існує взаємнооднозначне відображення, яке зберігає відношення в цих моделях.

Приклад 4. Дослідити властивості аксіоматики метричного простору.

1. Несуперечливість. Система аксіом метричного простору несуперечлива, оскільки існують несуперечливі моделі цієї аксіоматики:

а) (R, |x – y|); б) .

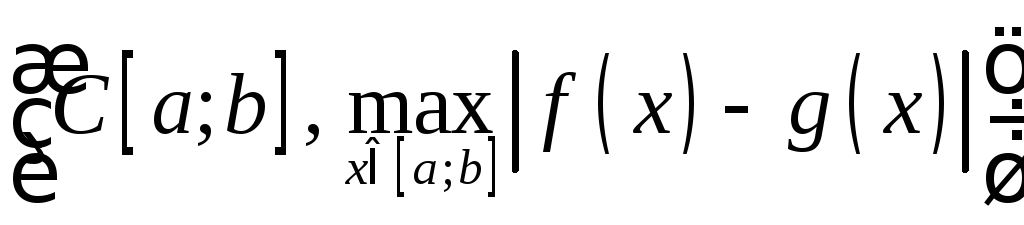2. Незалежність. В моделі (R², ((x₁, y₁), (x₂, y₂)) = |x₁ – x₂|) не виконується аксіома A₁. Аксіома A₂ не виконується в моделях, в яких (x, y) — це час необхідний щоб дійти з x до y.

3. Повнота. Аксіоматика неповна. Існують неізоморфні моделі.

Запитання для осмислення

1. Математика цариця чи служниця?

2. Чи можна дати означення математики?

3. Що складає предмет математики?

4. У чому головна особливість математики як науки?

5. Яку роль відіграє математика у сучасному суспільстві?

6. Що доцільно взяти за основу періодизації розвинення математики?

7. Яка характерна риса кожного періоду?

8. Чи відображають назви періодів їхній зміст?

9. Коли виникла математика?

10. Які існують джерела розвинення математики?

11. Чи є математика наукою для науки?

12. Чим пояснюється універсальність математики?

13. Чи існують чиста і прикладна математики?

14. До чистої чи прикладної математики належить: 1) теорія диференціальних рівнянь; 2) теорія ймовірностей; 3) теорія чисел; 4) теорія банохових просторів.

15. Що таке математична модель?

16. У чому полягає математичне моделювання?

17. Чи може кришка столу бути паралелепіпедом?

18. Чи можна дати означення неозначованому поняттю?

19. Чи можна довести аксіому?

20. Чи може теорема бути хибною?

21. Чи доводить тисячолітній досвід істинність аксіом евклідової геометрії?

Індивідуальне завдання №1.

Метод математичного моделювання.

Мета. Усвідомити сутність метода математичного моделювання, оволодіти навичками розв’язання прикладних задач за певною схемою.

Завдання

Виберіть прикладну задачу, розв’язання якої є яскравою ілюстрацією метода математичного моделювання, тобто:

1) побудова математичної моделі потребує розгляду певних умов, припущень;

2) дослідження математичної моделі складається з розв’язання нетривіальної математичної задачі;

3) аналіз та інтерпретація результатів дослідження супроводжується розглядом ускладненої математичної моделі.

Розв’язок задачі необхідно оформити у відповідності з вказаною схемою, чітко фіксуючи відповідні етапи.

Теми для доповідей і рефератів

1. Що таке математика?

2. Основні етапи розвинення математики.

3. Прикладна математика.

4. Жорсткі і м’які математичні моделі.

5. Про книгу Д.Гільберта „Основи геометрії”.

6. Чи існує математик Бурбакі?

7. Ерлангенська програма Клейна.

8. Неевклідові геометрії.

9. Методологічні основи математики.

Література до розділу 1

1. Александров А. Д. Основания геометрии. М.: Наука, 1980.

1. Блехман И. И., Мышкис А. Д., Пановко Я. Г. Механика и прикладная математика. М.: Наука 1990.

2. Бурбаки Н. Очерки по истории математики. — М.: ИЛ, 1963.

3. Введение в математическое моделирование/ Под ред. Трусова. — М.: Логос, 2004.

4. Гнеденко Б. В. Введение в специальность математики. М.: Просвещение, 1991.

5. Гильберт Д. Основания геометрии. — М. — Л., Гостехиздат, 1948.

6. Колмогоров А. Н. Математика в её историческом развитии. — М.: Наука, 1991.

7. Курант Р. Роббинс Г. Что такое математика. — М.: Просвещение, 1967.

8. Математическое моделирование/ Под ред. Дж. Эндрюса и Р.Мак-Лоуна. — М.: Мысль, 1979.

9. Рузавин Г. И. О природе математического знания. — М.: 1968.

10. Стройк Д. Я. Краткий очерк истории математики. — М.: Наука, 1969.

11. Тихонов А. Н., Костомаров Д. П. Вводные лекции по прикладной математике. — М.: Наука 1984.

12. Яглом И. М. Математические структуры и математическое моделирование. — М.: Советское радио, 1980.