231. 232.

233. 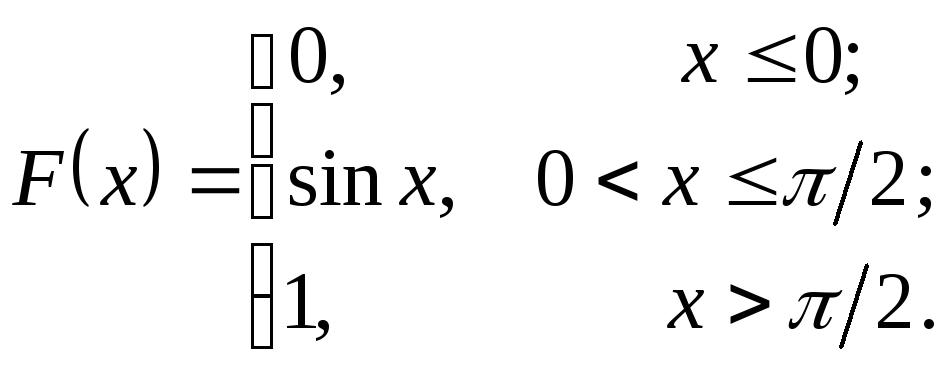234.

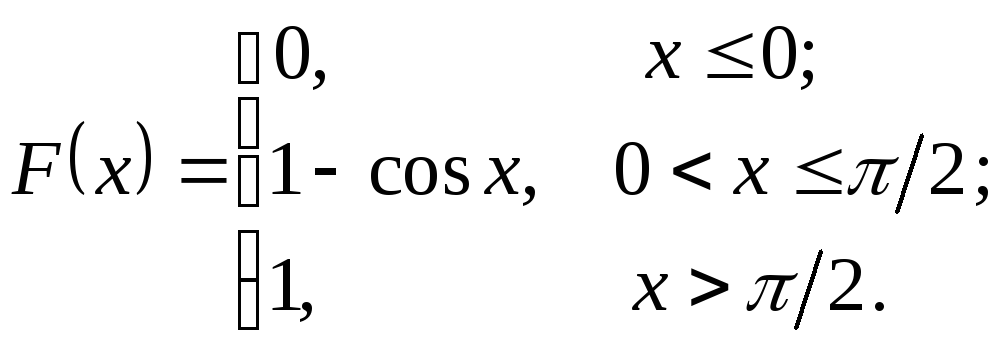
235. 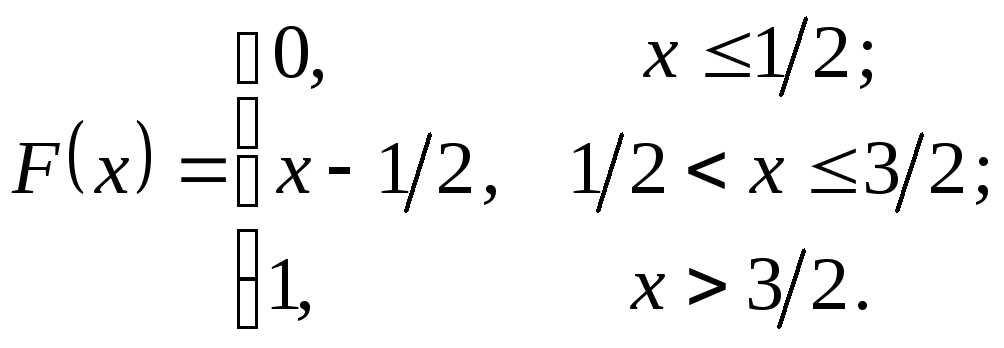236.

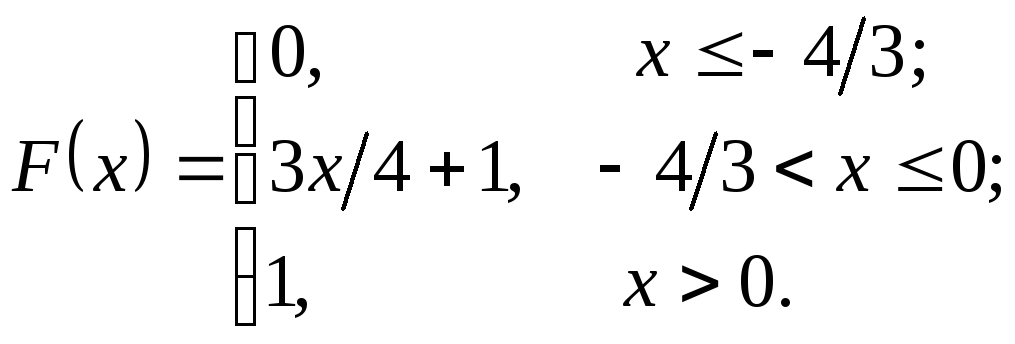
237. 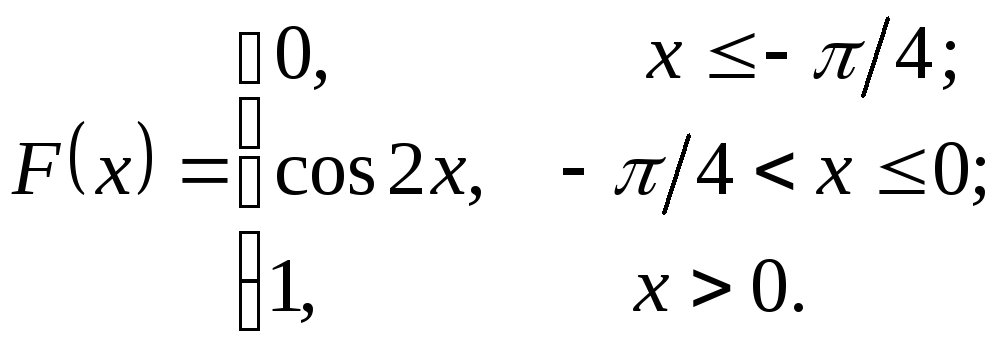238.

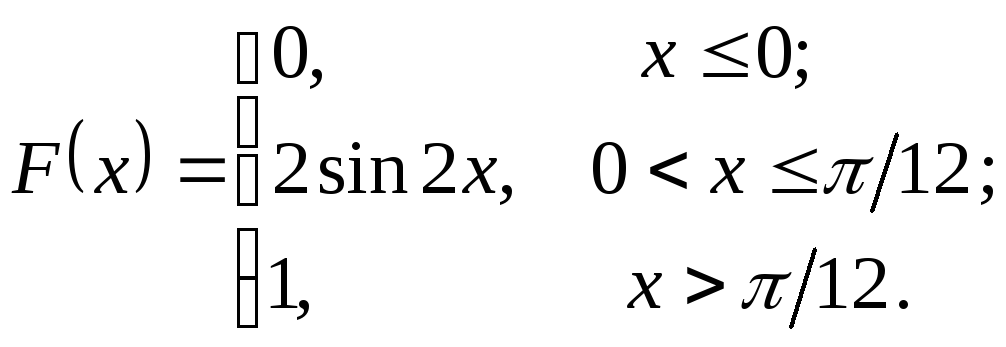
239. 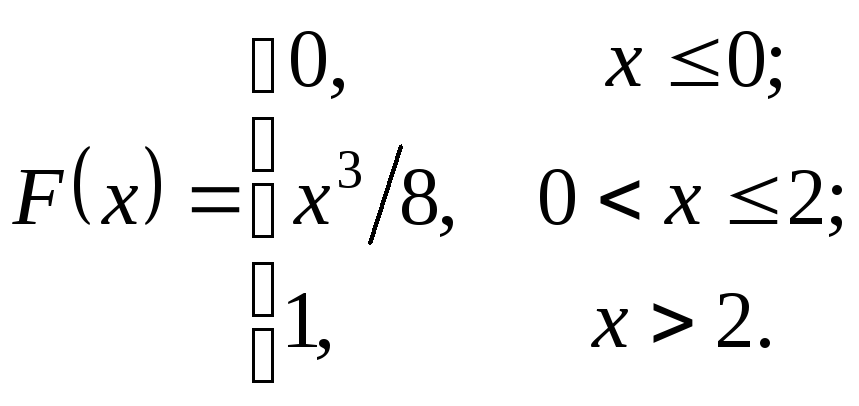240.

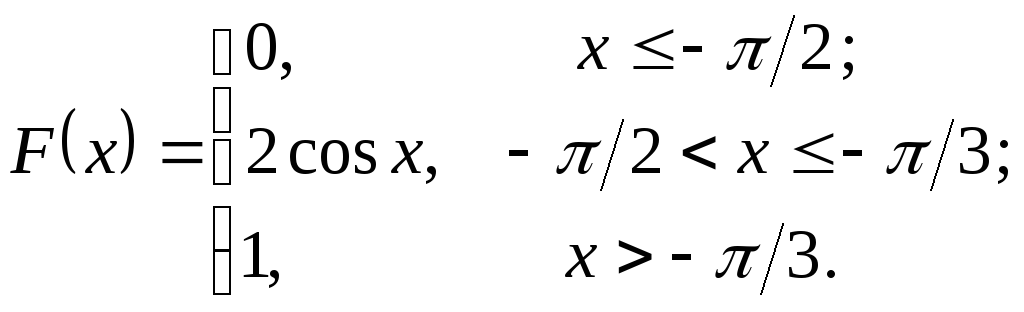
Пример.Случайная величиназадана функцией распределенияF(x).Найти плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины.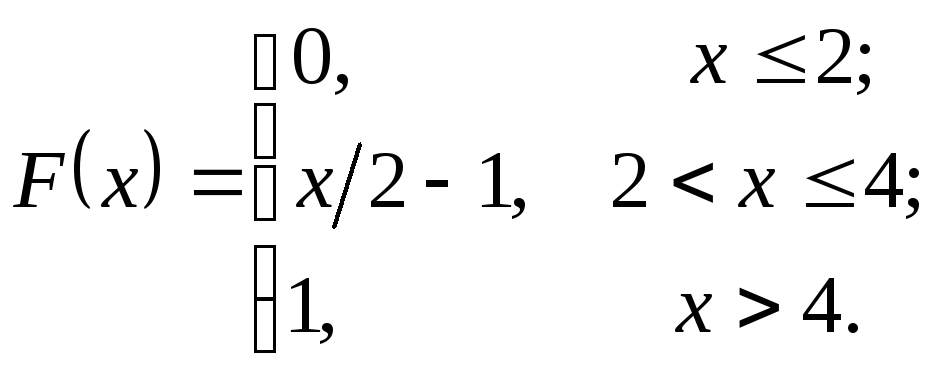

Найдем плотность распределения:

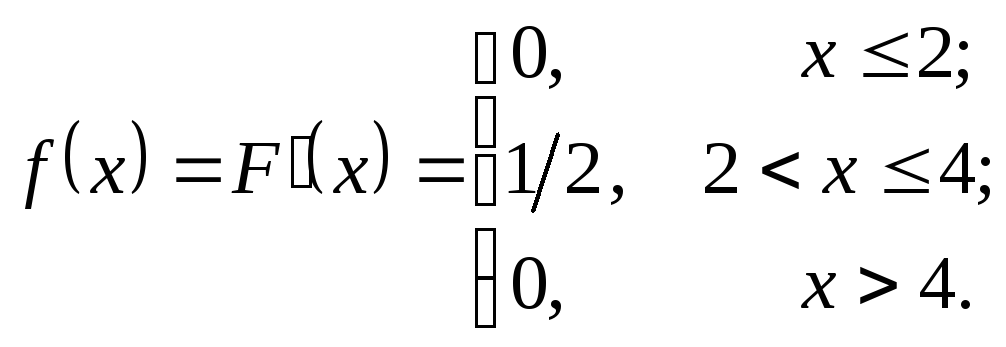
Используя определения математического ожидания и дисперсии для непрерывных случайных величин:

, ,

получаем:

241. Плотность распределения случайной величиныимеет вид:

.

Найти: ,,.

242. Случайная величина имеет нормальное распределение с плотностью:

.

Найти: ,,.

243.Плотность распределения случайной величины имеет вид:

.

Найти: ,,.

244. Плотность распределения случайной величины имеет вид:

.

Найти: ,,.

245.Плотность распределения случайной величины имеет вид:

.

Найти: ,,.

246. Плотность распределения случайной величины имеет вид:

.

Найти: ,, .

247. Случайная величинаимеет плотность распределения:

.

Найти: ,,.

248. Функция распределения случайной величины имеет вид:

.

Найти: ,,.

249. Плотность распределения случайной величины имеет вид:

.

Найти: ,,.

250. Случайная величина имеет нормальное распределение с плотностью:

.

Найти: ,,.

Пример.Плотность распределения случайной величины имеет вид:

.

Найти: ,,,.

Нормально распределенная случайная величина имеет плотность распределения:

,

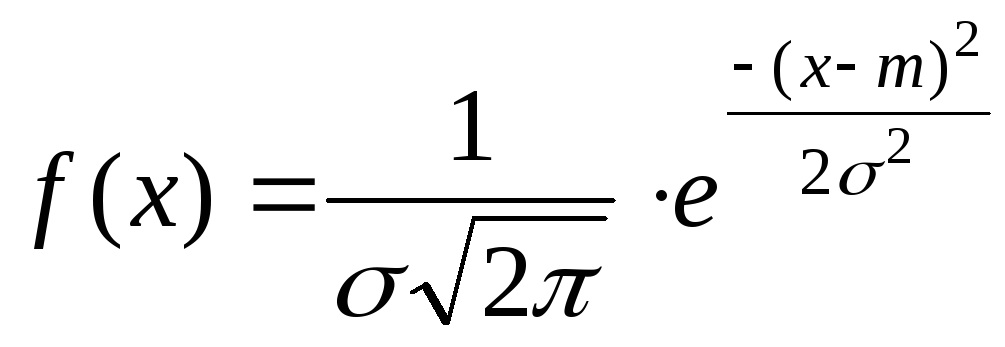где математическое ожидание, дисперсия.

В нашем примере ;.

Для нормальной случайной величины вероятность равна:

.

.

;

.

251-260.Из партии вобразцов бетона путем бесповторной выборки отобранообразцов. Измерения прочности отобранных деталей дали выборочное среднееМПа и выборочное среднее квадратическое отклонениеМПа. Некондиционными признанообразцов. С вероятностьюнайти:

1. Доверительный интервал для генеральной средней .

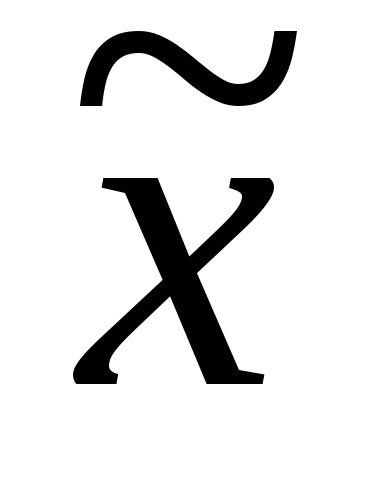2. Доверительный интервал для генеральной доли некондиционных изделий .

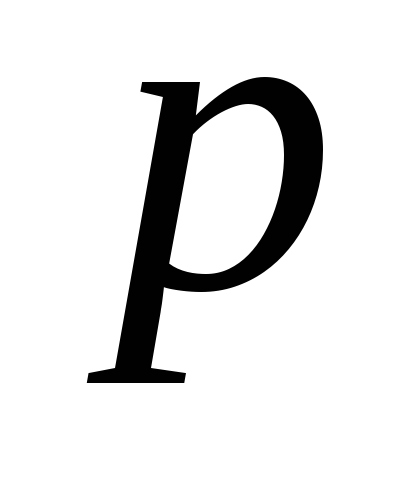01.
02.
03.
04.
05.
06.
07.
08.
09.
110.

Пример. Из 1000 образцов бетона для контроля прочности бесповторным путем отобрали 200 образцов. Изучение выборочной совокупности дало величину выборочной среднейМПа и выборочное среднее квадратическое отклонение МПа. Двадцать образцов признано некондиционными (не соответствующими стандартам качества).

Найти:

а) с вероятностью 0,95 доверительный интервал для генеральной средней;

б) с вероятностью 0,954 долю некондиционных изделий в генеральной совокупности.

а) По условию, ,.

Доверительный интервал для генеральной средней имеет границы:

,

где - предельная ошибка для бесповторной выборки

.

Параметр определяется из равенства, или. По таблице функции Лапласа находят аргумент, которому соответствует значение функции Лапласа, равное.

В нашем примере .

(МПа).

Тогда доверительный интервал для нашего примера:

;

.

С вероятностью 0,95 (в строительстве применяют термин надежность) генеральная средняя прочности бетона находится от 49,752 МПа до 50,248 МПа, т.е. с надежностью 0,95 прочность образцов лежит в найденном интервале. На практике при вычислении доверительного интервала для прочности используется нижняя граница интервала, т.к. нас интересует большая прочность. Тогда прочность образцов будет больше, чем , с вероятностью.

В нашей задаче прочность будет больше, чем 49,752, с вероятностью 0,025.

б) .

Выборочная доля некондиционных изделий

.

Предельная ошибка для генеральной доли

С вероятностью 0,95 доля некондиционных изделий во всей партии составляет от 6,28% до 13,72%.

261-270. С целью изучения статистического признака Х проведено исследование. Результаты представлены в таблице. Определить:

1. среднее значение признака Х;

2. дисперсию, среднее квадратическое отклонение;

3. коэффициент вариации;

4. моду признака Х (аналитически и графически);

5. медиану признака Х (аналитически и графически).

261.Распределение рабочих цеха по возрасту.

Возраст (X), годы	17 - 20	20 - 30	30 - 40	40 - 50	50 - 59	всего
Количество рабочих	29	40	14	11	6	100

262.Распределение рабочих по стажу работы.

Стаж работы (X), годы	до 5	5-10	10-15	15-20	20-25	25-30	св. 30	всего
Кол - во рабочих	11	19	40	25	15	6	4	120

263.Распределение студентов по росту.

Рост (X) в (см)	до 164	164-168	168-172	172-176	176-180	180-184	св. 184	всего
кол-во	12	18	22	31	27	22	8	140

264.Распределение рабочих цеха по уровню зарплаты.

Зар. пл. (X), (грн.)	100-110	110-120	120-130	130-140	140-150	150-160	160-170	всего
Число рабочих	5	10	20	25	20	15	5	100

265.Распределение рабочих механического завода по общему стажу работы.

Общий стаж (лет)	до 5	5-10	10-15	15-20	20-25	25 и более	итого
Число рабочих	35	25	15	11	9	5	100

266.Распределение рабочих цеха по производительности труда.

Производительность труда (%)	до 100	100-102	102-104	104-106	106-108	св. 108	итого
Число рабочих	11	21	37	24	5	2	100

267.Распределение рабочих по уровню зарплаты.

Зарплата (грн.)	до 100	100-120	120-140	140-160	160-180	180-200	св. 200	итого
Число рабочих	7	13	20	40	34	26	10	150

268.Распределение рабочих по выработке изделий за смену.

Кол-во изделий, (шт.)	до 60	60-70	70-80	80-90	90-100	итого
Число рабочих (чел.)	10	20	50	15	5	100

269.Распределение рабочих по возрасту.

Возраст, (годы)	18-20	20-30	30-40	40-50	50-60	св. 60	итого
Число рабочих, (чел)	3	18	42	25	7	5	100

270.Распределение рабочих по уровню зарплаты.

Зарплата, (грн.)	до 150	150-160	160-170	170-180	180-190	190-200	св. 200	итого
Число рабочих	11	14	23	37	15	12	8	120

Пример. Распределение рабочих предприятия по уровню зарплаты.

Зарплата (грн.),	до 150	150-170	170-190	190-210	210-230	св.230	итого
Число рабочих (чел.),	11	14	25	40	17	13	120

Основной характеристикой вариационного ряда является среднее значение (среднее арифметическое взвешенное) Среднее значение находится по формуле:

Для интервальных рядов в качестве значений вариант берутся середины интервалов. Найдем среднее значение для вышеуказанного ряда. В качестве берется значение 140 грн. (первый интервал считается 130-150),равно 240 грн.

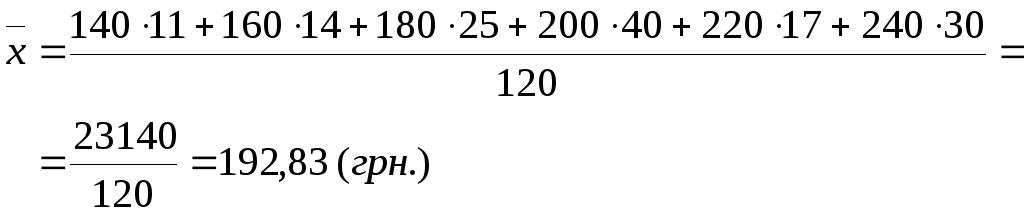
Средняя зарплата на данном предприятии 192,83 грн. Выборки, имеющие одинаковые средние могут значительно отличаться друг от друга по степени разброса (вариации). Для оценки вариации применяется дисперсия:

Вычислим дисперсию для приведенного распределения

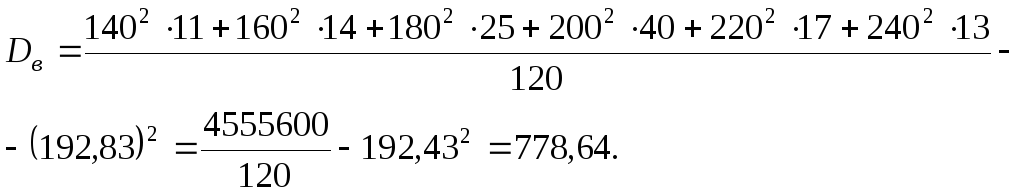
Корень квадратный из дисперсии называется среднеквадратическим отклонением.

В рассматриваемом примере

Для проверки однородности выборки применяется коэффициент вариации:

В тех случаях, когда выборку можно считать однородной.

Для примера

Вышеприведенную выборку можно считать однородной.

Модой распределения называется наиболее часто встречающаяся варианта. Для интервального ряда мода находится по формуле:

где начало модального интервала, т.е. интервала, имеющего наибольшую частоту,длина модального интервала,частота предмодального интервала,частота послемодального интервала.

В рассматриваемом примере модальный интервал

На рассматриваемом предприятии наиболее часто встречается зарплата 197,89 грн.

Графически мода находится с помощью гистограммы. Модальным является наибольший прямоугольник.

Медианой называется варианта, делящая вариационный ряд пополам, т.е. количество вариант, меньших медианы и больших медианы, равны между собой. Для нахождения медианы необходимо понятие накопленной частоты.

Накопленной частотой называется сумма вариант, меньших

Для указанного распределения напишем накопленные частоты.

	130-150	150-170	170-190	190-210	210-230	230-250
	11	14	25	40	17	13
	11	11+14=25	11+14+25==50	50+40=90	90+17= =107	107+13=120

Медианным называется интервал, в котором накопленная частота впервые принимает половину объема выборки в примере медианный интервалгрн. Формула вычисления медианы

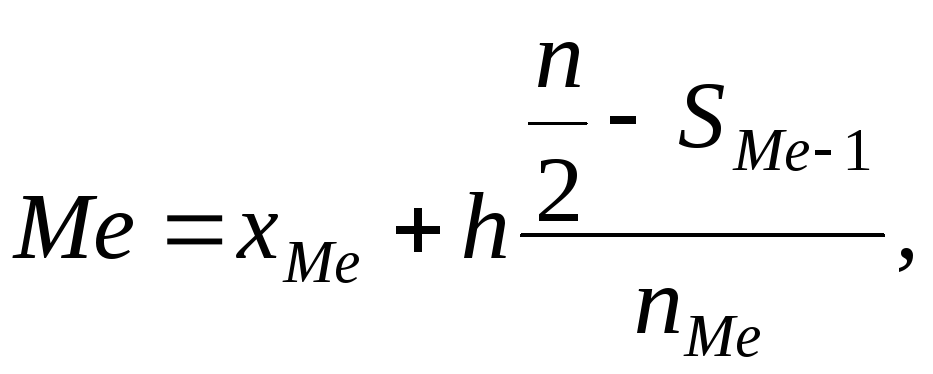
где начало медианного интервала,длина медианного интервала,частота медианного интервала,накопленная частота предмодального интервала. В примере

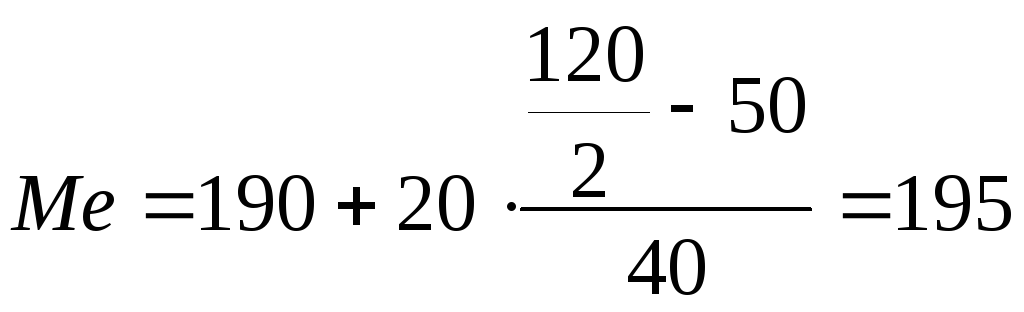(грн.)

Количество рабочих с зарплатой менее 195 грн. и более равны между собой.

Г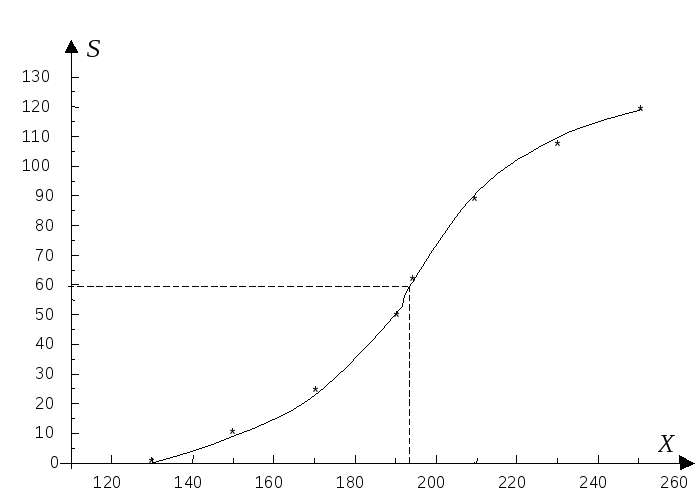рафически медиана находится из графика:

271-280. Составить уравнение линейной регрессии, найти коэффициент корреляции и сделать вывод о связиХиY. Нанести прямую регрессии на корреляционное поле.

271.

	2	3	4	5	6	7	8
	3	5	5,5	4	7	7,5	8,5

272.

	5	2	4	6	7	3	5	6
	10	18	14	8	5	15	8	5

273.

	8	7,5	6	8,2	7,5	6,5	5,5
	3	2,5	1,5	3,5	3	2,5	1,5

274.

	1,7	2,4	3	3,5	2,5	2	1,5	4
	3	5	6,2	7,1	3,5	2,8	1,5	8,2

275.

	10	12	8	15	14	16	12	13
	5,5	6,2	3,9	8	7,5	8,5	5	6,2

276.

	3,7	4,2	3,9	4,3	5	5,2	5,3
	11	12,4	15,2	16,6	17,2	18,1	19,2

277.

	5,2	7,1	8,1	9,2	10,2	11,3	11,5
	10,5	14,3	18,5	20,3	22,1	24,2	25,2

278.

	12,2	14,3	10,6	8,2	9,5	14,2	18,1	22,2
	6,5	7,5	5,8	4,7	5,1	7,2	10,2	12,1

279.

	36	24	18	25	31	33	24
	108	63	47	80	92	102	71

280.

	5,9	7,2	6,1	10,2	14,2	15,1	16,8	19,2	20,1
	6	5,4	4,3	8,3	12,1	12,4	13,2	15,1	18,2

Пример. Имеются выборочные данные по 10 однородным предприятиям

Электровооруженность труда на одного рабочего, квт/ч (х)	22	55	33	77	22	66	44	99	88	44
Выпуск готовой продукции на раб., т (y)	33	66	44	46	64	88	66	99	99	55

Линейная регрессия выражается уравнением прямой (линейной функцией) вида:

;

Коэффициенты уравнения регрессии могут быть найдены методом наименьших квадратов.

Сущность метода наименьших квадратов заключается в нахождении параметров модели , при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по выбранному уравнению регрессии

Пусть имеются данные о признаках X и Y

X1 X2 ... Xi ... Xn

Y1 Y2 ... Yi ... Yn

Для линейной зависимости

S=

Возьмем частные производные по и:

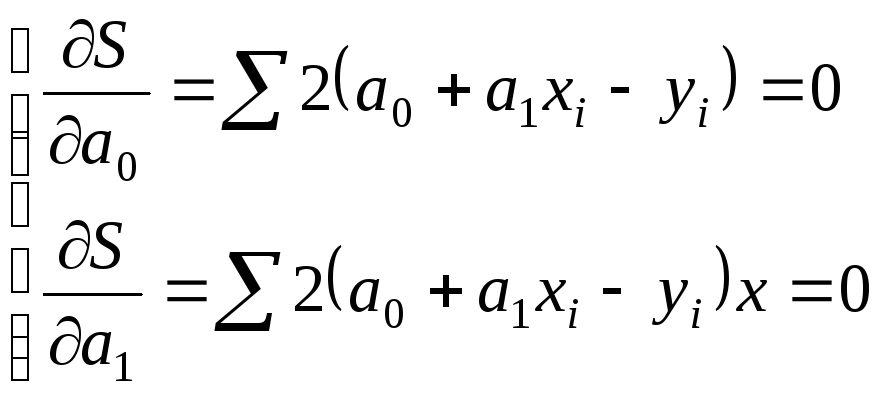
Откуда система нормальных уравнений для нахождения линейной парной регреcсии имеет следующий вид:

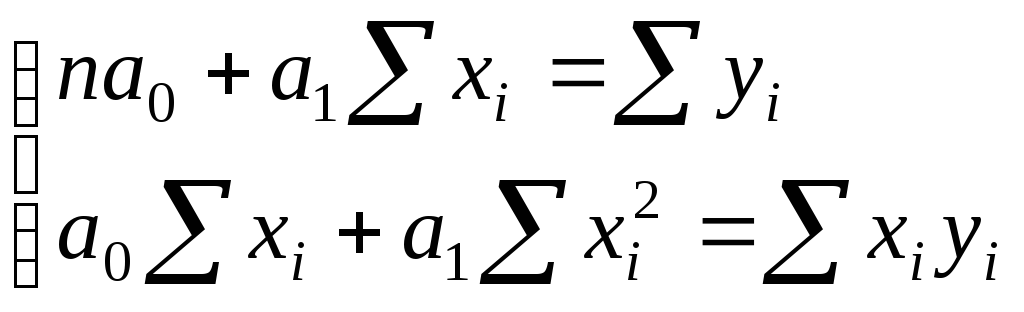
Показателем тесноты линейной связи между факторным и результативным признаком является выборочный коэффициент корреляции.

Коэффициент корреляции вычисляется по формуле:

Раскрыв данное соотношение, можем получить его в другой форме:

Данная формула может быть преобразована к виду:

или

.

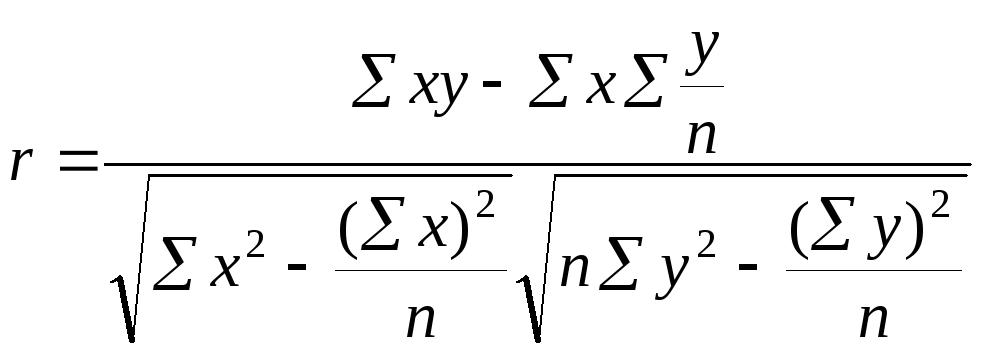Для коэффициента корреляции выполняется . Если, то между x и y прямая связь (чем больше x, тем больше y), если, то между x и y обратная связь (чем больше x, тем меньше y).

Если , то между x и y практически отсутствует связь, близкая к линейной, если, то между x и y умеренная связь, если, то между x и y функциональная связь.

При помощи коэффициента корреляции уравнение линейной регрессии может быть записано в виде:

.

Вернемся к решению задачи.

Составим расчетную таблицу:

X	y	xy	x2	y2	yx	(y-yx)2
2 5 3 7 2 6 4 9 8 4	3 6 4 6 4 8 6 9 9 5	6 30 12 42 8 48 24 81 72 20	4 25 9 49 4 36 16 81 64 16	9 36 16 36 16 64 36 81 81 25	3,61 6,01 4,41 7,60 3,61 6,80 5,20 9,18 8,38 5,20	0,3721 0,0001 0,1682 2,56 0,1521 1,44 0,64 0,0324 0,381 0,04
 = 50	60	343	304	400	60	5,761
среднее=5	6	34,3	30,4	40,0	6,0	0,5761

;

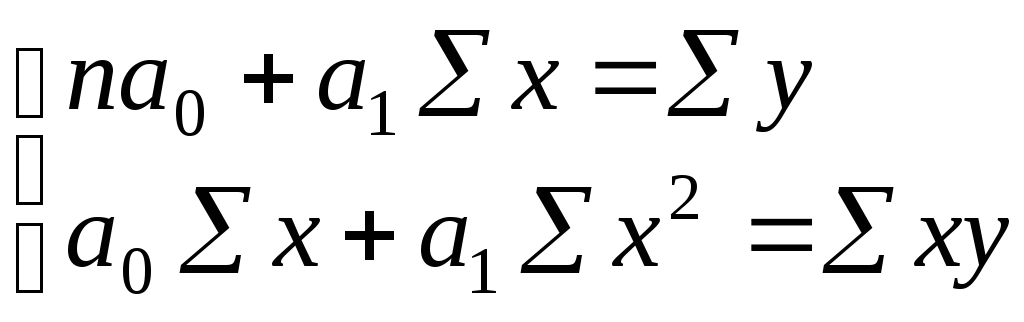
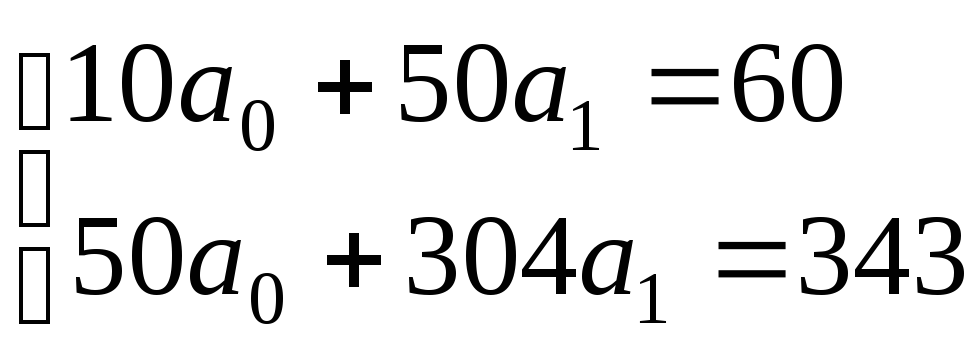решая систему уравнений, получаем решения:

.

.

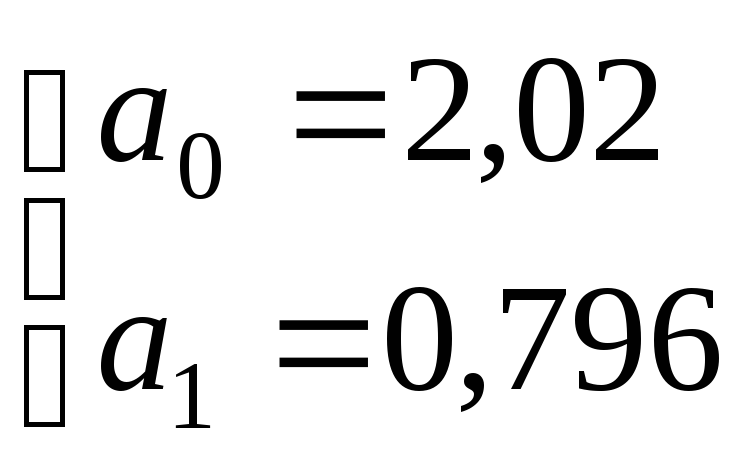Коэффициент корреляции:

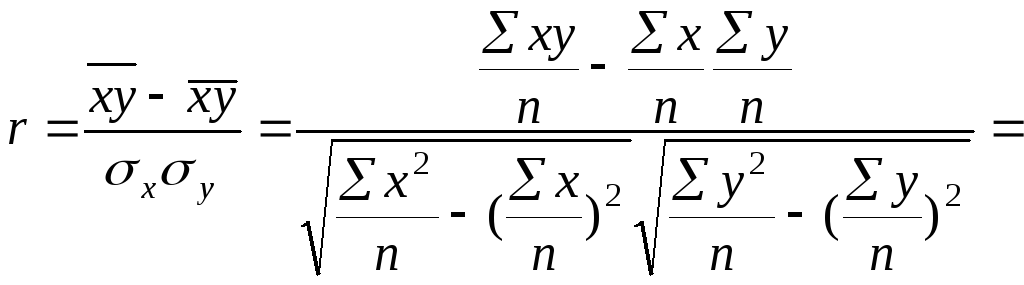
Т.к. , то взаимосвязь междупрямая;близок к 1 - тесная (функциональная) связь.

Нанесем график уравнения регрессии на корреляционное поле: