
- •Предисловие
- •Общие рекомендации студенту-заочнику по работе над курсом высшей математики
- •Чтение учебника
- •Решение задач
- •Самопроверка
- •Консультации
- •Контрольные работы
- •Лекции, практические занятия.
- •Зачеты и экзамены
- •Вопросы для самопроверки Тема I. Векторная алгебра.
- •Тема II. Элементы линейной алгебры.
- •Тема III. Введение в математический анализ.
- •Тема IV. Производная и дифференциал.
- •Тема V. Возрастание и убывание функций. Экстремумы.
- •Тема VI. Построение графиков функций.
- •Тема VII. Неопределенный интеграл.
- •Тема VIII. Определенный интеграл.
- •Тема IX. Обыкновенные дифференциальные уравнения.
- •Тема X. Ряды.
- •Тема XI. Теория вероятностей.
- •Тема XII. Элементы математической статистики.
- •Литература
- •Задачи для контрольных заданий Элементы аналитической геометрии и векторной алгебры
- •Элементы линейной алгебры
- •Введение в математический анализ Раздел Функция.
- •Производная
- •Приложения производной
- •Приложение производной в экономике
- •81. 86.
- •Исследование функций и построение графиков
- •Неопределённый и определённый интегралы
- •121. ,. 126.
- •151. 152.
- •Теория вероятностей и математическая статистика
- •221. Закон распределения случайной величины имеет вид:
- •231. 232.
- •244. Плотность распределения случайной величины имеет вид:
- •248. Функция распределения случайной величины имеет вид:
- •249. Плотность распределения случайной величины имеет вид:
- •250. Случайная величина имеет нормальное распределение с плотностью:
121. ,. 126.
122.
![]() ,
,
![]() .
127.
.
127.
![]()
123.
![]() ,
,
![]() .
128.
.
128.
![]()
124.
![]() ,
,
![]() .
129.
.
129.
![]()
125.
![]() ,
,
![]() .
130.
.
130.
![]()
Пример.
а) Вычислить площадь
фигуры, ограниченной параболой
![]() и прямой
и прямой![]() .
.
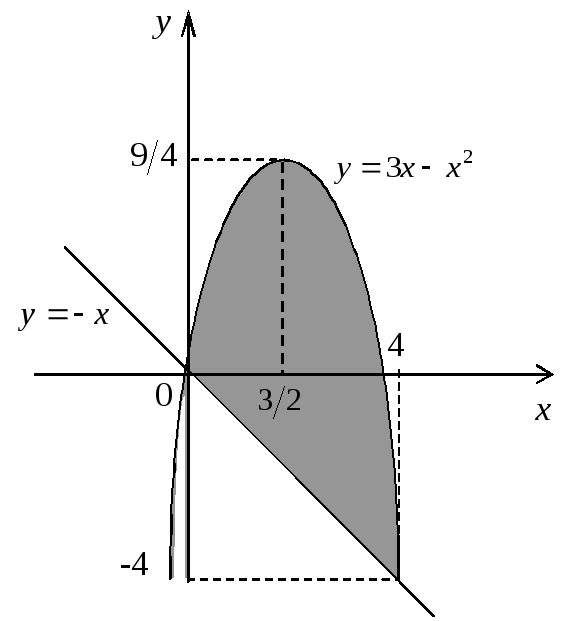
Находим точки пересечения данных кривых и строим искомую фигуру
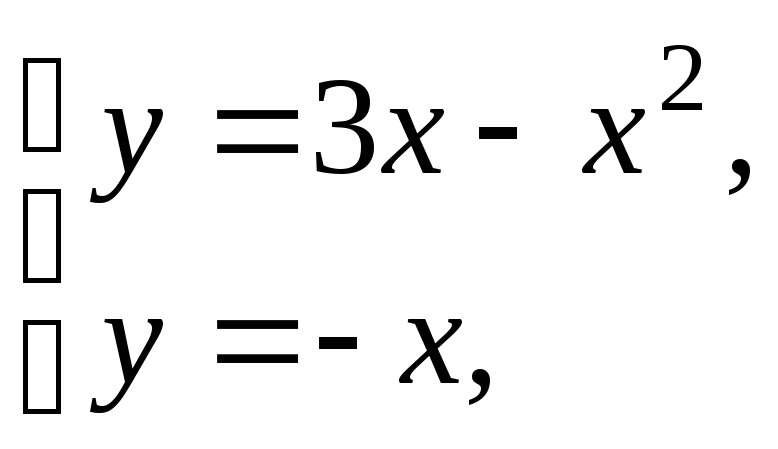
![]()
Площадь фигуры,
ограниченной снизу кривой
![]() ,
сверху – кривой
,
сверху – кривой![]() ,вычисляет интеграл
,вычисляет интеграл
![]() ,
где
,
где![]() и
и![]() - абсциссы точек пересечения этих кривых,
причем
- абсциссы точек пересечения этих кривых,
причем![]()
Следовательно, имеем
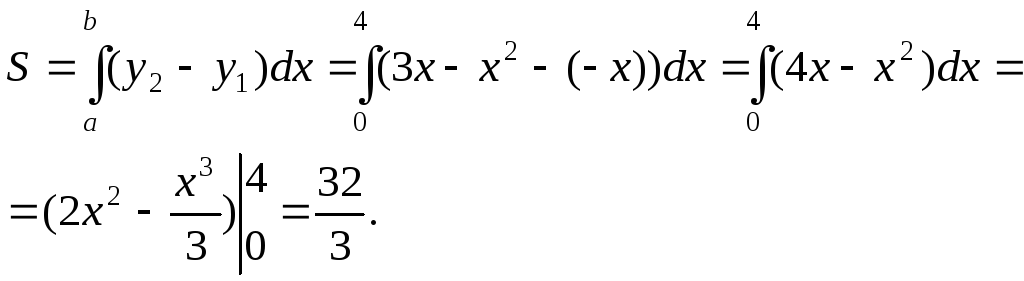
Дифференциальные уравнения.
131 – 140. Найти общее решение дифференциального уравнения.
131.
а).
![]() ;
б).
;
б).
![]() ;
в).
;
в).
![]() .
.
132.
а).
![]() ;
б).
;
б).
![]() ;
в).
;
в).
![]() .
.
133.
а).
![]() ;
б).
;
б).
![]() ;
в).
;
в). ![]() .
.
134.
а).
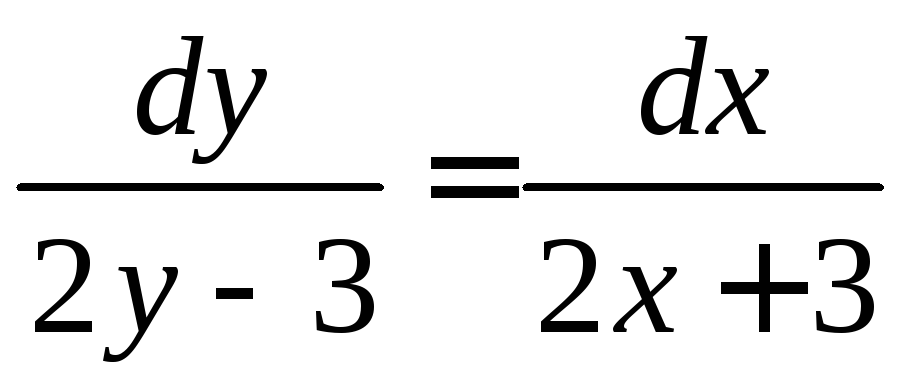 ;
б).
;
б).
![]() ;
в).
;
в).
![]() .
.
135.
а).
 ;
б).
;
б).
![]() ;
в).
;
в).
![]() .
.
136.
а).
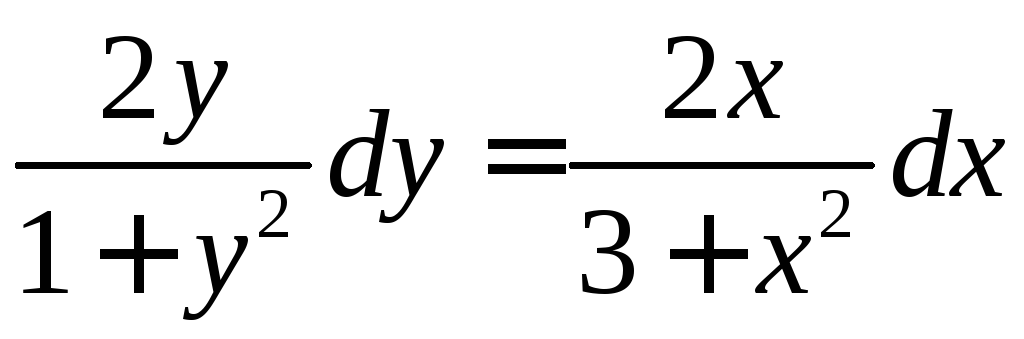 ;
б).
;
б).
![]() ;
в).
;
в).![]() .
.
137.
а).
![]() ;
б).
;
б).![]() ;
в).
;
в).![]() .
.
138.
а).
 ;
б).
;
б).
![]() ;
в).
;
в).
![]() .
.
139.
а).
![]() ;
б).
;
б).
![]() ;
в).
;
в). ![]() .
.
140.
а).
![]() ;
б).
;
б).![]() ;
в).
;
в).
![]() .
.
Пример.
а)
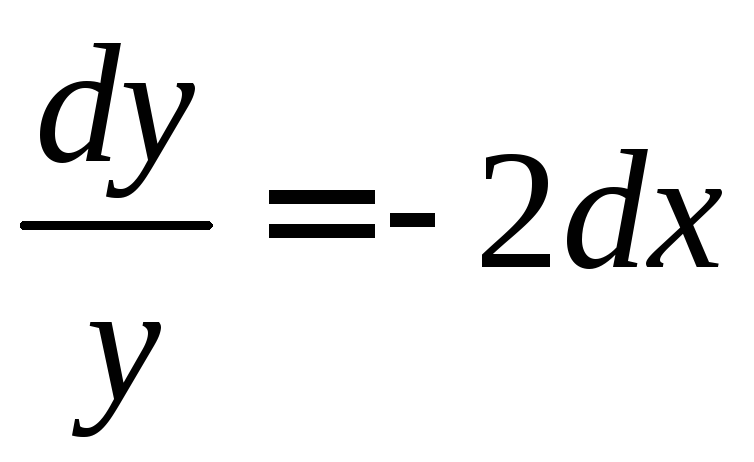 .
.
Данное уравнение является уравнением с разделенными переменными. Проинтегрируем обе его части:
![]() ,
получим:
,
получим:
![]() .
.
б).
![]() .
.
Для решения данного
уравнения используем тот факт, что
![]() .
Так как переменные в данном случае
разделить нельзя, то выразим
.
Так как переменные в данном случае
разделить нельзя, то выразим![]()
![]() ,
отсюда по правилу пропорции получаем:
,
отсюда по правилу пропорции получаем:
![]() ,
или
,
или
![]() .
.
В данном случае![]() ;
;
![]() .
.
Следовательно, данное уравнение – однородное. Делаем замену переменной
![]() ,
,
![]() ,
,
![]() .
После замены получим:
.
После замены получим:
![]() ,
,
![]() ,
,
![]() .
.
Получили уравнение
с разделяющимися переменными. Разделяя
переменные, получим:
![]() ,
,
![]() .
.
Интегрируя, находим общее решение
![]() ,
,![]() ,
,
![]() .
.
Возвращаясь к старой переменной, получаем общий интеграл
![]() .
.
в).
![]() .
.
Данное уравнение
линейное. Ищем решение в виде
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
Решаем уравнение.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Подставляя
полученное значение
![]() в уравнение, имеем:
в уравнение, имеем:
![]() ,
,
![]() ,
,
![]() .
.
Общее решение
![]() или
или![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
141–150. Найти общее решение дифференциального уравнения:
а).
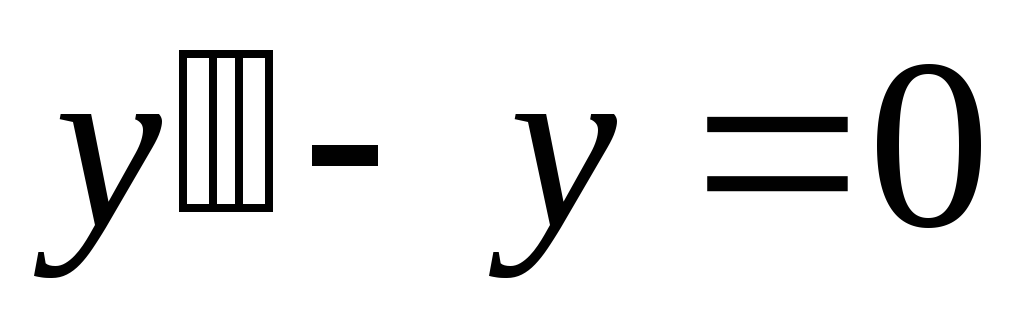 ;
б).
;
б).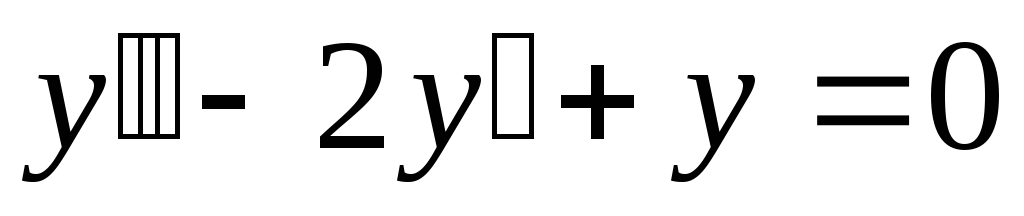 ;
в).
;
в).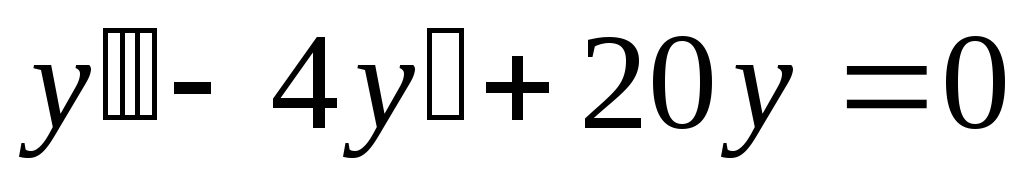 .
.а).
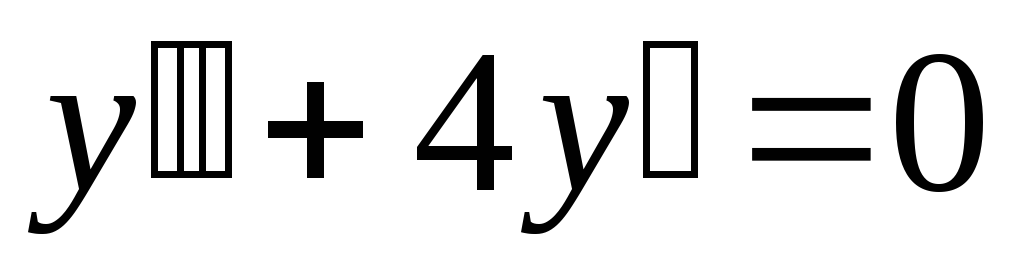 ;
б).
;
б).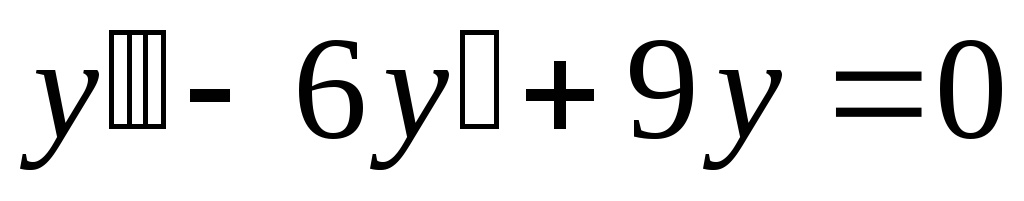 ;
в).
;
в).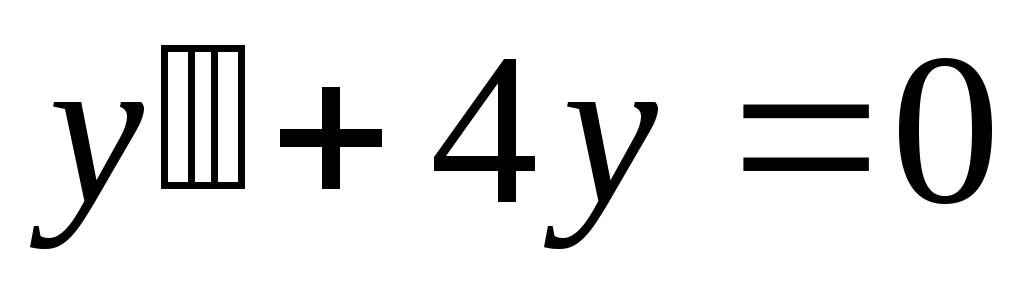 .
.а).
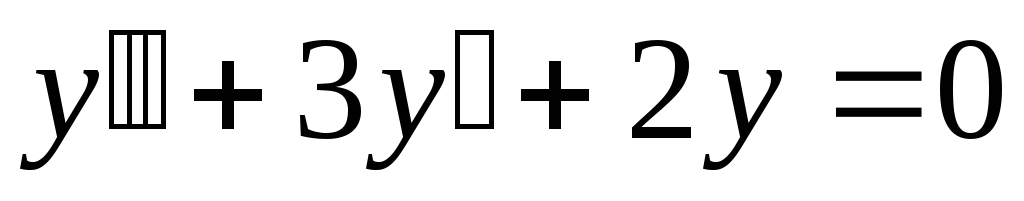 ;
б).
;
б). ;
в).
;
в).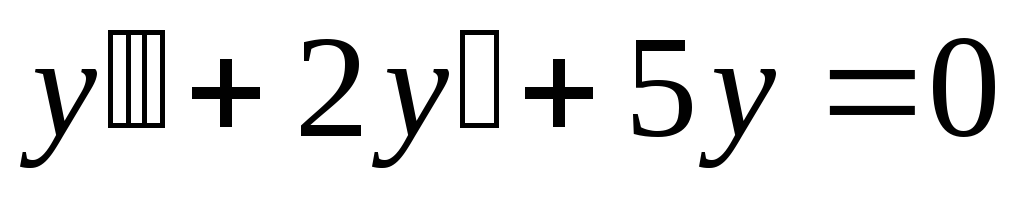 .
.а).
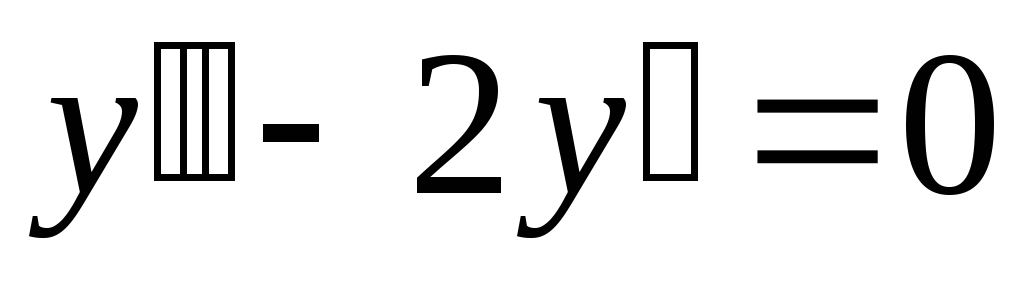 ;
б).
;
б).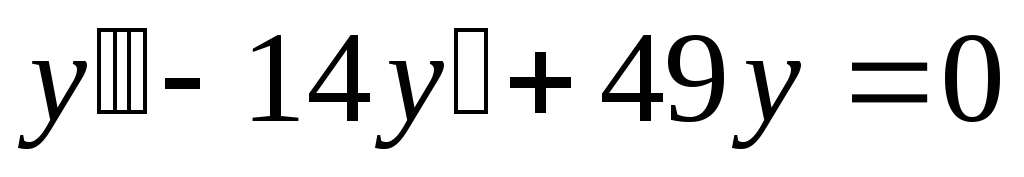 ;
в).
;
в).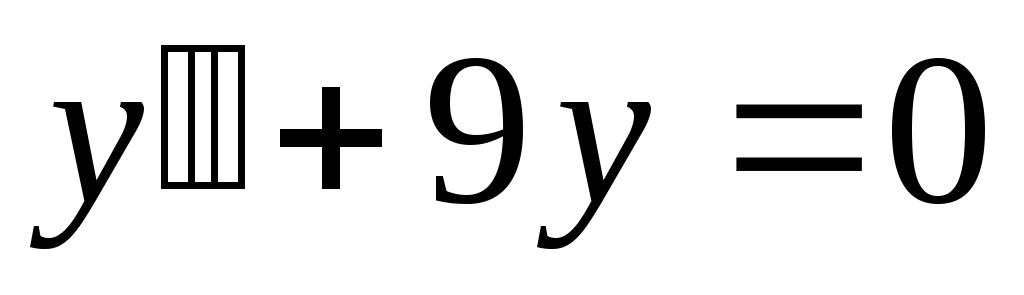 .
.а).
 ;
б).
;
б). ;
в).
;
в).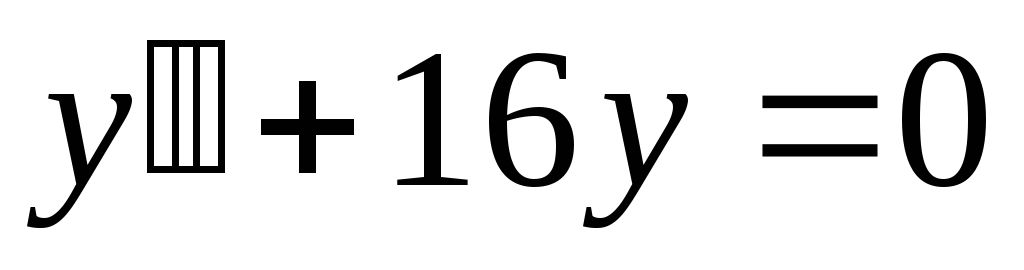 .
.а).
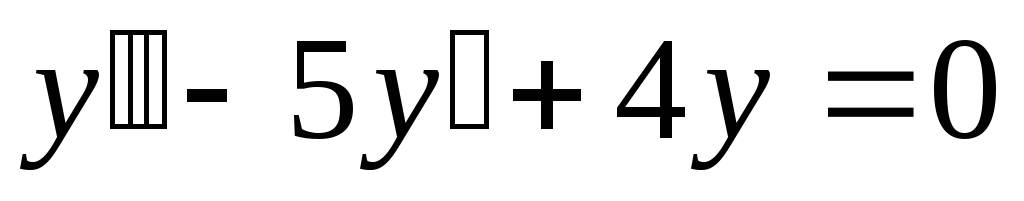 ;
б).
;
б).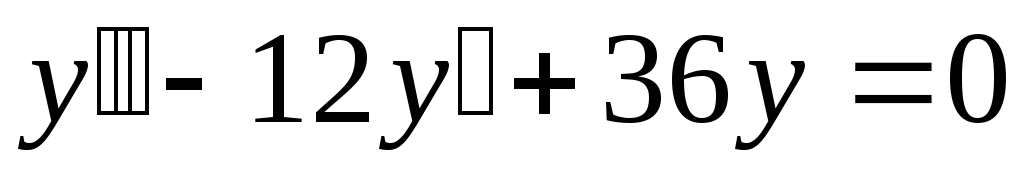 ;
в).
;
в).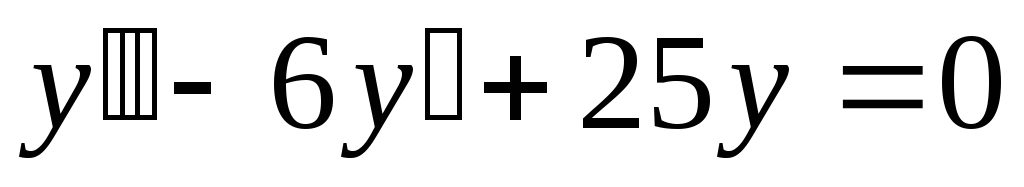 .
.а).
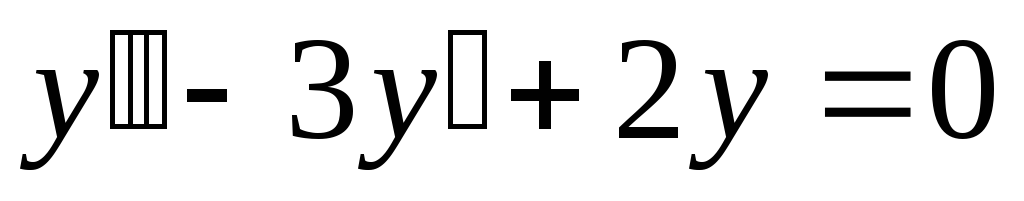 ;
б).
;
б).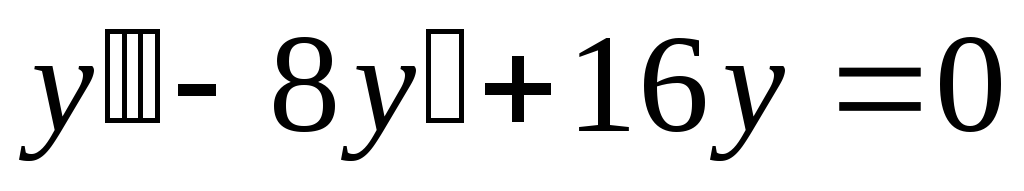 ;
в).
;
в).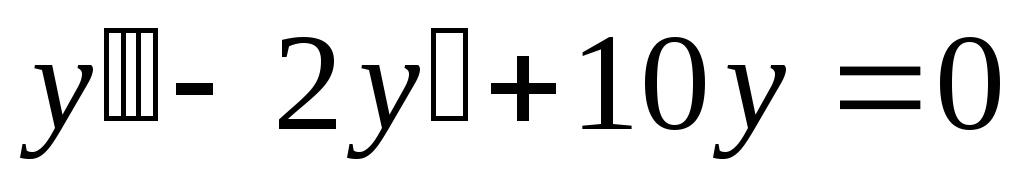 .
.а).
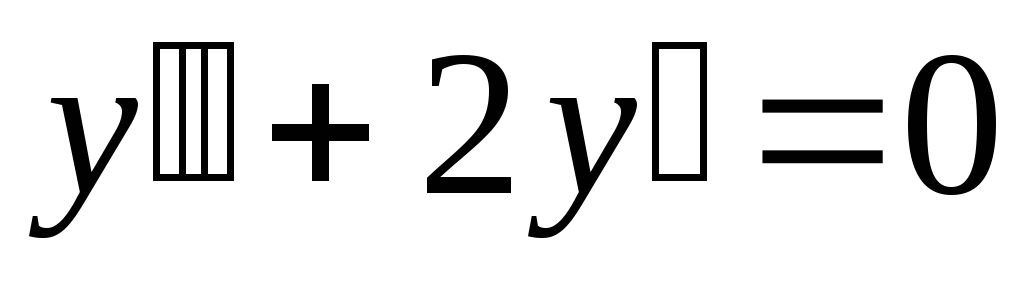 ;
б).
;
б).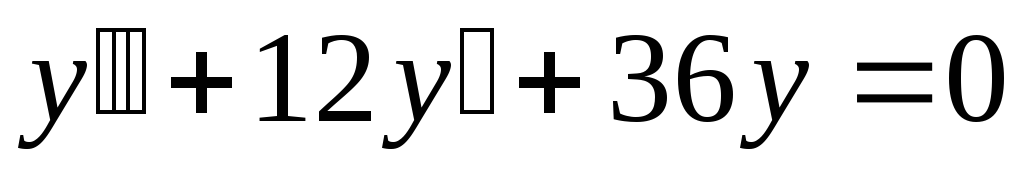 ;
в).
;
в).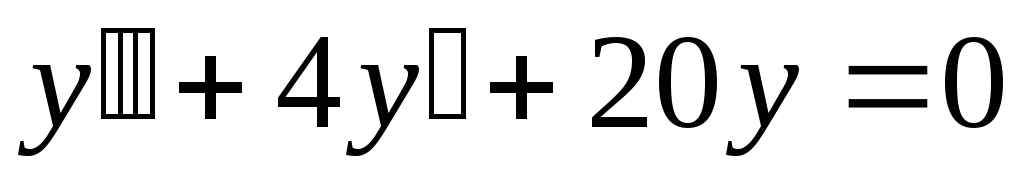 .
.а).
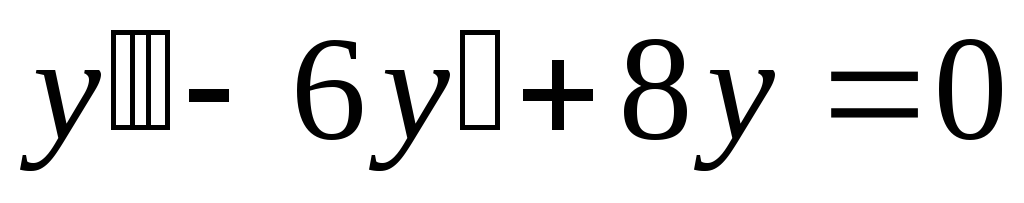 ;
б).
;
б).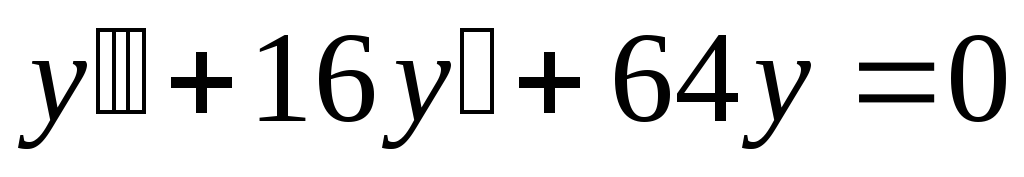 ;
в).
;
в).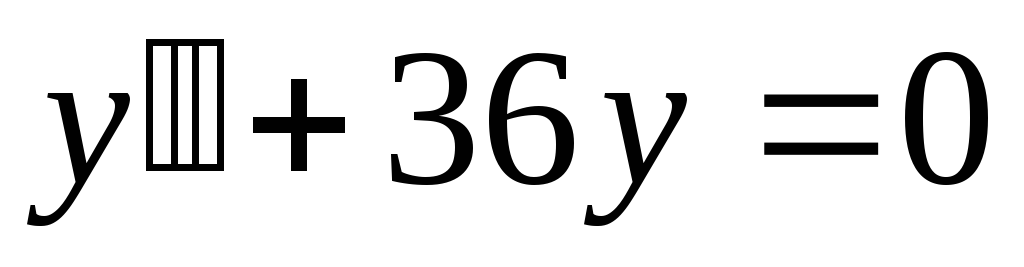 .
.а).
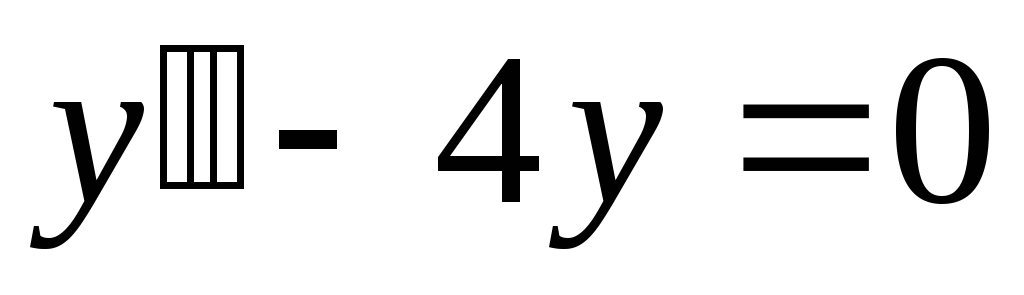 ;
б).
;
б).
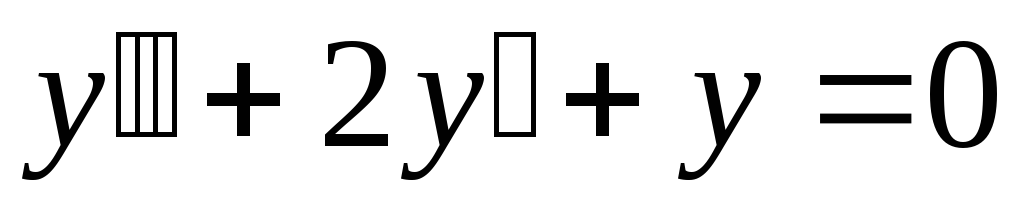 ;
в).
;
в).
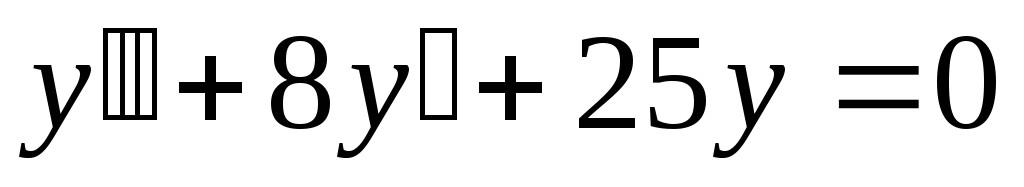 .
.
Пример.а).![]() .
.
Составим соответствующее характеристическое уравнение:
![]() ,
,
![]() ,
,
![]() .
.
Так как корни
характеристического уравнения
![]() действительные, различные, следовательно,
общее решение однородного уравнения
имеет вид
действительные, различные, следовательно,
общее решение однородного уравнения
имеет вид
![]() ,
то есть имеем
,
то есть имеем
![]() .
.
б).
![]() .
.
Составим соответствующее характеристическое уравнение:
![]() ,
,
![]() .
.
Так как корни
характеристического уравнения
![]() действительные, одинаковые, следовательно,
общее решение однородного уравнения
имеет вид
действительные, одинаковые, следовательно,
общее решение однородного уравнения
имеет вид
![]() ,
то есть имеем
,
то есть имеем
![]() .
.
в).
![]() .
.
Составим соответствующее характеристическое уравнение:
![]() .
Решим его при помощи вычисления
дискриминанта:
.
Решим его при помощи вычисления
дискриминанта:
![]() .
Так как в данном случае
.
Так как в данном случае
![]() ,
то для вычисления квадратного корня
,
то для вычисления квадратного корня![]() используем равенство
используем равенство![]() .
Так как
.
Так как![]() (комплексная единица), то в данном случае
(комплексная единица), то в данном случае![]() .
Таким образом, имеем в данном случаекомплексные
корни:
.
Таким образом, имеем в данном случаекомплексные
корни:
![]() .
.
Так как корни
характеристического уравнения
![]() комплексно-сопряженные,
следовательно, общее решение однородного
уравнения имеет вид
комплексно-сопряженные,
следовательно, общее решение однородного
уравнения имеет вид
![]() ,
где
,
где
![]() и
и
![]() - соответственно действительная и мнимая
части комплексных корней. В данном
случае
- соответственно действительная и мнимая
части комплексных корней. В данном
случае
![]() .
Таким образом, общее решение исходного
уравнения имеет вид:
.
Таким образом, общее решение исходного
уравнения имеет вид:
![]() .
.
Ряды.
151
– 160.Исследовать сходимость числового
ряда![]() .
.
