5. Метод вариации постоянных для неоднородных уравнений и систем

Рассмотрим теперь неоднородные уравнения и системы. Мы покажем, что если известны решения однородной системы то для любой вектор-функцииможно получить решения неоднородной системыметодом вариации постоянныхтак же, как это делалось для линейного неоднородного уравнения первого порядка. Аналогично этому, зная общее решение однородного уравненияп-го порядкаэтим методом можно получить все решения неоднородного уравнения

Пусть фундаментальная система решений однородной системыТогда общее решение однородной системы имеет видгдепостоянные. Будем искать решение неоднородной системы в виде

(10)

Продифференцируем это равенство: Потребуем, чтобы функцияудовлетворяла системеПолучим:

(11)

Так как решение однородной системы, топоэтому из равенства (11) после сокращения мы получим:Это векторное равенство можно переписать в виде системы линейных уравнений относительно

(11)

Определитель этой системы – это определитель Вронского Так какфундаментальная система решений, тоне равен нулю ни в одной точке отрезкаСледовательно, система (11) разрешима для любой точкиТаким образом, на всём отрезкесуществуют непрерывные функцииПосле нахождения этих функций функцииможно будет найти простым интегрированием. Подставив найденные функциив формулу (10), мы получим решение неоднородной системы.

Замечание. Только что описанным способом будут получены все решения неоднородной системы, хотя достаточно найти хотя бы одно (частное) решение.

Опишем теперь метод вариации постоянных для неоднородных уравнений. Пусть дано уравнение

(12)

Предположим, что известна фундаментальная система решений однородного уравненияТогда общее решение однородного уравнения имеет видгдепостоянные. Будем искать решение неоднородного уравнения в виде

(13)

Найдём производную:

Потребуем выполнения условия

Таким образом, Продифференцируем ещё раз:Наложим условие

Будем далее дифференцировать и накладывать условия доПосле этого будем иметьПродифференцируем последний раз:Подставим в уравнение (12):

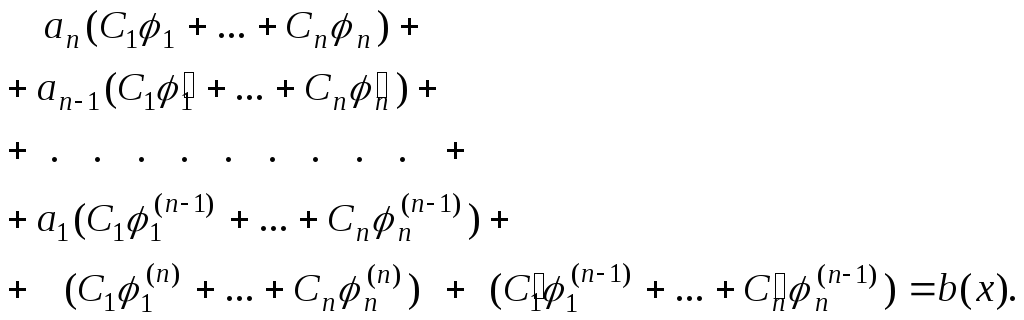
Так как решения однородной системы, то в левой части равенства сумма всех слагаемых сравна нулю, и мы получаем только слагаемые сследовательно,

Уравнения образуют систему линейных уравнений относительно

(15)

Определитель этой системы является определителем Вронского, а так как функцииобразуют фундаментальную систему решений, то(ни в одной точке отрезкаСледовательно, система (15) имеет решение, состоящее из функций непрерывных на отрезке Функциимогут быть теперь найдены интегрированием. Подставив полученные функциив формулу (13), мы получим решение неоднородного уравнения.

6. Однородные уравнения с постоянными коэффициентами

Рассмотрим теперь линейное однородное уравнение с постоянными коэффициентами

(16)

где постоянные числа. Мы покажем, что нахождение фундаментальной системы решений этого уравнения фактически сводится к решению алгебраического уравненияп-й степени (квадратного при кубического при и т.д.).

Найдём вначале все решения этого уравнения, имеющие вид гдеНайдём производные этой функции:Подставим их в уравнение (16):

После сокращения на получимхарактеристическое уравнение

(17)

Предположим, что имеет место “самый хороший” случай: корни характеристического уравнения действительны и различны. Тогда уравнение можно считать решённым: действительно, в этом случае мы имеем п линейно независимых функций являющихся решениями уравнения (16), а это означает, что фундаментальная система решений этого уравнения. Следовательно, общее решение уравнения имеет вид

где произвольные константы.

Например, если дано уравнение то, полагаяполучим:откудаилиМы имеем две линейно независимые функциииудовлетворяющие уравнению, поэтому общее решение уравнения имеет вид

Если характеристическое уравнение имеет кратный корень R, то, как будет показано ниже, решениями этого уравнения, наряду с функцией решениями этого уравнения будут также функциигдекратность корняДокажем это.

Лемма. Пусть корень характеристического уравнения (17) икратность этого корня. Тогда функцииудовлетворяют уравнению (16).

Доказательство. Уравнение (16) запишем в виде гдеаТак каккорень кратностито многочленделится нат.е.гдетакже многочлен отВыясним, как действует операторна функциюИмеем:

и т.д. Ясно, что приВ частности,приа значит,Это показывает, что функцияявляется решением уравнения (16). Лемма доказана.

Рассмотрим пример применения этой теоремы. Пусть дано уравнение Составим характеристическое уравнение:Разлагая левую часть на множители, получим:ОтсюдаПростой кореньдаёт функциюа двукратный кореньдве функции:иТаким образом,общее решение уравнения.

Завершим разбор ситуации, когда корни характеристического уравнения все являются действительными числами. Пусть корень кратностикратностикратностиТогдаСуммаявляется степенью многочленапоэтомугдепорядок данного уравнения. Функции

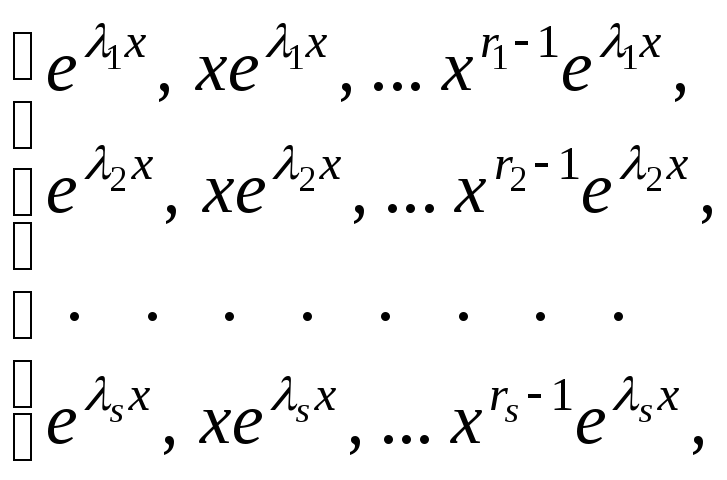(18)

очевидно, линейно независимы и являются (ввиду леммы) решениями уравнения (16). Так как количество этих функций равно то (18) – фундаментальная система решений уравнения

Перейдём теперь к рассмотрению случая, когда характеристическое уравнение имеет комплексные корни. Пустькомплексный корень этого уравнения. Функция– комплекснозначная функция действительного аргумента – является, очевидно, комплексным решением уравнения (16), но нам требуется найтидействительные решения. Преобразуем эту функцию. Имеем: гдеПроверим, что эти функцииисами являются решениями уравнения (16). Действительно, так кактоВвиду того, чтомногочлен с действительными коэффициентами, мы получаем:

В случае, когда комплексный корень кратностианалогичные рассуждения показывают, что функцииудовлетворяют уравнению (16). Таким образом, комплексный корень кратностидаётлинейно независимых решений уравнения (16). Причина того, что количество получаемых решений вдвое больше кратности корня состоит в том, что для числаи сопряжённого числа (которое обязательно тоже будет корнем характеристического уравнения) набор функций один и тот же.

Теперь рассмотрены все случаи, которые могут представиться при решении характеристического уравнения, и мы получаем теорему.

Теорема. Фундаментальная система решений уравнения -го порядкас постоянными коэффициентами имеет ровнолинейно независимых решений, причём:

а) действительный корень кратности даёт решения

б) комплексный корень кратностиR) даёт решения ...

Проиллюстрируем теорему одним примером, а именно, найдём все решения уравнения Составим характеристическое уравнение:Его корни:Комплексными решениями уравнения являются функциииа их действительные и мнимые частиобразуют фундаментальную систему решений. Таким образом, общее решение уравнения имеет видгдепроизвольные действительные константы.

В заключение этого параграфа разберём метод решения одного типа уравнений, сводящихся к уравнениям с постоянными коэффициентами. Однородным уравнением Эйлера называется уравнение вида

(19)

где действительные константы. Для решения этого уравнения введём новую независимую переменную полагая Производные функциипонадо теперь выразить через производныепоИмеем:

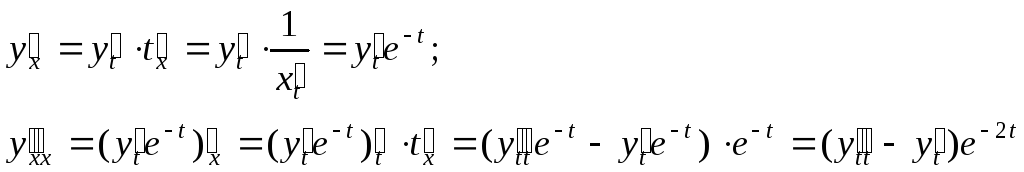
и т.д. Подставив эти выражения в уравнение (19), мы получим уравнение с постоянными коэффициентами. Заметим, что в области заменанезаконна, но в этом случае можно сделать заменуи уравнение (19) также сведётся к уравнению с постоянными коэффициентами.