
Задачи для самостоятельного решения
Сколько компонент связности имеет граф со следующим набором степеней вершин: 1, 1, 1, 2, 2, 2, 2, 3?
Изобразить граф
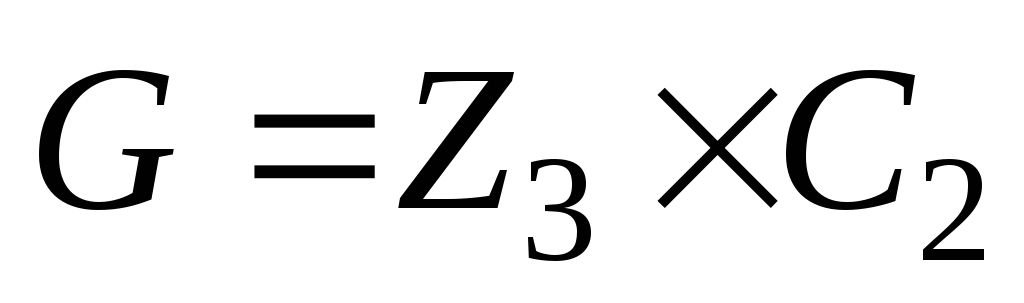 .
Найти
.
Найти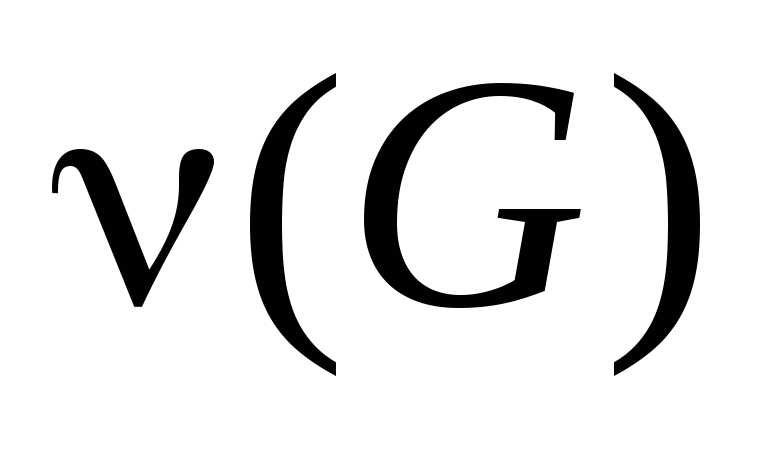 ,
построить базис циклов.
,
построить базис циклов.Изобразить граф
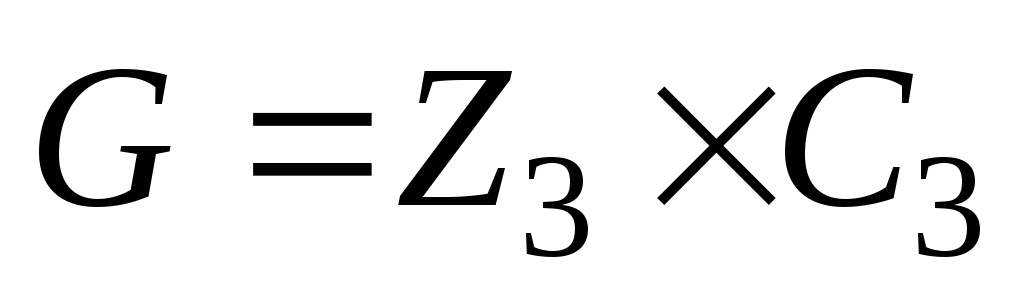 .
Найти
.
Найти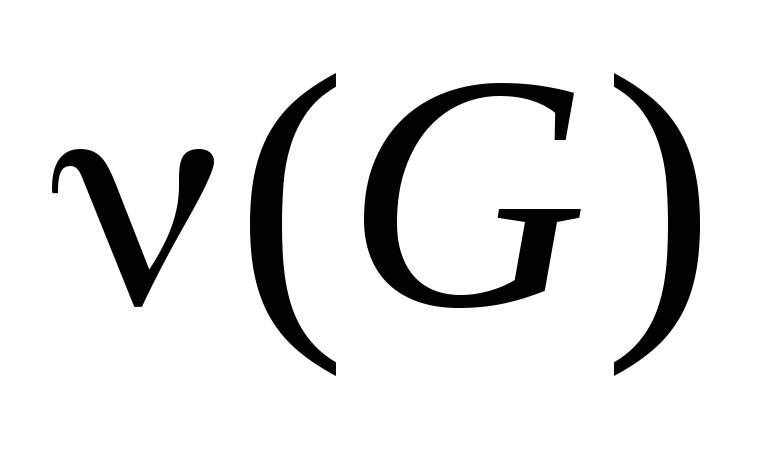 ,
построить базис циклов.
,
построить базис циклов.Построить базис циклов графа
 .
.Построить базис циклов графа
 .
.Построить базис циклов графа
 .
.Построить базис циклов графа
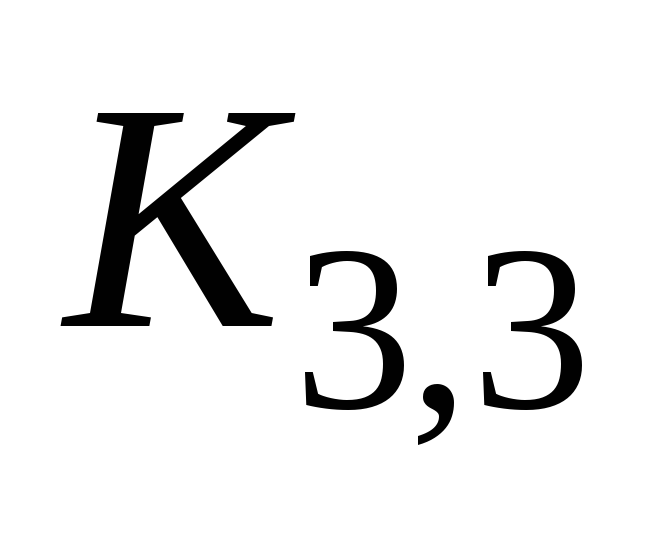 .
.Является ли деревом прямое произведение деревьев?
Найти число компонент связности леса, который имеет 76 вершин и 53 ребра.
Сколько ребер имеет лес с 10 вершинами, если он имеет 3 компоненты связности?
Чему может равняться число компонент связности графа, имеющего 15 вершин и 35 ребер?
Чему может равняться число компонент связности графа, имеющего 12 вершин и 20 ребер?
Чему может равняться число ребер графа, имеющего 10 вершин и 3 компоненты связности?
Доказать, что если граф имеет 10 вершин и 37 ребер, то он связен.
Доказать, что если граф имеет 8 вершин и 23 ребра, то он связен.
Связный граф имеет 12 вершин. Сколько он может иметь ребер?
Сколько ребер может быть у связного графа с пвершинами?
Сколько всего неизоморфных деревьев с пятью вершинами? Изобразить их.
Сколько всего графов с 12 вершинами и 65 ребрами? с 64 ребрами?
Построить коды деревьев (два для каждого дерева), изображенных на рис. 2.43.
Построить дерево по коду (00101001011101).
Построить дерево по коду (00101011001101).
Построить дерево по коду [5345566].
Построить дерево по коду [4445477].
У
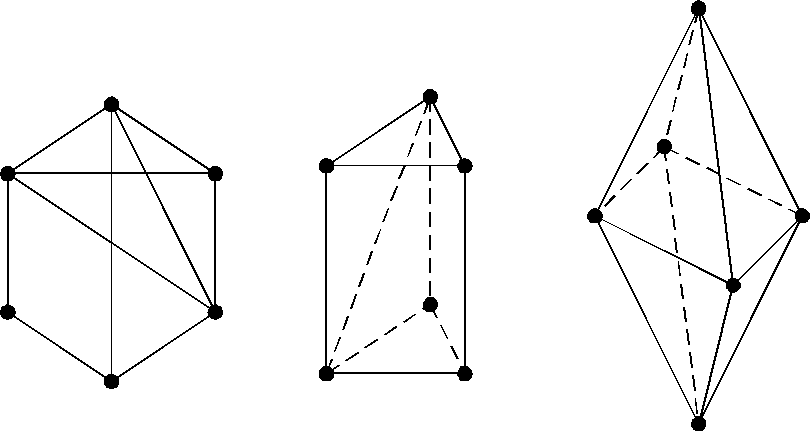
а) б) в)
Рис. 2.44
каких из графов, изображенных на рис. 2.44, существует эйлеров путь или эйлеров цикл? Если существует, то построить его.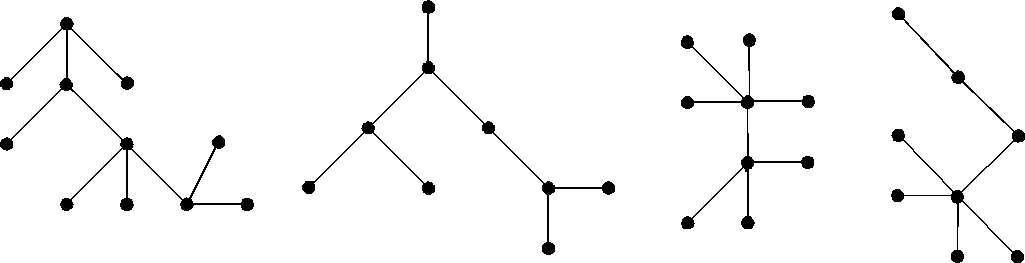
а) б) в) г)
Рис. 2.43
Ответы
1.
1 или 2.Указание.Рассмотреть,
сколько вершин может быть в каждой
компоненте связности.2.См. рис. 2.45.![]() .
Базис циклов: (1, 2, 3), (1, 3, 6, 4), (3, 2, 5, 6), (1,
2, 5, 4).3.
.
Базис циклов: (1, 2, 3), (1, 3, 6, 4), (3, 2, 5, 6), (1,
2, 5, 4).3.![]() .4.
.4.![]() .
.
5.
![]() .6.
.6.![]() .7.
.7.![]() .8. Не
является (см. рис. 2.12).
.8. Не
является (см. рис. 2.12).
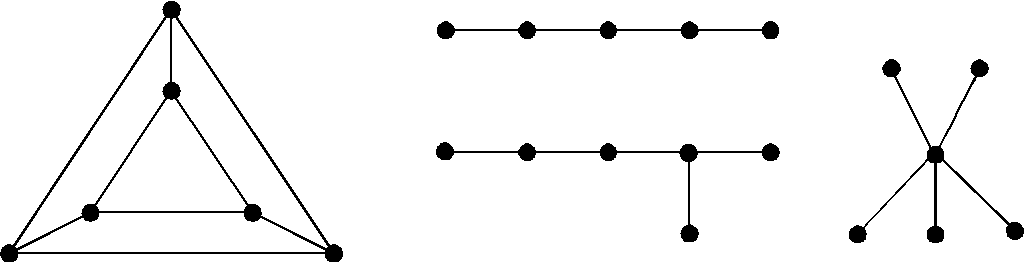
Рис. 2.45 Рис. 2.46
9.
23. 10.
7.11. От
1 до 7.12.
От 1 до 6.13.
От 7 до 28.14. Указание.Доказать,
что несвязный граф с 10 вершинами имеет
не более 36 ребер.15.
Указание. Доказать, что несвязный
граф с 8 вершинами имеет не более 21 ребра.16. От
11 до 66.17.
От![]() до
до![]() .18.3 , см
рис. 2.46.Указание.Рассмотреть
возможные наборы степеней вершин.19.
Один, два.20.
При нумерации, указанной на рис. 2.47:
.18.3 , см
рис. 2.46.Указание.Рассмотреть
возможные наборы степеней вершин.19.
Один, два.20.
При нумерации, указанной на рис. 2.47:
а)(01000010110101101101), [114457557];б)(0000101110010111); [2332477];в)(0010100101011011), [ 4444666];
г)(00001010101111), [246666].21. См. рис. 2.48а .22. См. рис. 2.48б.
2
Рис. 2.47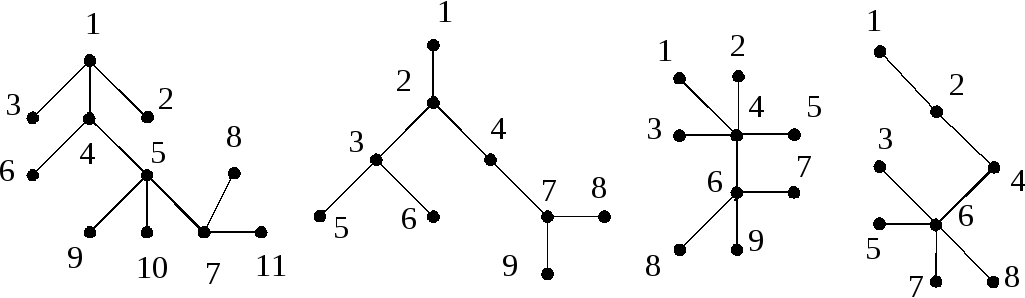
А) б) в) г)
а) б) в)
г)
Рис. 2.48
