
Литература / Прокофьевская книга по дискретке / glava2-4
.DOC§2.4. Раскраски графов. Планарность
Пусть
задано несколько красок
![]() .
Раскраской графа G называется
правило, по которому каждой вершине
графа присваивается номер
.
Раскраской графа G называется
правило, по которому каждой вершине
графа присваивается номер
![]() ,
соответствующий краске, причем смежные
вершины имеют разные номера.
,
соответствующий краске, причем смежные
вершины имеют разные номера.
Хроматическим
числом
![]() графа G называется наименьшее
число красок, требуемое для раскраски
данного графа.
графа G называется наименьшее
число красок, требуемое для раскраски
данного графа.
Для
полного графа
![]() .
.
Граф
называется бихроматичным, если
для его раскраски требуется две краски
(![]() ).
).
Теорема (Критерий бихроматичности). Для любого графа G эквивалентны условия:
-
граф G бихроматичен;
-
граф G двудольный;
-
в графе G нет циклов нечетной длины.
Доказательство.
Будем доказывать эквивалентность по
схеме
![]() .
.
![]() Пусть граф G
бихроматичен. Нужно доказать, что в нем
нет циклов нечетной длины. Предположим,
что цикл нечетной длины существует:
Пусть граф G
бихроматичен. Нужно доказать, что в нем
нет циклов нечетной длины. Предположим,
что цикл нечетной длины существует:
![]() .
В силу бихроматичности нечетные вершины
одного цвета. Следовательно, вершины
.
В силу бихроматичности нечетные вершины
одного цвета. Следовательно, вершины
![]() и
и
![]() одного
цвета, но они смежные. Получили
противоречие. Циклов нечетной длины
нет.
одного
цвета, но они смежные. Получили
противоречие. Циклов нечетной длины
нет.
![]() Пусть в графе G
нет циклов нечетной длины. Нужно доказать,
что G двудольный. Пусть
Пусть в графе G
нет циклов нечетной длины. Нужно доказать,
что G двудольный. Пусть
![]() –
компоненты связности графа G.
Достаточно доказать, что каждая компонента
связности является двудольным графом.
Поэтому можно считать G связным
графом, т.е. любые две вершины в нем
соединены путем. Введем на множестве
вершин графа V отношение “~”
следующим образом:
–
компоненты связности графа G.
Достаточно доказать, что каждая компонента
связности является двудольным графом.
Поэтому можно считать G связным
графом, т.е. любые две вершины в нем
соединены путем. Введем на множестве
вершин графа V отношение “~”
следующим образом:![]() ,
если существует путь четной длины из
вершины
,
если существует путь четной длины из
вершины
![]() в вершину
в вершину
![]() .
Если из
.
Если из
![]() в
в
![]() существует
путь четной длины, то из
существует
путь четной длины, то из
![]() в
в
![]() не существует пути нечетной длины, иначе
нашелся бы цикл нечетной длины.
не существует пути нечетной длины, иначе
нашелся бы цикл нечетной длины.
Докажем,
что “~” – отношение эквивалентности.
Действительно, оно рефлексивно:
![]() (из
(из
![]() в
в
![]() существует путь длины 0); симметрично:
если
существует путь длины 0); симметрично:
если
![]() ,
то
,
то
![]() (если из
(если из
![]() в
в
![]() существует
путь четной длины, то существует путь
четной длины из
существует
путь четной длины, то существует путь
четной длины из
![]() в
в
![]() );
транзитивно: если
);
транзитивно: если
![]() и
и
![]() ,
то
,
то
![]() (если существует пути четной длины из
(если существует пути четной длины из
![]() в
в
![]() и из
и из
![]() в
в
![]() ,
то существует пути четной длины из
,
то существует пути четной длины из
![]() в
в
![]() .
Следовательно, множество вершин графа
V разбивается на два класса
эквивалентности V1 и V2
: V1 – множество вершин графа,
до которых из фиксированной вершины а
существует путь четной длины, V2
– множество вершин графа, до которых
из фиксированной вершины а существует
путь нечетной длины. Тогда концы
произвольного ребра лежат в разных
множествах V1 и V2,
иначе для двух вершин одного множества
существовал бы путь длины 1 по этому
ребру. Следовательно, граф G
двудольный.
.
Следовательно, множество вершин графа
V разбивается на два класса
эквивалентности V1 и V2
: V1 – множество вершин графа,
до которых из фиксированной вершины а
существует путь четной длины, V2
– множество вершин графа, до которых
из фиксированной вершины а существует
путь нечетной длины. Тогда концы
произвольного ребра лежат в разных
множествах V1 и V2,
иначе для двух вершин одного множества
существовал бы путь длины 1 по этому
ребру. Следовательно, граф G
двудольный.
![]() Пусть G –
двудольный граф. Нужно доказать, что он
бихроматичен. Так как смежные вершины
графа принадлежат разным долям, то
вершины одной доли раскрасим в один
цвет, второй – в другой. Теорема доказана.
Пусть G –
двудольный граф. Нужно доказать, что он
бихроматичен. Так как смежные вершины
графа принадлежат разным долям, то
вершины одной доли раскрасим в один
цвет, второй – в другой. Теорема доказана.
Реберным
хроматическим числом
![]() графа G называется наименьшее
количество красок, необходимых для
раскраски ребер графа таким образом,
чтобы смежные ребра имели разные цвета.
графа G называется наименьшее
количество красок, необходимых для
раскраски ребер графа таким образом,
чтобы смежные ребра имели разные цвета.
Для
полных графов
![]()
Если
![]() то, очевидно,
то, очевидно,
![]() .
.
Справедлива
теорема Визинга.
![]() .
.
Планарные графы
Граф G называется планарным, если его можно изобразить на плоскости без пересечения ребер.
П
Рис. 2.49
Рис. 2.50

П
Рис.
2.53
Рис. 2.51
Рис. 2.52

Теорема
(Эйлера). В любом планарном связном
графе![]() ,
где
,
где
![]() –
количество вершин,
–
количество вершин,
![]() –
граней,
–
граней,
![]() –
ребер.
–
ребер.
Доказательство.
проведем индукцией по числу ребер.
При
![]()
![]() ,
,
![]() (океан),
и равенство
(океан),
и равенство
![]() выполняется.
выполняется.
П
Рис. 2.54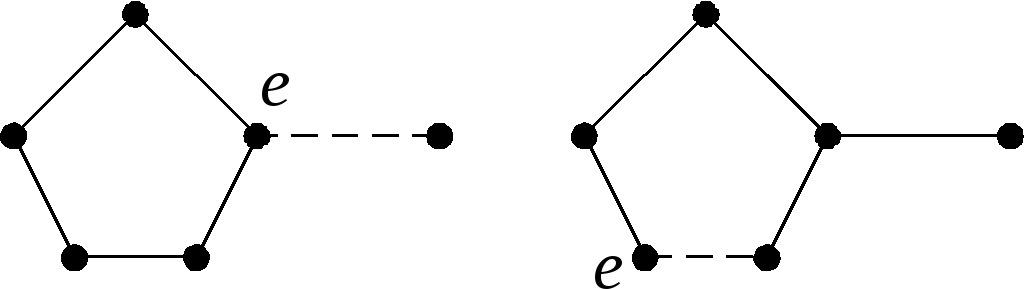
![]() .
Возьмем произвольно ребро е графа
G, и удалим его, если оно висячее, то
вместе с соответствующей вершиной. Если
ребро было висячим, то для нового графа
G' имеем
.
Возьмем произвольно ребро е графа
G, и удалим его, если оно висячее, то
вместе с соответствующей вершиной. Если
ребро было висячим, то для нового графа
G' имеем
![]() ,
,
![]() ,
,
![]() (рис. 2.54а). Так как число ребер у G'
меньше, чем у G, то по индукционному
предположению
(рис. 2.54а). Так как число ребер у G'
меньше, чем у G, то по индукционному
предположению
![]() и, следовательно,
и, следовательно,
![]() .
.
Если
было удалено невисячее ребро (рис.
2.54б), то
![]() ,
,
![]() ,
,
![]() .
Аналогично,
.
Аналогично,
![]() и, следовательно,
и, следовательно,
![]() .
Теорема доказана.
.
Теорема доказана.
Пусть
G – планарный граф. Если у него есть
висячие ребра, то добавим произвольные
ребра, чтобы висячих не осталось. При
этом хроматическое число
![]() может
только увеличится. Граф без висячих
вершин будем называть замкнутым.
Далее рассматриваются планарные
графы без петель, но в которых могут
быть кратные ребра.
может
только увеличится. Граф без висячих
вершин будем называть замкнутым.
Далее рассматриваются планарные
графы без петель, но в которых могут
быть кратные ребра.
Пусть G – планарный граф. Построим граф G* следующим образом. Число вершин графа G* равно числу граней G. Каждой грани G поставим в соответствие вершину G*. Вершины в G* смежны тогда и только тогда, когда соответствующие им грани в G граничат по ребру, причем две вершины G* соединяет столько ребер, сколько общих граничных ребер у соответствующих им граней. Граф G* называется двойственным (сопряженным) графу G.
В
а)
б)
Рис. 2.55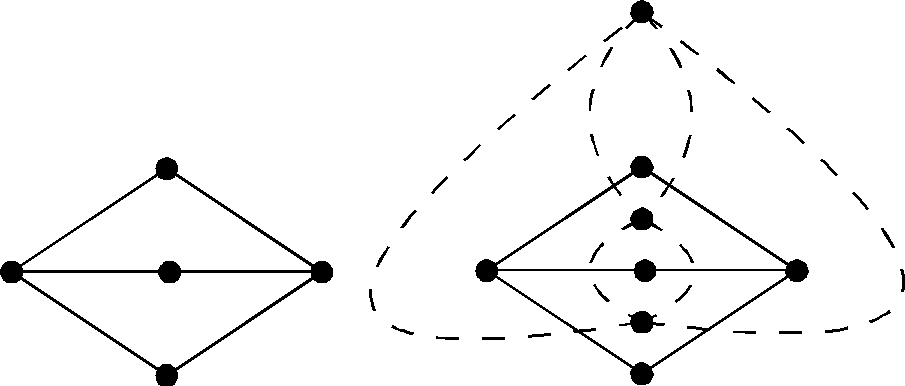
![]() ,
соединим ребрами
,
соединим ребрами
![]() ,
пересекающими
,
пересекающими
![]() .
Ребра
.
Ребра
![]() графа
G и
графа
G и
![]() графа G* ,
графа G* ,
![]() ,
называются перпендикулярными
(рис. 2.55б).
,
называются перпендикулярными
(рис. 2.55б).
При
этом внутри каждой грани графа G*
лежит единственная вершина графа G.
Действительно, предположим, что внутри
некоторой грани
![]() графа G* находятся несколько вершин
графа G* находятся несколько вершин
![]() графа G. Так как из каждой вершины
выходит по крайней мере одно ребро, а
каждое ребро
графа G. Так как из каждой вершины
выходит по крайней мере одно ребро, а
каждое ребро
![]() пересекает ровно одно ребро графа G,
то
пересекает ровно одно ребро графа G,
то
![]() ,
где п – число ребер грани
,
где п – число ребер грани
![]() .
Тогда, если какие-либо две из вершин
соединены ребром, то внутри грани
.
Тогда, если какие-либо две из вершин
соединены ребром, то внутри грани
![]() найдется ребро
найдется ребро
![]() ,
пересекающее это ребро, чего быть не
может, так как внутри грани ребер нет.
Пусть никакие две из вершин графа G,
находящиеся внутри
,
пересекающее это ребро, чего быть не
может, так как внутри грани ребер нет.
Пусть никакие две из вершин графа G,
находящиеся внутри
![]() ,
не соединены ребром. Тогда все ребра,
выходящие из этих вершин, пересекают
ребра грани
,
не соединены ребром. Тогда все ребра,
выходящие из этих вершин, пересекают
ребра грани
![]() .
Так как каждое ребро графа
.
Так как каждое ребро графа
![]() пересекает ровно одно ребро графа G,
то
пересекает ровно одно ребро графа G,
то
![]() ,
где п – количество ребер и,
соответственно, вершин грани
,
где п – количество ребер и,
соответственно, вершин грани
![]() .
Проведение первого ребра из каждой
вершины не меняет число компонент
связности плоской области, ограниченной
гранью, проведение каждого следующего,
начиная со второго увеличивает число
компонент связности на 1. Таким образом,
в результате проведения всех ребер из
вершин
.
Проведение первого ребра из каждой
вершины не меняет число компонент
связности плоской области, ограниченной
гранью, проведение каждого следующего,
начиная со второго увеличивает число
компонент связности на 1. Таким образом,
в результате проведения всех ребер из
вершин
![]() ,
число компонент связности области,
ограниченной гранью, не превышает
,
число компонент связности области,
ограниченной гранью, не превышает
![]() .
Так как количество вершин грани
.
Так как количество вершин грани
![]() равно п, то найдутся две вершины,
лежащие в одной компоненте связности.
Но тогда они принадлежат одной грани
графа G, что противоречит определению
сопряженного графа.
равно п, то найдутся две вершины,
лежащие в одной компоненте связности.
Но тогда они принадлежат одной грани
графа G, что противоречит определению
сопряженного графа.
Таким образом, существует взаимно-однозначное соответствие между гранями G и вершинами G*, вершинами G и гранями G*, ребрами G и G*.
Теорема Эйлера (о пяти красках). Хроматическое число планарного графа не превосходит 5.
Доказательство.
Достаточно рассмотреть только
замкнутые графы, так как из всякого
незамкнутого графа можно получить
замкнутый добавлением ребра, что не
уменьшает хроматического числа. Пусть
G – планарный граф, G* – сопряженный
ему. Тогда
![]() .
Тогда вместо вершин можно раскрашивать
грани.
.
Тогда вместо вершин можно раскрашивать
грани.
Докажем теорему сначала для графов, степени всех вершин которых равны 3. Предварительно докажем лемму.
Лемма.
Пусть G – граф, у
которого
![]() для любой вершины
для любой вершины
![]() .
Тогда в нем существует грань, в которой
не больше 5 ребер. Пусть
.
Тогда в нем существует грань, в которой
не больше 5 ребер. Пусть
![]() –
количество k-угольных
граней в G ,
–
количество k-угольных
граней в G ,
![]() .
Тогда
.
Тогда
![]() –
количество ребер в k-угольных
гранях. В сумме
–
количество ребер в k-угольных
гранях. В сумме
![]() каждое
ребро считается ровно два раза, поэтому
каждое
ребро считается ровно два раза, поэтому
![]() .
Так как степени всех вершин равны 3,
имеем
.
Так как степени всех вершин равны 3,
имеем
![]() .
Воспользовавшись формулой
.
Воспользовавшись формулой
![]() ,
получим
,
получим
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Если
в графе нет двух-, трех-, четырех-,
пятиугольников, то
![]() и
и
![]() .
Получили противоречие, следовательно,
в графе есть хотя бы один из двух-, трех-,
четырех-, пятиугольников. Лемма доказана.
.
Получили противоречие, следовательно,
в графе есть хотя бы один из двух-, трех-,
четырех-, пятиугольников. Лемма доказана.
Доказательство теоремы для случая, когда степени всех вершин равны 3, проведем индукцией по числу граней графа. Предположим, что для всех графов с числом граней, меньшим п, утверждение верно и докажем для графа с п гранями. По лемме, в графе есть хотя бы один из двух-, трех-, четырех-, пятиугольников.
1) Есть двухугольник (рис. 2.56а). Объединим его с одной из соседних граней. Для нового графа (рис. 2.56б) по индукционному предположению существует раскраска пятью красками. Возвращаясь к исходному графу, раскрашиваем двухугольник в цвет, отличный от цвета двух соседних с ним граней.
2
а) б)
а) б)
Рис. 2.56
Рис. 2.57
Рис. 2.56
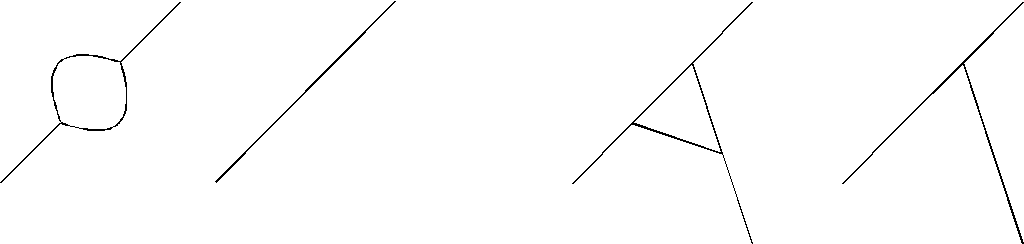
3
а) б)
Рис. 2.58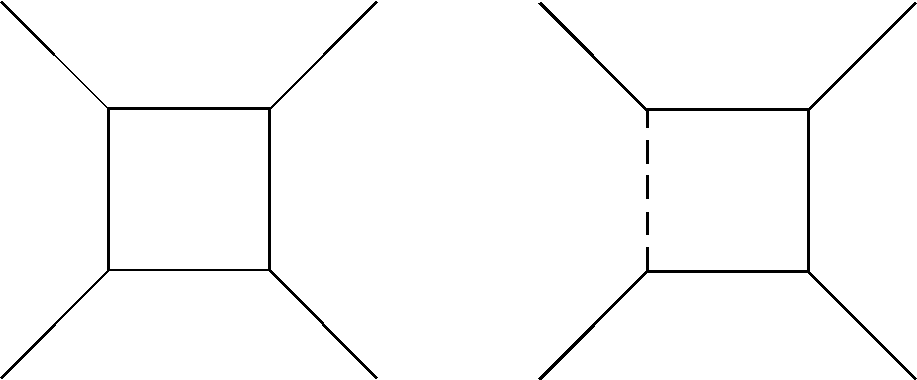
4
а)
б) в)
Рис. 2.59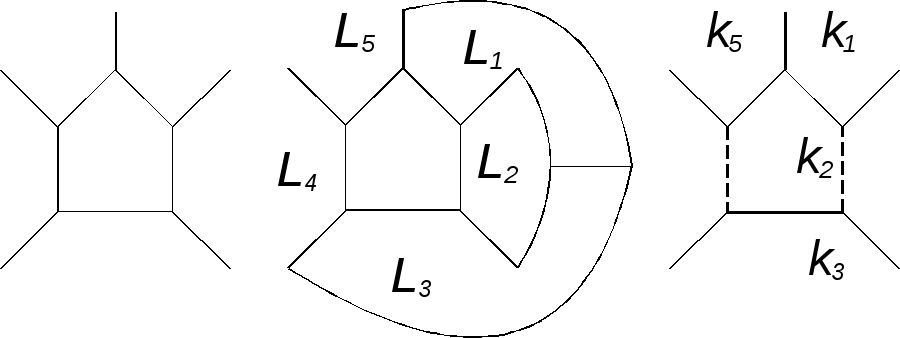
Объединим пятиугольник с гранями L2 и L4. Для нового графа (рис. 2.52в) по индукционному предположению существует раскраска пятью красками. Возвращаясь к исходному графу, раскрашиваем L2 и L4 тем цветом, который был у объединенной грани, пятиугольник в оставшийся пятый цвет. Теорема доказана для графа, у которого степени всех вершин равны 3 .
П
Рис. 2.60
Рис. 2.61
Теорема полностью доказана.
Рассмотрим теперь проблему планарности графов.
Теорема. Полный граф K5 не планарный.
Д
Рис. 2.62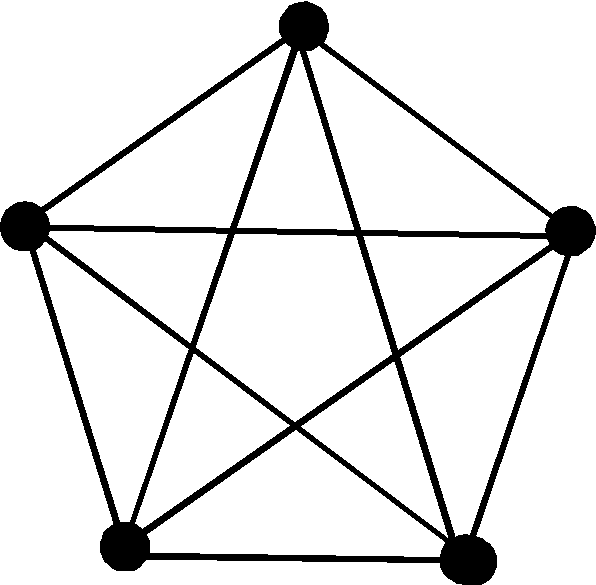
![]() .
Если бы он был планарный, то выполнялось
бы равенство
.
Если бы он был планарный, то выполнялось
бы равенство
![]() ,
т.е.
,
т.е.
![]() .
Двухугольные грани, очевидно, отсутствуют.
Имеем
.
Двухугольные грани, очевидно, отсутствуют.
Имеем
![]() .
Кроме того,
.
Кроме того,
![]() .
Умножим первое равенство на 3 и отнимем
из второго. Получим
.
Умножим первое равенство на 3 и отнимем
из второго. Получим
![]() .
Получили противоречие, следовательно,
граф K5 не планарный.
.
Получили противоречие, следовательно,
граф K5 не планарный.
Теорема. Полный двудольный граф K3,3 не планарный.
Д
Рис. 2.63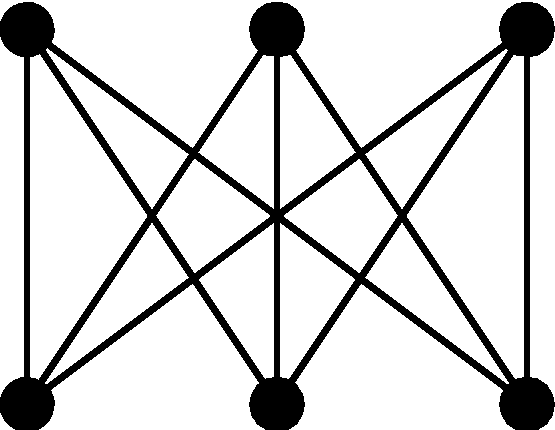
![]() .
Если бы он был планарный, то выполнялось
бы равенство
.
Если бы он был планарный, то выполнялось
бы равенство
![]() ,
т.е.
,
т.е.
![]() .
.
Имеем
![]() .
В силу того, что общее количество ребер
9, в графе не может быть граней с большим,
чем 9, числом ребер. Получаем
.
В силу того, что общее количество ребер
9, в графе не может быть граней с большим,
чем 9, числом ребер. Получаем
![]() ,
,![]() .
Так как граф K3,3
двудольный, то по
критерию бихроматичности в нем нет
циклов нечетной длины, следовательно,
нет граней с нечетным числом ребер:
.
Так как граф K3,3
двудольный, то по
критерию бихроматичности в нем нет
циклов нечетной длины, следовательно,
нет граней с нечетным числом ребер:
![]() .
Имеем
.
Имеем
![]() ,
,
![]() .
Умножив первое равенство на 4 и вычтя
его из второго, получим
.
Умножив первое равенство на 4 и вычтя
его из второго, получим
![]() .
Противоречие, граф K3,3
не планарный.
.
Противоречие, граф K3,3
не планарный.
П
Рис. 2.64
Рис. 2.65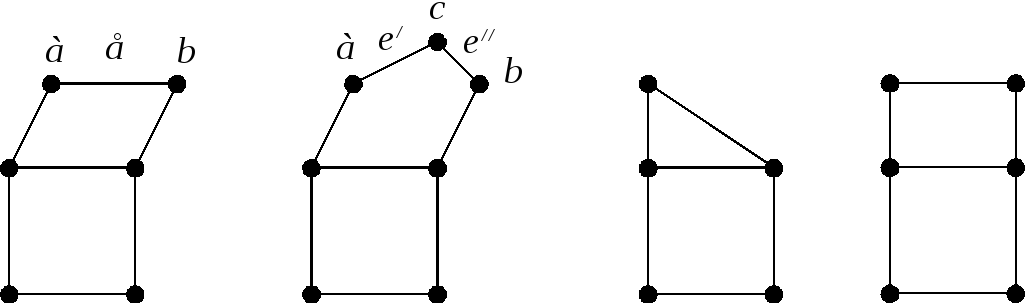
![]() и
и
![]() (рис. 2.64).
(рис. 2.64).
Графы G1 и G2 называются гомеоморфными, если существуют изоморфные графы G1' и G2', полученные из графов G1 и G2 применением один или несколько раз операции разбиения ребер.
Пример. Графы на рис. 2.65 не изоморфны, но гомеоморфны.
Если граф содержит непланарный подграф, то он сам не планарен.
Теорема (Критерий планарности А.С. Понтрягина – К. Куратовского). Граф G планарный тогда и только тогда, когда у него нет подграфов, гомеоморфных K5 или K3,3.
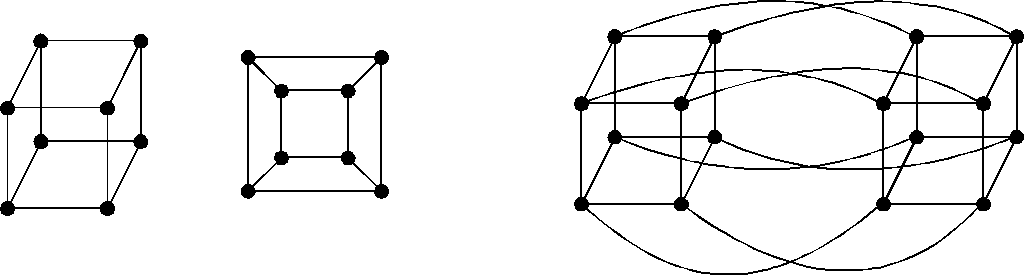
Пример. Доказать, что четырехмерный куб В4 не планарен.
Р
а)
б)
Рис. 2.66 X3 X4 X2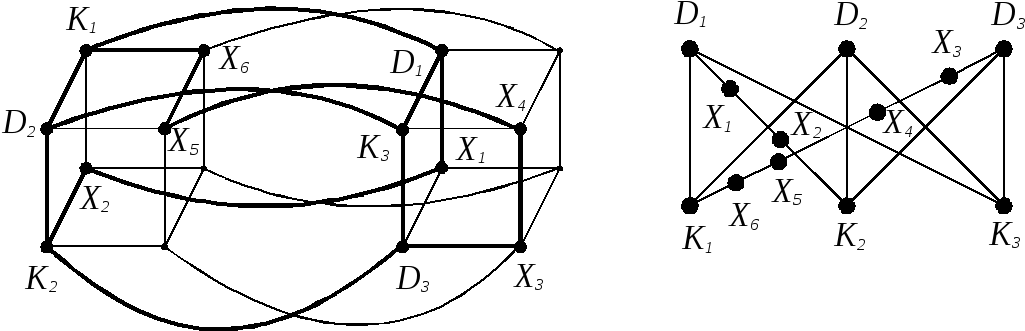
Задачи для самостоятельного решения
-
Является ли планарным граф
 ,
из которого удалено одно ребро?
,
из которого удалено одно ребро? -
Я
вляются ли планарными графы, изображенные на рис.2.67?
а) б) в) г)
Рис. 2.67
-
Является ли планарным граф, получающийся из
 добавлением главной диагонали (рис.
2.68а)?
добавлением главной диагонали (рис.
2.68а)? -
В
а) б) в)
Рис. 2.68
октаэдре соединены две противоположные вершины (рис. 2.68б). Является ли получившийся граф планарным? -
Планарен ли граф
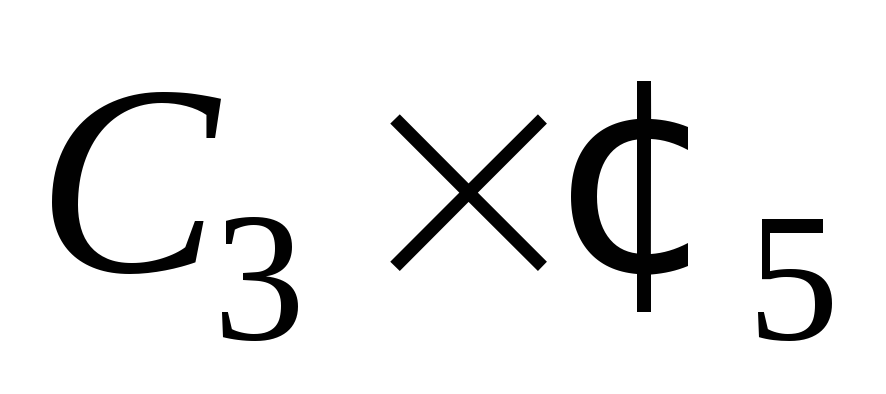 ?
? -
При каких значениях п 2 планарен граф (см. рис. 2.69)?
-
К
акое минимальное число ребер нужно удалить из графа
а) б)
Рис. 2.69
 ,
чтобы полученный граф стал планарным?
,
чтобы полученный граф стал планарным?
-
Какое минимальное число вершин нужно удалить из графа
 ,
чтобы полученный граф стал планарным?
,
чтобы полученный граф стал планарным? -
Найти хроматическое число графа
 .
. -
Найти реберное хроматическое число графа
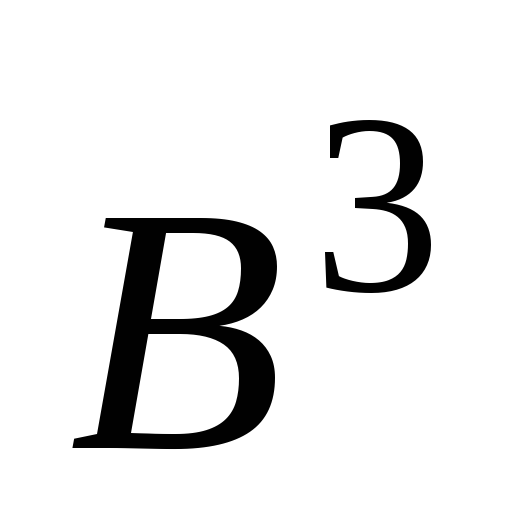 .
. -
Найти хроматическое число графа
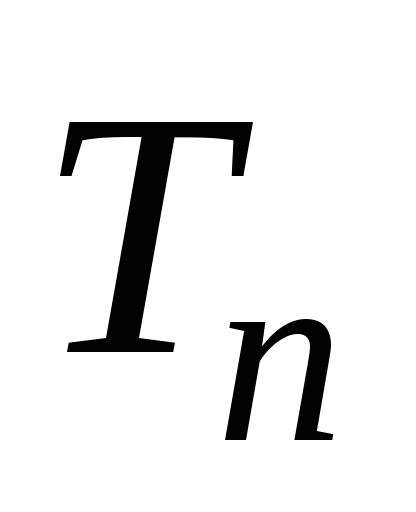 (дерева с п вершинами).
(дерева с п вершинами). -
Найти хроматическое число графа, изображенного на рис. 2.68в.
-
Привести пример плоского графа с хроматическим числом, равным 3.
-
Найти реберное хроматическое число графа
 .
. -
Найти хроматическое число и реберное хроматическое число графа
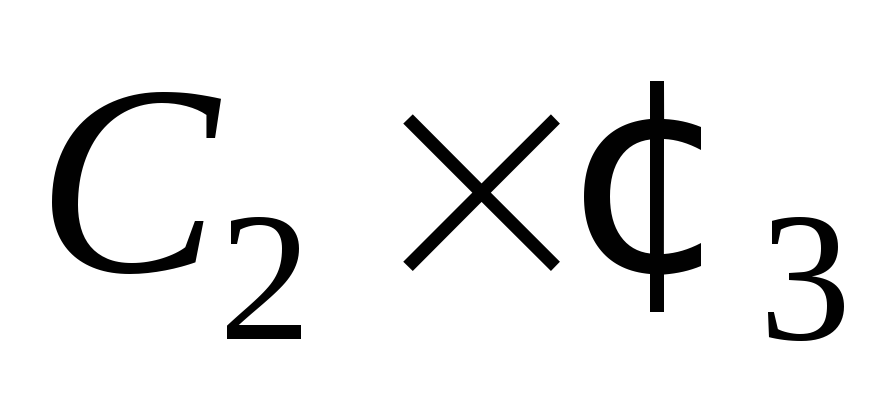 .
. -
Найти хроматическое число и реберное хроматическое число графа
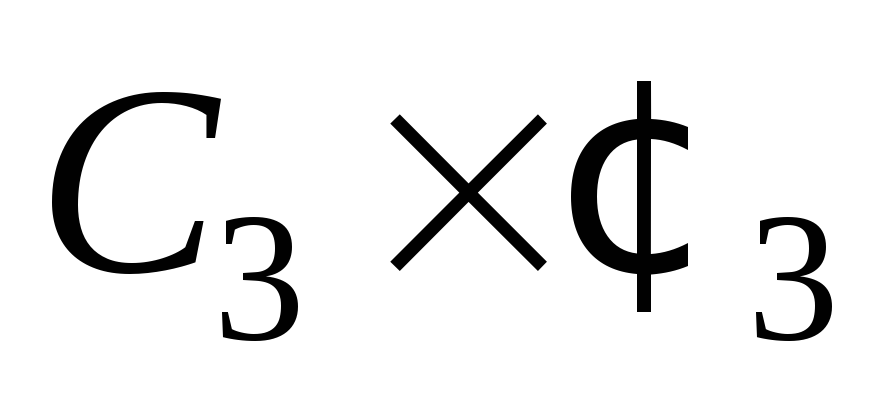 .
.
Ответы
1
Рис. 2.70
14.
5. Указание: учитывая, что
![]() ,
найти раскраску 5 красками.
,
найти раскраску 5 красками.
15. 3; 3. 16. 3; 4.
