Глава 3. Автоматы §3.1. Определение и примеры автоматов

Ф

Рис. 3.1

ункционирование автоматического устройства, работающего в дискретном режиме времени по заданному закону (определённому, например, схемой этого устройства), может быть описано на математическом языке с помощью понятияконечного автомата. В математической теории предполагается, что автоматимеет конечноемножество состоянийвходной алфавитвыходной алфавит причём в дискретные моменты временион принимает входной символизменяет (или сохраняет) своё состояние и выдаёт на выходе символИзменение (или сохранение) состояния и символна выходе автомата зависят от предыдущего состояния и принятого на входе символа

Обозначая через ивходной и выходной символы, соответствующие моменту временимы получим, что автоматперерабатывает входную последовательностьв выходную последовательность

Для построения математической теории конечных автоматов необходимо дать строгое определение этому понятию, его мы сейчас приведём.

Конечным автоматомназывается пятёркагдеконечные множества, аиотображения.

Отображение называетсяфункцией переходов, а отображениефункцией выходов. При этом равенствоозначает, что если автоматнаходится в данный момент времени в состояниии на его вход пришёл символа, то к следующему моменту времени он перейдёт в состояниеДалее, равенствоозначает, что если текущее состояние автомата естьа на вход поступил символа, то на выход будет послан символ

Работа автомата описывается системой канонических уравнений:

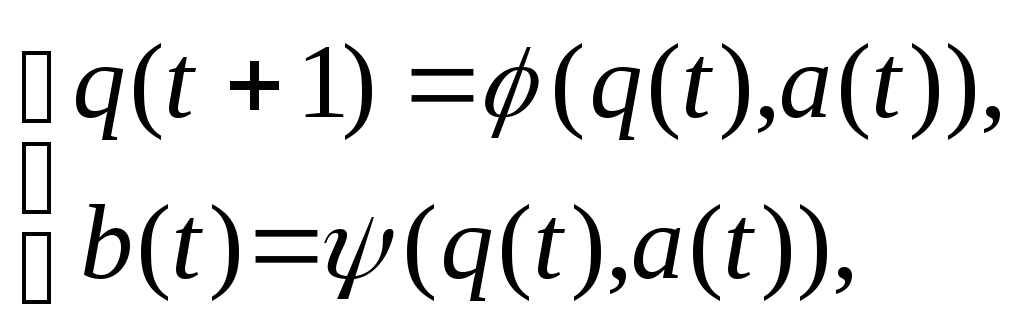
которая должна быть дополнена начальным условиемЗдесьначальное, илиинициальноесостояние.

Замечания.

1. Автомат в котором выделено начальное состояние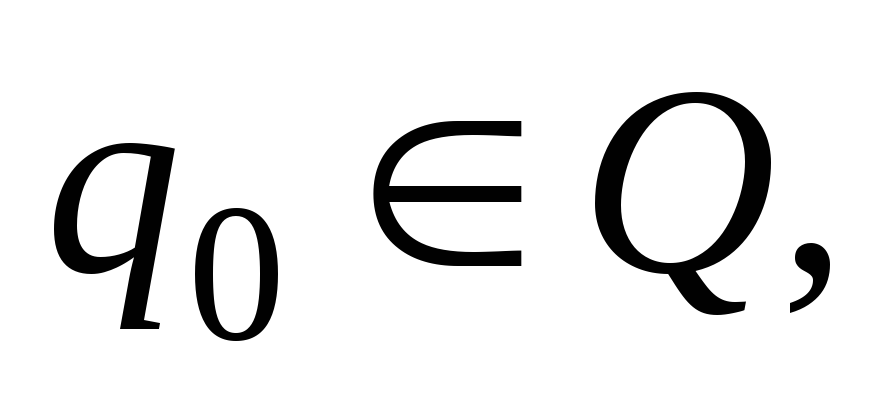иногда называютинициальным автоматом.

2. Иногда у автомата выделяют одно или несколько состояний (скажем,), называемыхконечными, илифинальнымисостояниями. Смысл их состоит в том, что если автомат “попадёт” в состоянието он прекращает свою работу.

3. Можно рассматривать вероятностные, илистохастическиеавтоматы, т.е. такие, в которых переход из одного состояния в другое и формирование выходного символа осуществляются не по жёстко заданному правилу, а с некоторой вероятностью, закон распределения которой должен быть указан. В отличие от вероятностных автоматов обычные автоматы называютдетерминированными.

4. Многие утверждения, касающиеся автоматов, справедливы и без предположения о том, что 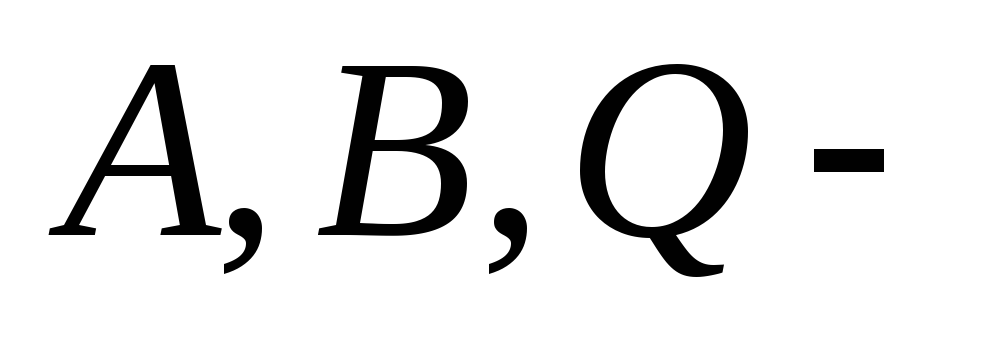конечные множества. Назовёмабстрактным автоматомпятёркугде функциииопределяются так же, как и раньше, т.е.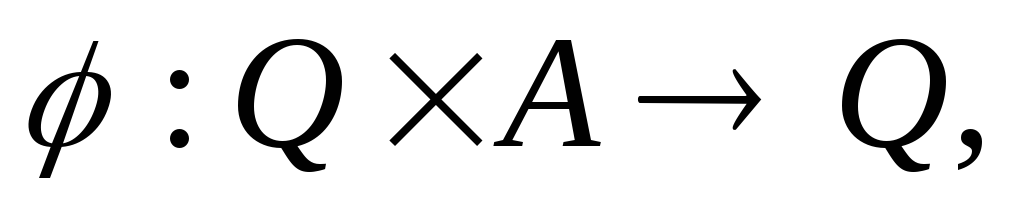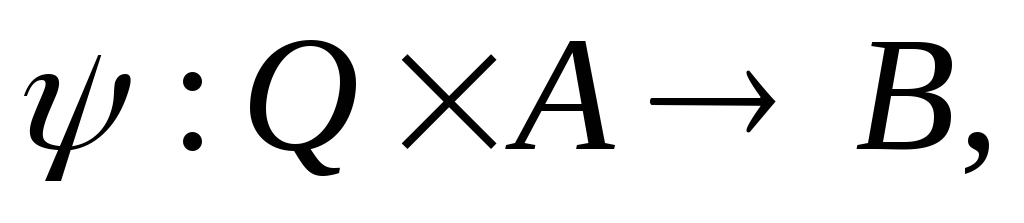но множествамогут быть бесконечными.

В теории автоматов рассматриваются вопросы исследования поведения автоматов, т.е. реакции автомата на то или иное внешнее воздействие (под которым здесь понимается слово или буква входного алфавита), вопросысинтеза автоматов(т.е. построения автоматов с теми или иными свойствами), а также некоторые другие вопросы.

Рассмотрим некоторые примеры автоматов.

П

Рис. 3.2. Элемент без памяти

ример 1.Автомат без памяти.Таким автоматом называется автомат, в котором множество состояний состоит в точности из одного элемента. В этом случае функциюможно не рассматривать, а функциязависит фактически только от пришедшей на вход автомата буквы входного алфавита. Канонические уравнения автомата выглядят здесь совсем просто:

Так, в частности, работает автомат, который осуществляет перекодировку символов одного алфавита в другой (если при этом одна буква заменяется на другую).

П

Рис. 3.3. Элемент задержки

ример 2.Элемент задержки.У этого автомата входной и выходной алфавиты совпадают:а выходной символ представляет собой задержанный на 1 такт (на 1 момент времени) входной символ. Таким образом,при всехПостроим этот автомат. ПустьВ качестве множества состояний возьмём то же множество:Тогда полагаем:Здесь текущее состояние “запоминает” поступившую букву входного алфавита, а выходной буквой является предыдущее состояние, т.е. “запомненная” буква.

Автоматы определённые в этом параграфе, называютсяавтоматами Мили. Определим теперьавтомат Мура, или автомат без выхода.

Определение. Автоматом Мура называется тройкагдемножества, аотображение.

Множества иназываются соответственно входным алфавитом и множеством состояний. Предполагается, что множестваиконечны, хотя во многих вопросах это не имеет значения. Функцияназывается функцией переходов. Равенствоозначает, что если автомат находится в состояниии принимает символа, то должен осуществиться его переход в состояние

Покажем, что на самом деле в автомате Мили можно “избавиться” от выходного алфавита В, увеличив соответствующим образом множество состоянийт.е.автомат Мили эквивалентен в определённом смысле подходящему автомату Мура. Пусть дан автомат МилиПостроим автомат МураВ качестве множества состояний нового автомата возьмёмвходной алфавит сохраним прежним:а функциюопределим следующим образом:

Автомат Мура эквивалентен автомату Милив том смысле, что“работает” так же, какно реакцией на входной сигнал является не выходной символа изменённое более сложным образом состояние, в котором фактически “зашифрован” выходной символ