Примеры решения задач

Пример 1.Автомат задан таблицей 3.5.

О

Табл. 3.5

пределить:

Решение.

поэтому

поэтому

П

Рис. 3.12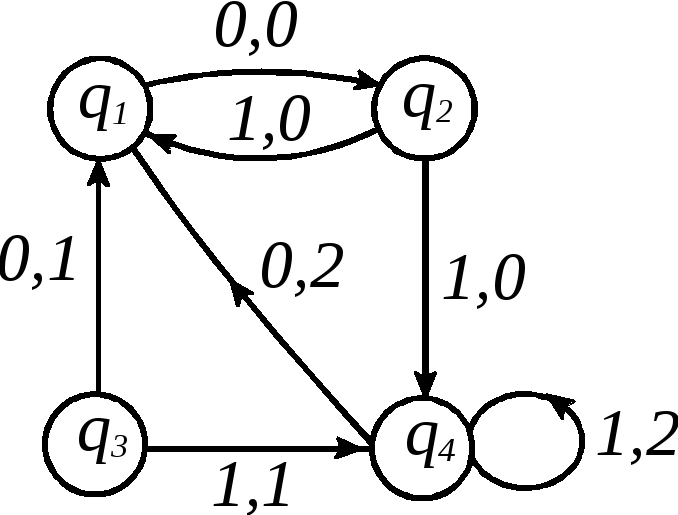

ример 2.Автомат задан диаграммой Мура, изображенной на рис. 3.12. Найти:,.

Решение.Имеем:

поэтому

Задачи для самостоятельного решения

1

Табл. 3.6

Рис. 3.13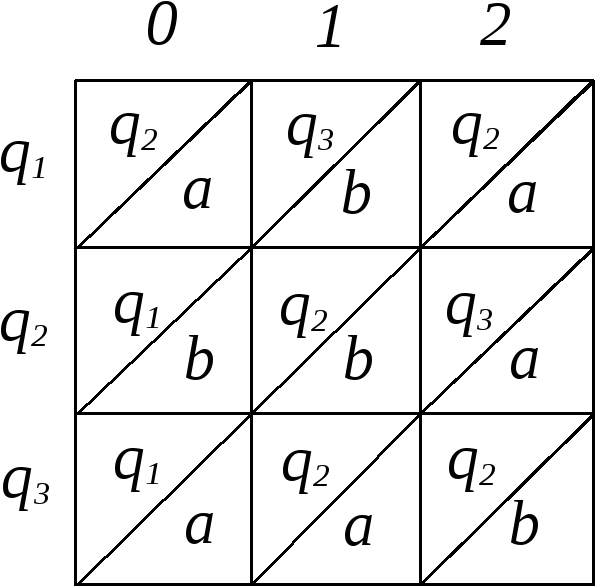

. Автомат задан таблицей 3.6. Найти: а)б)

2. Автомат задан диаграммой Мура, изображенной на рис. 3.13.

Найти: а) б)в)

г)

3. Автомат задан каноническими уравнениями

где и вычисления производятся по модулю 3. Найти: а), б).

Ответы:

1. а)б)2. а)б)в)г)3. а)2;

б)0020.

§3.4. Приведённый автомат

Назовём состояния иавтоматанеотличимыми, еслидля всехСостоянияиотличимы, еслипри некоторомПоложимеслиинеотличичимы. Нетрудно видеть, что отношение неотличимости ~ на множествесостояний автоматаявляется отношением эквивалентности. Это отношение вызывает разбиение множествана непересекающиеся классы эквивалентности:При этом любые два состояниялежащие в одном классе, неотличимы, а любые два состояния из разных классов отличимы.

Множество классов отношения ~ (фактор-множество обозначим черезПостроим новый автоматВ качестве входного и выходного алфавитов автоматавозьмём те же множестваикоторые были у автоматаа в качестве множества состояний возьмём множествоНадо определить теперь функциии

Пусть Наиболее естественным является следующее определение значениявзять какой-нибудь элементпринадлежащий классунайтиа затем класс, в котором лежит элементобъявить значениемТо есть считать, что

(1)

Докажем корректностьэтого определения, т.е. независимость от выбора представителя в классе эквивалентности. ПустьОпределение будет некорректным, если окажется, чтоДокажем, что определение корректно. Еслитопри некоторомЭто означает, чтоСледовательно,что противоречит условию. Итак,поэтому определение (1) корректно.

Функцию определим напо формуле

(2)

По определению неотличимости состояний мы имеем поэтому определение (2) корректно.

Автомат называетсяприведённым автоматом, соответствующим автомату

Докажем, что у приведённого автомата все состояния отличимы друг от друга. ПустьТогдадля всехОтсюда по формуле (2) получаем, чтопри всехСледовательно,Отсюда следует, чтоИтак, у автоматанеотличимыми являются только совпадающие друг с другом состояния.

Автомат и приведённый автоматработают одинаково: для любой входной последовательностипоследовательностьна выходе автоматаи автоматаодна и та же:и т.д. (здесьначальное состояние).

Решение типовых задач

Пример 1.Построить приведённый автомат для автомата, заданного следующей диаграммой Мура, изображенной на рис. 3.14.

Решение.Вычислим:,,,,. Следовательно, состояниеотличимо от всех остальных. Мы получаем (пока) следующее разбиение множествана классы, т.е. непересекающиеся подмножества:(далее это разбиение будет измельчаться).

Д

Рис. 3.14.

алее вычисляем:Отсюда следует, чтоне может лежать в одном классе силисилии т.д. Разбиение, полученное ранее, измельчается до следующего:ПоложимПокажем, что это окончательное разбиение. Имеем:поэтомуАналогично получаеми т.д., т.е. функция“не разбивает” классы. Следовательно, классыможно считать состояниями нового автомата. Это и есть приведённый автомат, его диаграмма Мура изображена на рисунке 3.15.

Рис. 3.15.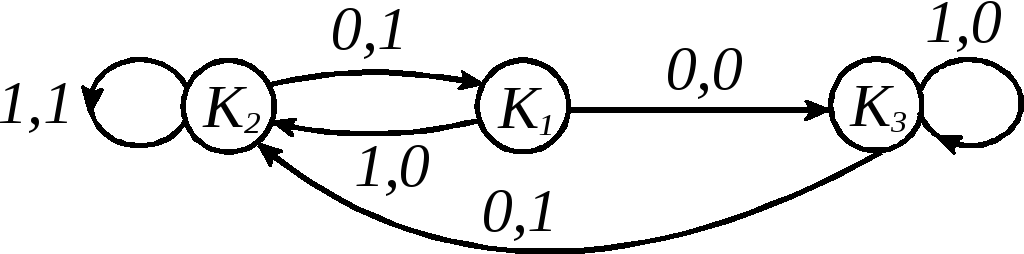

П

Табл. 3.7

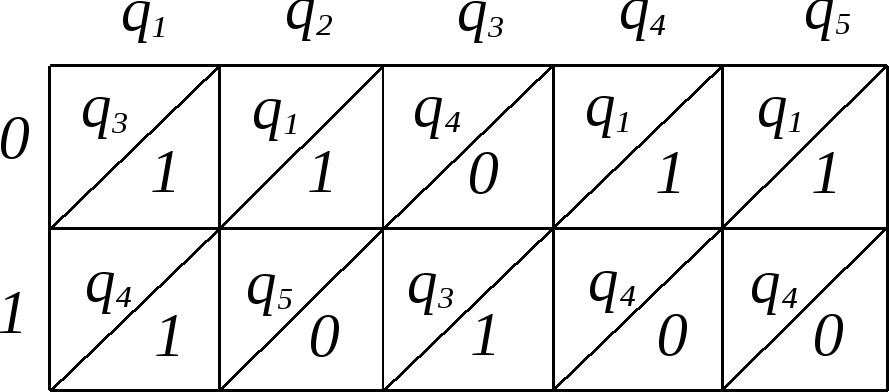
ример 2.Построить приведённый автомат для автомата, заданного следующей таблицей 3.7:

Р

Табл. 3.8

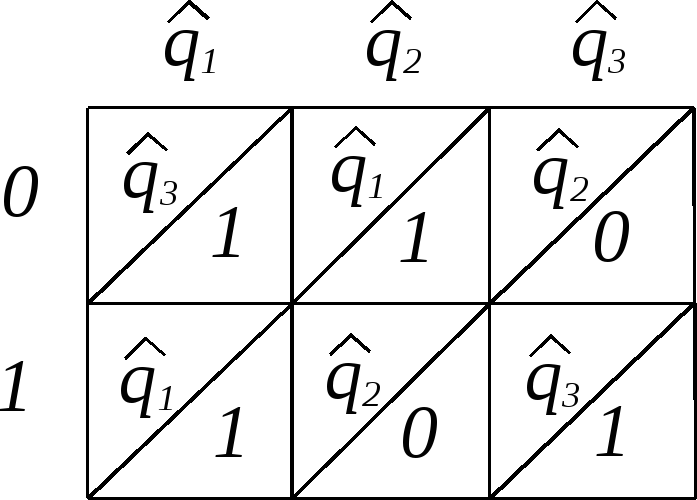
ешение.Верхняя строка таблицы 11011 определяет разбиениенижняя строкаразбиениеИх пересечениеэто разбиениеДокажем, что состояниянеотличимы друг от друга. В столбцах таблицы, соответствующих этим состояниям, мы имеем:значит, функцияна состоянияхпринимает одинаковые значения. Кроме того, другая часть столбцов:такова, чтолежат в одном классе разбиения. Это доказывает, чтонеотличимы. Из таблицы автомататеперь нетрудно получить таблицу приведённого автоматадля этого достаточно взять по одному представителю в каждом классе разбиенияТаким образом, мы получаем таблицу 3.8: