Литература / Прокофьевская книга по дискретке / glava3-5

§3.5. Периодичность выходной последовательности

конечного автомата

Мы докажем, что любой конечный автомат перерабатывает периодическую входную последовательность в периодическую выходную, период которой не превышает где период входной последовательности, а количество состояний автомата. Доказательство будет основываться на следующем (легко доказываемом) замечании: если входная последовательность имеет период а последовательность состояний автомата – период то выходная последовательность будет иметь период НОК где НОК обозначает наименьшее общее кратное.

В теореме этого раздела и во многих других вопросах теории автоматов будет удобно использовать сокращённые обозначения для функций и А именно, пусть автомат, и Если то этот факт мы будем записывать просто: Аналогично этому вместо записи будем использовать сокращённую запись

Теорема. Если входная последовательность конечного автомата является периодической, то выходная последовательность также периодическая.

Доказательство. Пусть конечный автомат. Предположим, что на вход автомата поступает периодическая последовательность Если её период, то при где момент времени, с которого начинается период. Введём в рассмотрение следующие слова:

предпериод входной последовательности и

период. Пусть начальное состояние автомата. Положим Рассмотрим последовательность состояний Так как число членов этой последовательности равно то среди них есть совпадающие, т.е. существуют различные такие, что Можно считать, что Тогда где и Итак, Докажем теперь периодичность последовательности Пусть Тогда где Получаем:

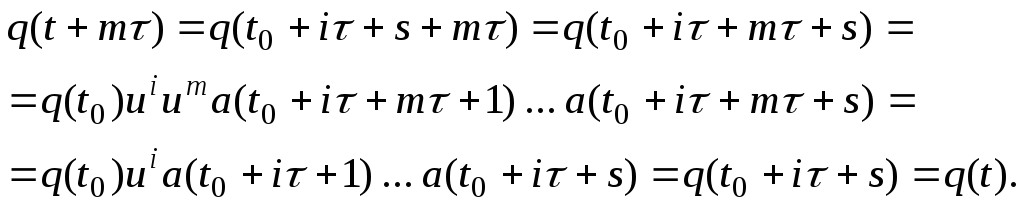
По условию последовательность периодическая с периодом по только что доказанному периодическая с периодом Отсюда, используя канонические уравнения автомата, выведем периодичность выходной последовательности. Действительно, если то

Теорема доказана.

§3.6. Теоремы Мура

Отличимость состояний конечного автомата устанавливают обычно с помощью тестирования. А именно, если автомат, находясь в состоянии и находясь в состоянии будет по-разному реагировать на одну и ту же входную последовательность, то состояния и отличимы. Если на данную тестовую последовательность ответ будет одинаковым (т.е. то можно либо удлинить входную последовательность, добавив элементы либо сменить входную последовательность, заменив её на и т.д. Таким способом можно будет установить отличимость состояний и (если они действительно отличимы), но неотличимость этот способ доказать не позволит, так как невозможно перебрать бесконечное множество последовательностей. Естественно возникает вопрос: сколько тестовых последовательностей и каких достаточно для установления неотличимости двух состояний? Ответ даёт первая теорема Мура: если количество состояний автомата, то для установления отличимости или неотличимости его состояний достаточно подавать на вход последовательности длины Для двух автоматов и имеющих одинаковые входные и одинаковые выходные алфавиты, справедлива вторая теорема Мура: для отличимости или неотличимости состояний и этих автоматов достаточно ограничиться входными последовательностями длины где и количества состояний автоматов и

Для дальнейшего нам понадобится ввести некоторые определения и обозначения. Если входной алфавит, то, как обычно, множество всех слов (произвольной длины) с буквами из Для обозначает длину словат.е. количество входящих в него букв. Определим произведение двух подмножеств множества положив

В частности, множество всех слов длины Очевидно, при (при этом считаем, что где пустое слово).

Пусть подмножество множества Будем говорить, что состояния автомата отличимы множеством если существует непустое слово такое, что Если же, наоборот, для всех непустых то и неотличимы множеством Заметим, что из неотличимости состояний и следует их неотличимость множеством для любого Обратно, если отличимы каким-либо множеством то и отличимы.

Для автоматов и с одинаковыми входными и выходными алфавитами аналогичным образом вводятся понятия отличимости (неотличимости) состояний и а также отличимость (неотличимость) множеством

Пусть конечный автомат. Для подмножества обозначим через отношение неотличимости с помощью т.е. в случае, когда и неотличимы с помощью Ясно, что отношение эквивалентности. Обычная неотличимость – это неотличимость с помощью т.е. Очевидно, т.е. разбиение множества определяемое отношением это измельчение разбиения, определяемого (каждый -класс является объединением одного или нескольких -классов). Итак, наиболее мелким (дробным) из рассматриваемых разбиений является Доказательства теорем Мура будут основываться на двух леммах.

Лемма 1. Пусть и Если то неотличимость состояний равносильна их неотличимости с помощью множества (Другими словами, при выполнении условий леммы мы имеем равенство

Доказательство. Положим Так как то Предположим, что утверждение леммы неверно, а значит, существуют состояния неотличимые с помощью но отличимые каким-нибудь словом Будем считать, что выбраны так, что слово является наиболее коротким из всех возможных. Имеем: Заметим, что слово не может состоять из одной буквы. Действительно, если то а значит, и отличимы множеством Так как то и отличимы множеством . Но по условию , поэтому и отличимы с помощью множества Однако, это противоречит выбору и

Итак, Следовательно, где а непустое слово. Положим Так как неотличимы множеством то следовательно, Таким образом, состояния отличимы словом причём Так как самое короткое слово, то и отличимы с помощью Отсюда следует, что и отличимы множеством а значит, и множеством Мы получили противоречие с выбором состояний и Лемма доказана.

Лемма 2. Пусть и Тогда существует такое что

Доказательство. Рассмотрим следующую последовательность подмножеств множества Очевидно, при всех Так как то

Докажем, что в этой цепочке включений обязательно есть точное равенство. Действительно, пусть Обозначим через количество классов, на которые множество разбивается отношением Очевидно, Так как то а значит, Рассуждая аналогично, получим: Однако, это невозможно, так как Мы получили противоречие. Следовательно, при некотором Это означает, что По лемме 1 мы получаем теперь, что

Замечание. Ранее было отмечено, что осуществляет наиболее мелкое разбиение множества Следовательно, если в цепочке в каком-нибудь месте будет иметь место равенство: то все остальные включения также будут равенствами:

Первая теорема Мура. Если состояния автомата отличимы, то они отличимы словом длины где То есть существует такое что

Доказательство. Положим и т.д. По лемме 2 существует такое, что Но Следовательно, Отсюда вытекает, что Таким образом, любые два отличимых состояния являются отличимыми с помощью множества слов длины Теорема доказана.

Вторая теорема Мура. Пусть и два автомата с одними и теми же входным и выходным алфавитами. Состояния и являются отличимыми в том и только том случае, если они отличимы множеством где

Доказательство второй теоремы Мура проведём, сведя её к первой

теореме. Очевидно, мы можем считать, что Построим новый автомат полагая

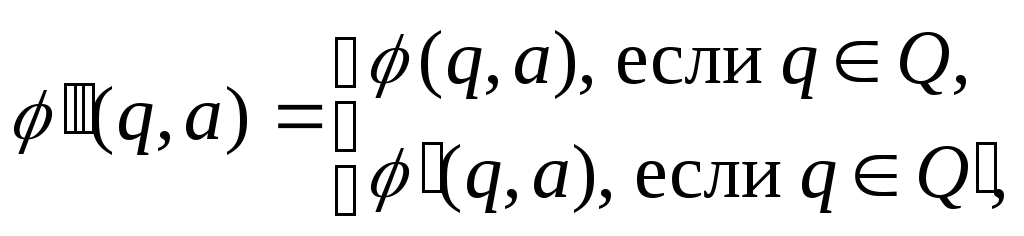
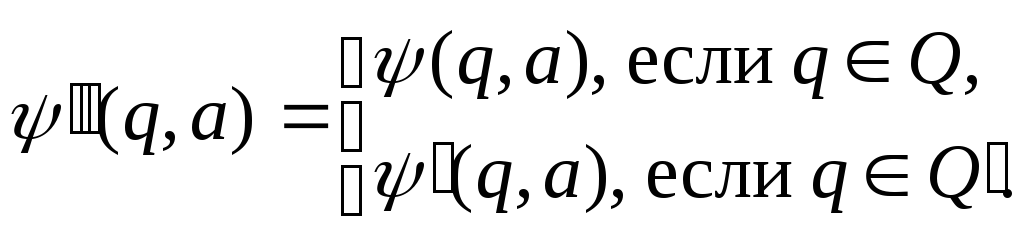
Возьмем любые состояния и Если эти состояния отличимы как состояния автоматов и то они отличимы и как состояния автомата Применив к автомату первую теорему Мура, получим, что и отличимы множеством (поскольку Таким образом, при некотором Но это означает, что Теорема доказана.

Приведём теперь пример, показывающий, что для установления отличимости состояний автомата с может оказаться недостаточно брать последовательности длины т.е. число в формулировке первой теоремы Мура не может быть уменьшено.

П

Табл. 3.13

ример. Рассмотрим автомат, представленный таблицей 3.13:

Состояния и отличимы словом Действительно, а В то же время слова длины эти состояния не отличают, так как если то

163