
- •Глава 3. Автоматы §3.1. Определение и примеры автоматов
- •§3.2. Диаграмма Мура и таблица автомата
- •Примеры решения задач
- •(А) (б) (в)
- •Задачи для самостоятельного решения
- •3. §3.3. Продолжение функций и
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Ответы:
- •§3.4. Приведённый автомат
- •Решение типовых задач
- •Задачи для самостоятельного решения
- •1 А) б) Рис. 3.18.
- •2 Табл. 3.11 Табл. 3.12 а) б).
§3.2. Диаграмма Мура и таблица автомата
Наряду с каноническими уравнениями работа автомата может быть описана с помощью диаграммы Мура или таблицы.
Определение.Диаграммой Мураавтомата![]() называется ориентированный граф,
вершинами которого являются состояния
называется ориентированный граф,
вершинами которого являются состояния![]() и для каждого равенства вида
и для каждого равенства вида![]() граф имеет ребро, идущее из
граф имеет ребро, идущее из![]() в
в![]() на котором стоит метка
на котором стоит метка![]() где
где![]()
Н
Рис. 3.4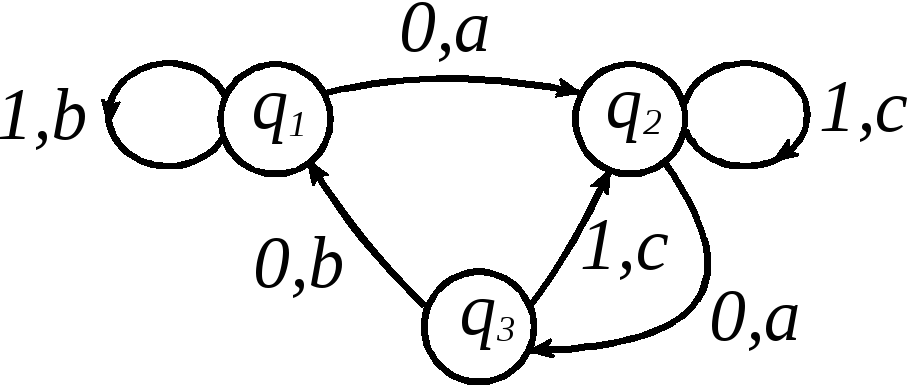
![]()
![]()
![]()
![]()
![]()
![]()
![]()
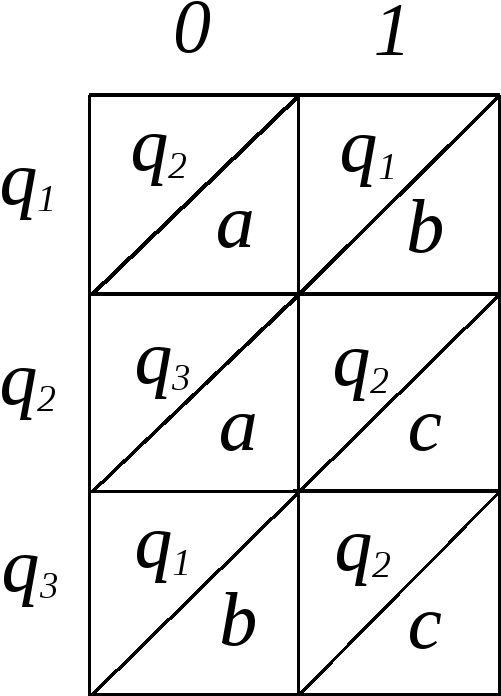
Таблицей
автомата ![]() называется прямоугольная таблица с
называется прямоугольная таблица с![]() строками и
строками и![]() столбцами, причём в клетке, стоящей на
пересечении
столбцами, причём в клетке, стоящей на
пересечении![]() -й
строчки и
-й
строчки и![]() -го
столбца написаны символы
-го
столбца написаны символы![]() и
и![]()
Н
Табл. 3.1
Примеры решения задач
З
Рис. 3.5
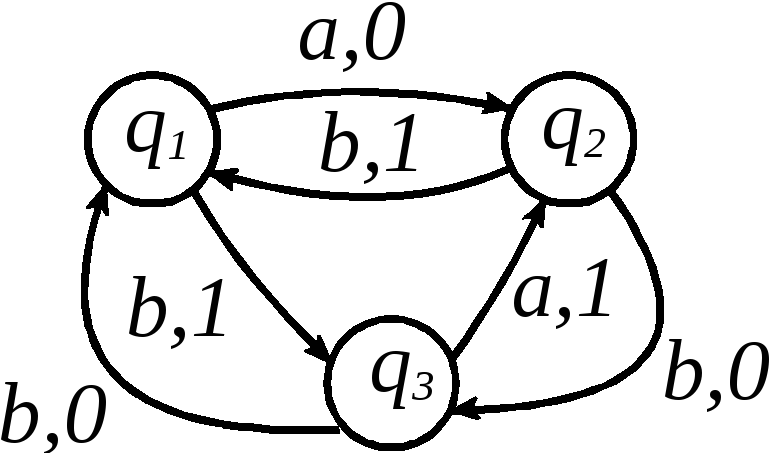

(А) (б) (в)
Решение.
Граф (а) не является диаграммой Мура
никакого автомата, так как на диаграмме
не указано, в какое состояние должен
переходить автомат, если он находится
в состоянии![]() и получает на входе символ 1.
и получает на входе символ 1.
Граф
(б) также не является диаграммой Мура,
так как переход из состояния
![]() при получении символа
при получении символа![]() определён неоднозначно.
определён неоднозначно.
Граф (в) является диаграммой Мура конечного автомата.
Из
определения конечного автомата и
диаграммы Мура следует, что ориентированный
граф, ребра которого помечены символами
![]() (
(![]() является диаграммой Мура некоторого
конечного автомата в том и только том
случае, если из каждого состояния
является диаграммой Мура некоторого
конечного автомата в том и только том
случае, если из каждого состояния![]() выходит по одной стрелке для каждого
символа
выходит по одной стрелке для каждого
символа![]()
З
Рис. 3.6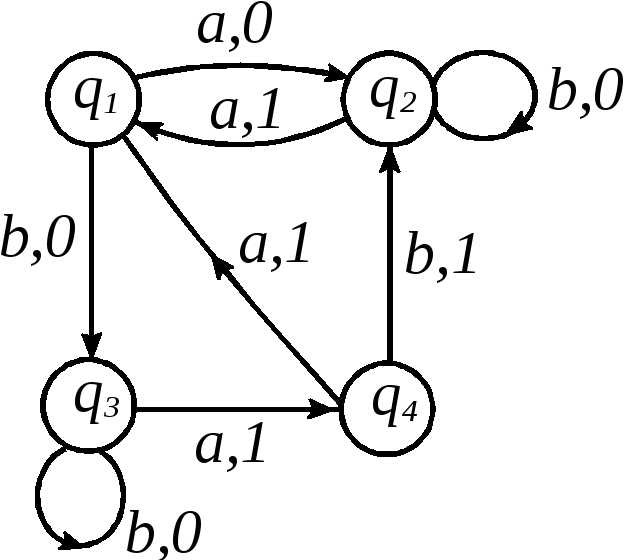
Р
Табл. 3.2
![]() и
и![]() то в клетке
то в клетке![]() надо записать символы
надо записать символы![]() и 0. Аналогично заполняются другие клетки
таблицы, и мы получаем табл. 3.2.
и 0. Аналогично заполняются другие клетки
таблицы, и мы получаем табл. 3.2.
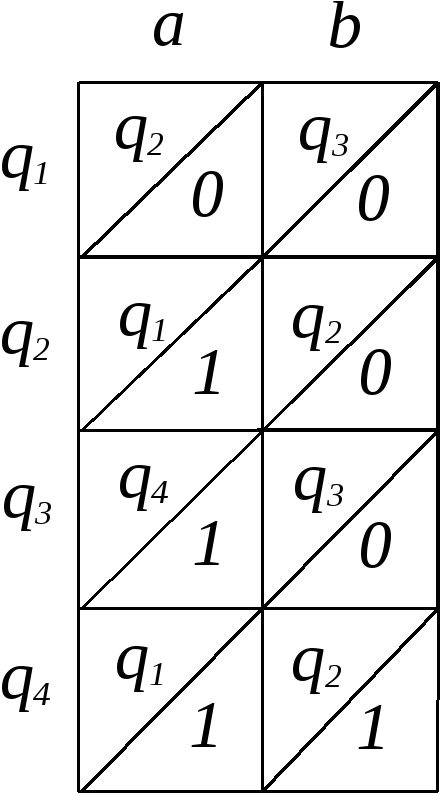
Задача 3.Построить диаграмму Мура автомата, заданного таблицей 3.3.
Р
Табл. 3.3

![]() и приняв символ 0, должен перейти в
состояние
и приняв символ 0, должен перейти в
состояние![]() и выдать на выход символ 2. Следовательно,
из
и выдать на выход символ 2. Следовательно,
из![]() в
в![]() должно идти ребро, помеченное символами
0 и 2 (см. рис. 3.7).
должно идти ребро, помеченное символами
0 и 2 (см. рис. 3.7).
Р
Рис. 3.7
Рис. 3.8![]()

Задача
4.Автомат, у которого![]()
![]() задан каноническими уравнениями
задан каноническими уравнениями
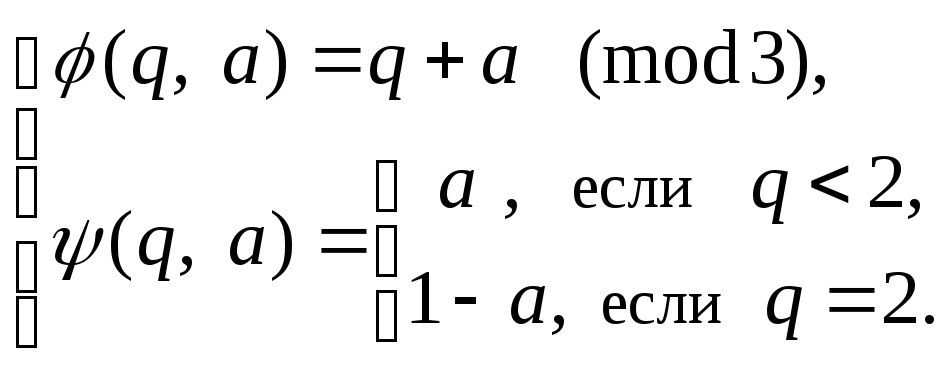
Построить диаграмму Мура этого автомата.
Р
Рис. 3.9
![]() Тогда
Тогда![]() и
и![]() Следовательно, на диаграмме Мура из
кружочка, обозначающего состояние 0, в
этот же кружочек должна идти стрелка,
помеченная символами 0, 0. Пусть теперь,
скажем,
Следовательно, на диаграмме Мура из
кружочка, обозначающего состояние 0, в
этот же кружочек должна идти стрелка,
помеченная символами 0, 0. Пусть теперь,
скажем,![]() ,
,![]() Тогда
Тогда![]() и
и![]() .
Значит, из кружочка с номером 2 в кружочек
с номером 0 идёт стрелка, помеченная
символами 0, 0. Рассматривая ана-логичным
образом остальные случаи, получим
диаграмму Мура (см. рис. 3.9).
.
Значит, из кружочка с номером 2 в кружочек
с номером 0 идёт стрелка, помеченная
символами 0, 0. Рассматривая ана-логичным
образом остальные случаи, получим
диаграмму Мура (см. рис. 3.9).
Задачи для самостоятельного решения
1.
Автомат
![]() задан каноническими уравнениями
задан каноническими уравнениями
![]()
где![]() Построить диаграмму Мура автомата
Построить диаграмму Мура автомата![]()
2.
Автомат
![]() таков, что
таков, что![]()
![]()
![]()
![]()
3
Рис. 3.10.
Ответы
1
Табл. 3.4
Рис. 3.11


3. §3.3. Продолжение функций и
Пусть
![]() конечный алфавит. Обозначим через
конечный алфавит. Обозначим через![]() множество всех слов
множество всех слов![]() Число
Число![]() называетсядлинойслова
называетсядлинойслова![]() и обозначается
и обозначается![]() Например, если
Например, если![]() то
то![]()
![]()
![]() Слово, в котором нет ни одной буквы,
будем называтьпустым словоми обозначать символом
Слово, в котором нет ни одной буквы,
будем называтьпустым словоми обозначать символом![]() Очевидно,
Очевидно,![]() Пусть
Пусть![]() множество всех слов длины
множество всех слов длины![]() а
а![]() множество всех непустых слов. Полагаем
множество всех непустых слов. Полагаем![]() .
Очевидно,
.
Очевидно,![]()
![]()
![]()
Произведениемдвух слов![]() называется слово, полученное приписыванием
к слову
называется слово, полученное приписыванием
к слову![]() справа слова
справа слова![]() Таким образом, если
Таким образом, если![]()
![]() то
то![]() Нетрудно проверить, что произведение
слов ассоциативно, т.е.
Нетрудно проверить, что произведение
слов ассоциативно, т.е.![]() для любых
для любых![]() Вообще, произведение слов
Вообще, произведение слов![]() не зависит от расстановки скобок (но
зависит от порядка сомножителей). В
частности,
не зависит от расстановки скобок (но
зависит от порядка сомножителей). В
частности,
![]()
![]()
Произведение
слов некоммутативно, так как в общем
случае
![]()
Множество,
на котором задана ассоциативная операция,
называется полугруппой.
Полугруппа![]() в которой естьединица, т.е. такой
элементе, что
в которой естьединица, т.е. такой
элементе, что![]() для всех
для всех![]() называетсямоноидом. Множества
называетсямоноидом. Множества![]() и
и![]() являются полугруппами. Кроме того,
являются полугруппами. Кроме того,![]() моноид (так как
моноид (так как![]() для всех
для всех![]() то пустое слово
то пустое слово![]() является единицей). Полугруппа
является единицей). Полугруппа![]() моноидом не является. Действительно,
если
моноидом не является. Действительно,
если![]() при некоторых
при некоторых![]() ,
то
,
то![]() ,
откуда
,
откуда![]() ,
что невозможно, так как
,
что невозможно, так как![]() .
.
Функции
![]() и
и![]() можно продолжить до функций
можно продолжить до функций![]() и
и![]() следующим образом. Положим
следующим образом. Положим
![]() при
при
![]()
![]() при
при
![]()
![]()
![]() при
при
![]()
![]() при
при
![]()
![]()
![]()
![]()
Функция
![]() несёт информацию о том, в какое состояние
перейдёт автомат, если на его вход будут
поступать последовательно несколько
букв из алфавита
несёт информацию о том, в какое состояние
перейдёт автомат, если на его вход будут
поступать последовательно несколько
букв из алфавита![]() Действительно, если в какой-либо момент
автомат находится в состоянии
Действительно, если в какой-либо момент
автомат находится в состоянии![]() а на его вход поступают буквы
а на его вход поступают буквы![]() то будут осуществляться следующие
переходы в другие состояния:
то будут осуществляться следующие
переходы в другие состояния:
![]()
![]()
т.е.
в конце концов автомат окажется в
состоянии
![]() Аналогичным образом интерпретируется
функция
Аналогичным образом интерпретируется
функция![]() А именно,
А именно,![]() где
где![]() буква, которая будет выдана автоматом
на
буква, которая будет выдана автоматом
на![]() -м
шаге.
-м
шаге.
