§1.5. Полнота, замкнутость. Теорема Поста о полноте

Для функций ифункцияназываетсясуперпозицией.

Класс булевых функций называется (функционально) полным, если любая функция изможет быть представлена в виде формулы над, т.е. любая функция получается из функций классаприменением конечного числа операции суперпозиций.

Замечание.Классможет быть конечным или бесконечным.

Примеры полных классов: а) ; б)(любая булева функция выражается формулой в виде конъюнкции, дизъюнкции и инверсии); в)любую булеву функцию можно представить в виде полинома Жегалкина.

Пусть некоторый класс булевых функций.Замыканием называется множество всех булевых функций, получающихся в виде формул над(обозначается).

Свойства замыкания:

1. .

2. .

3. .

Класс называется:

– замкнутым, если ;

– полным, если (см. определение выше);

– предполным, еслине полный, но для любой функцииклассполный.

Важнейшие замкнутые классы

Введем следующие классы функций (классы Поста):

; ;

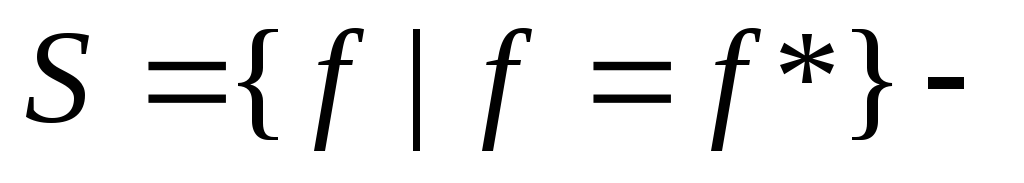класс самодвойственных функций;

класс монотонных функций (функция называетсямонотонной);

класс линейных функций (называетсялинейной).

Лемма. Классызамкнуты.

Доказательство.а) Рассмотрим функцию, где. Покажем, что. Действительно,

.

Следовательно, класс замкнут.

б) Аналогично предыдущему доказывается замкнутость класса .

в) Пусть , гдесамодвойственные функции. Тогда, т. е. .. Следовательно, классзамкнут.

г) Пусть, где. Покажем, что. ПустьНаборы переменных состоят из переменных, встречающихся у функцийсоответственно.

Возьмем два набора изначений переменных. Они определяют наборызначений переменныхпричем. Так как, то

.

Тогда . Функция, поэтому. Отсюда

.

Следовательно, класс замкнут.

д) Класс замкнут, так как линейное выражение, составленное из линейных выражений, является линейным.

Лемма (о несамодвойственной функции). Если , то из нее путем подстановки функцийивместоможно получить несамодвойственную функцию одного переменного, т.е. константу.

Доказательство.Так как, то существует набортакой, что.

Рассмотрим функцию . Пусть

.

Тогда

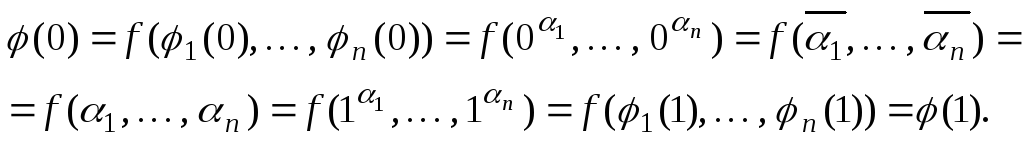
Следовательно, константа 0 или 1.

Замечание. Если, то вместоподставляем, если жето.

Замечание.Для того чтобы определить, является ли функция, заданная своим вектором значений , самодвойственной, следует проверить, получается ли вторая половина вектораиз первой отражением и последующим инвертированием его координат.

Лемма (о немонотонной функции). Если, то подстановкой констант,и функциииз нее можно получить.

Доказательство.Если, то найдутся два набора значений переменныхитакие, чтои. Поскольку наборыиразличаются вкоординатах (), то, меняя по одной координате, между ними можно вставитьсоседних наборов, т.е. таких, что

и каждый следующий набор получается из предыдущего изменением ровно одной координаты.

Так как , то в этой цепочке найдутся два соседних набора переменныхитакие, чтои. Пусть эти наборы различаются в- ой координате:

.

Рассмотрим функцию

.

Имеем

Поскольку, , то.

Замечание.Для проверки на монотонность функции, заданной своим вектором значений , нужно сначала разделить его две равные частии. Если соотношениене выполнено, тонемонотонная. В противном случае разделим каждый из полученных векторов опять пополами. Проверим сначала первую пару на выполнение соотношения, и в случае положительного результата вторую. Если хотя бы для одной пары соотношение не выполняется, то функция немонотонная. В противном случае этот алгоритм продолжаем дальше.

Лемма (о нелинейной функции). Если, то из нее путем подстановки констант,и функцийи, а также, быть может, инвертированием, можно получить функцию.

Доказательство. Возьмем полином Жегалкина для:

.

В силу нелинейности полинома в нем найдется член, содержащий не менее двух множителей. Без ограничения общности можно считать, что среди этих множителей присутствуют и. Тогда можно преобразовать полином следующим образом:

,

где в силу единственности полинома .

Пусть таковы, что. Тогда

,

где – константы, равныеили. Рассмотрим функцию, получаемую изследующим образом:

.

Очевидно, что

.

Следовательно, .

Лемма.Классы Постапопарно различны.

Доказательство.Для доказательства леммы приведем функции, лежащие в классах, но так, чтобы классы взаимно не поглощались. Рассмотрим функциии построим таблицу принадлежности классам. В таблице будем ставить «+», если функция принадлежит классу, и «–» в противном случае.

0	+	–	–	+	+
1	–	+	–	+	+
	–	–	+	–	+

Если бы какие-нибудь два класса совпадали, то совпадали бы и соответствующие столбцы таблицы. Так как они не совпадают, делаем вывод о попарном различии классов.

Теорема Поста(о полноте). Для того чтобы система функцийбыла полной необходимо и достаточно, чтобы она целиком не содержалась ни в одном из пяти замкнутых классов.

Доказательство.Необходимость.Пусть системаполна. Тогда. Допустим, чтосодержится целиком в каком-либо из классов Поста (обозначим его через), т.е.. В этом случае. Отсюда, что невозможно.

Достаточность.Пустьне содержится целиком ни в одном из пяти классов Поста. Выделим из нее подсистему функций., где, и на ее основе построим полную систему.

1. При помощи построим функции (константы) 0 и 1 или функцию.

Разберем отдельно два случая:

(а) ;

(б) .

(а) Рассмотрим функцию . Из цепочки равенствследует, что.

(б) В этом случае для функции получаем, т.е..

Аналогичным образом, используя функцию , строим константу 0 или функцию.

Итак, нами построены либо функция , либо обе константы 0 и 1. или

2. Если построена , то с помощьюи, применяя лемму о несамодвойственной функции, строим константы 0 и 1.

Если есть обе константы 0 и 1, то .с помощью функций 0, 1 и , используя лемму о немонотонной функции, можно построить.

3. При помощи 0, 1, и, применяя лемму о нелинейной функции, строим функцию.

Система полная. Значит, иполная. Отсюда следует полнота системы. Теорема доказана.

Следствие 1.Из всякой полной системы можно выделить полную подсистему, содержащую не более пяти функций.

Это утверждение можно усилить, а именно, имеет место.

Лемма.Из всякой полной системы можно выделить полную подсистему, содержащую не более четырех функций.

Доказательство.Так как, то либолибо. Тогда полная система будет состоять из функцийлибо.

Пример 1. Определить количество функций классови, зависящих от переменных.

Решение.Вектор значений функцииимеет вид, т.е. определено только значение на нулевом

наборе переменных, свободных же . Следовательно,. Аналогично вычисляется количество функций класса.

Пример 2. Определить количество самодвойственных функций, зависящих отпеременных.

Решение.Функцияпринимают противоположные значения на противоположных наборах переменных. Поэтому для ее задания достаточно задать первую половину ее вектора значений. Следовательно, количество самодвойственных функций, зависящих отпеременных, равно.

Пример 3. Определить количество линейных функций, зависящих от переменных.

Решение.Различных линейных функций от переменныхстолько же, сколько различных векторов, т.е..