Процедура упрощения д. Н. Ф. (алгоритм Блейка)

1. Удаление элементарной конъюнкции, которая представима в виде .– реализует функциюи если– тоже реализует функцию, тогда мы можем отбросить..

2. Удаление множителя. Для двух д. н. ф. итаких, что,.

Д. н. ф., которую нельзя упростить с помощью вышеприведенных методов, называется тупиковой.

Примеры:Для функциид. н. ф.– не тупиковая, а– тупиковая.

Алгоритм получения тупиковой д. Н. Ф.

1. По функции строят какую-либо д. н. ф. (с уверенностью можно говорить о построении хотя бы СДНФ). В д. н. ф. фиксируют порядок слагаемых и в каждом слагаемом порядок множителей.

2. Просматривают слева направо д. н. ф. каждую элементарную конъюнкцию на предмет упрощения:

а) возможность удаления элементарных конъюнкций;

б) возможность удаления множителя.

3. Возврат в п.2а, проводя то же (не просматривая множители).

Например, для функции .

. Получили тупиковую д. н. ф. при данном порядке следования конъюнкций и букв.

Теорема(без доказательства). Пустьи– какая-либо ее тупиковая д. н. ф. Тогда существует такое упорядочение слагаемых СДНФ, что при помощи данного алгоритма получается.

Рассмотрим также геометрическую интерпретацию построения д. н. ф. на единичном кубе.

Геометрическая интерпретация

Каждой булевой функции в булевом кубеможно поставить в соответствие множество его вершин,называемое носителем,

.

Очевидно, множество однозначно определяет функцию.

Е

Рис. 1.2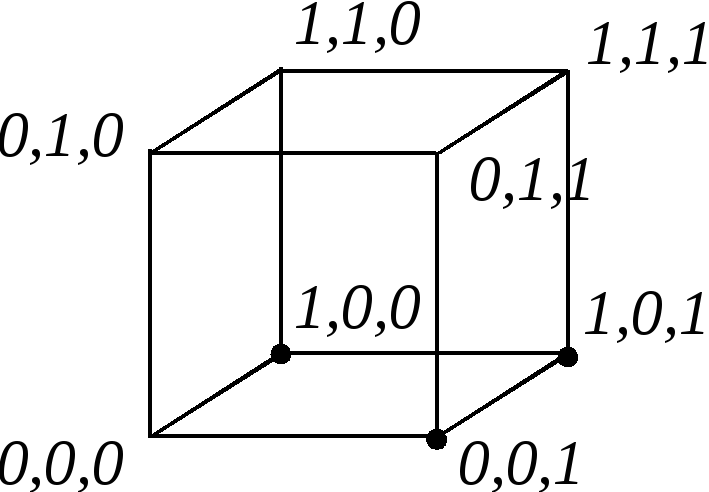

сли функция реализуется элементарной конъюнкцией, то соответствующее множествоназываетсяинтервалом -го ранга(есть-мерная грань). Очевидно, что если, то. Для функции, реализуемой д. н. ф., справедливо равенство. Еслиранг, то числоназываетсярангом покрытия.

Примеры.Носительфункциипоказан на рис. 1.2.

Для конъюнкции носитель – точка(определяют нулевую грань) (см. рис. 1.3а).

Для конъюнкции ранг равен 2, поэтому носитель – ребро(см. рис. 1.3б). Для конъюнкции

а) б) в)

Рис. 1.3

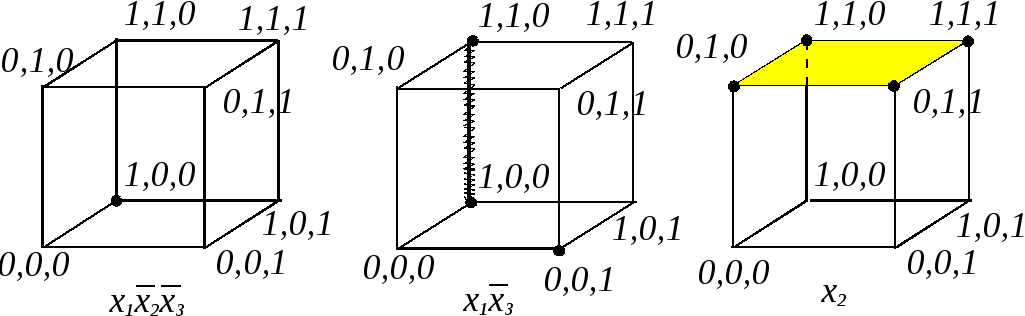
ранг равен 1; носитель – плоскость ()(см. рис. 1.3в).

Свойства носителя.

1. Если , то:

а) ,; б).

3. Для функции, представленной д. н. ф. ,.

Замечание.Проблема построения д. н. ф. сводится к покрытию носителягранями.

Пример.Носитель функциипокрывается

а

а) б) в) г)

Рис. 1.4

)(рис. 1.4а); б)(рис. 1.4б); в)(рис. 1.4в); г)(рис. 1.4г).

Сокращенная д. Н. Ф.

Конъюнкция называетсяимпликантой для функции, если.

Импликанта называется простой, если из соответствующей конъюнкциинельзя вычеркнуть ни одной переменной, чтобы оставшееся выражение было импликантой.

Пример.Для функцииконъюнкция(это импликанта, так как носителем является точка) не является простой, так как– простая импликанта. В геометрической интерпретации импликанта – наибольшая грань.

Сокращеннаяд. н. ф. – это дизъюнкция всех простых импликант (она единственна).

П

Рис. 1.5

ример.Для функцииэто два ребра.

Для функции (рис. 1.5) сокращенная д. н. ф. имеет вид.

Теорема.Минимальная д. н. ф. получается из сокращенной вычеркиванием из нее некоторых простых импликант.

Аналитические методы построения сокращенной д. Н. Ф. Метод Нельсона

1. По строят СКНФ. Например, для

СКНФ =.

2. Раскрывют скобки.

.

3. Производят упрощение по следующим правилам:

, ,

, ,.

Метод Квайна

1. По строим СДНФ. Например, для функции. СДНФ=.

2. Применяем операцию неполного склеивания

.

3. После того как такая операция применена к каждой паре конъюнкций из СДНФ, к которой она применима, с помощью операции поглощения () удаляем те конъюнкции ранга, которые можно удалить таким образом. В итоге получаем некоторую д. н. ф..

4. Если проведено этапов, то на-м этапе операции неполного склеивания и поглощения применяются к конъюнкции рангад. н. ф.. Получаем д. н. ф..

Алгоритм завершается, если .

Пример.Построить сокращенную д. н. ф. функции

.

Решение..

После первого этапа имеем .

После второго этапа имеем .

Простая импликанта называетсяядровой, если существует набортакой, что, нодля всех, входящих в сокращенную д. н. ф.

Геометрическая интерпретация: – ядровая импликанта, если существует точка, принадлежащая, которая покрывается только.

Пример.Для функциисокращенная д. н. ф. = =.

Ядровая д. н. ф.(ЯДНФ) – это дизъюнкция всех ядровых импликант.

П

Рис. 1.6

ример.На рис. 1.6 представлен носитель функции, у которой нет ядровой д. н. ф.