Задачи для самостоятельного решения
1.
Из заданного множества
 элементарных конъюнкция выделить
простые импликанты функции
элементарных конъюнкция выделить
простые импликанты функции :
:
а)
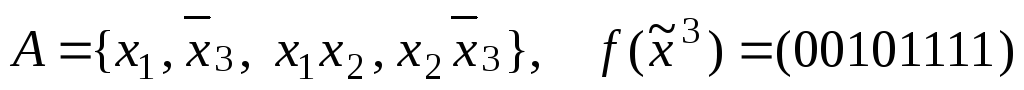 ;
;
б)
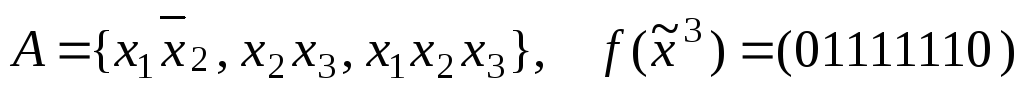 ;
;
в)
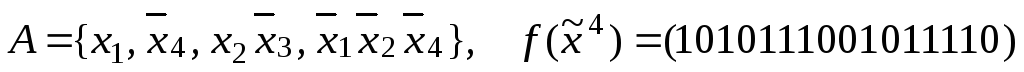 .
.
2.
Построить сокращенную д. н. ф. по заданной
к. н. ф.:
а)
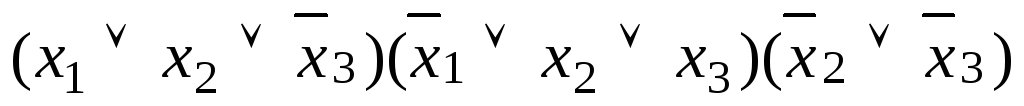 ;
;
б)
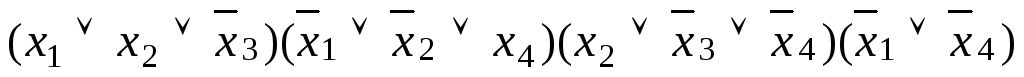 .
.
3.
Используя алгоритм Квайна, построить
сокращенную д. н. ф. функции
 :
:
а)
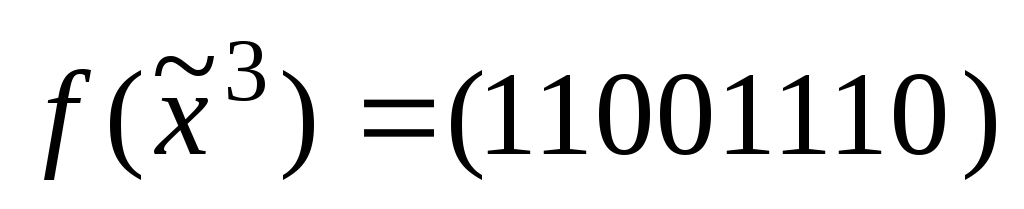 ; б)
; б)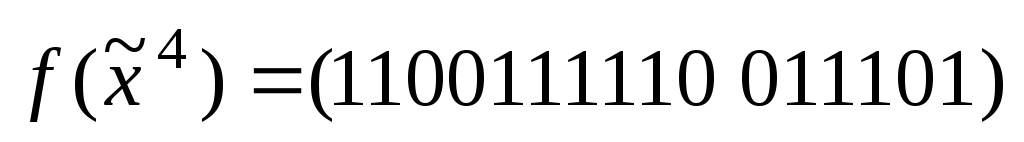 .
.
4.
Изобразив множество
 функции
функции в
в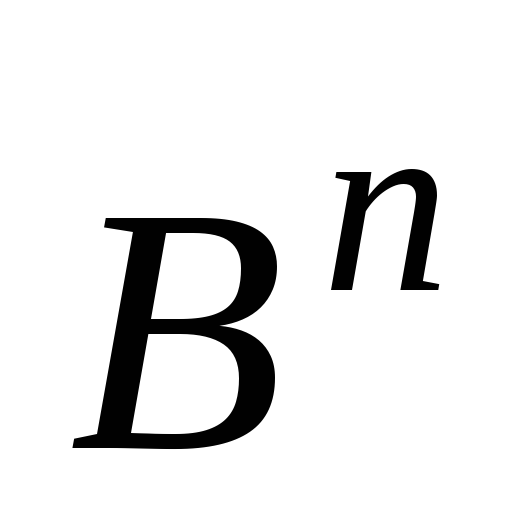 ,
найти ее простые импликаты, построить
сокращенную и ядровую д. н. ф.:
,
найти ее простые импликаты, построить
сокращенную и ядровую д. н. ф.:
а)
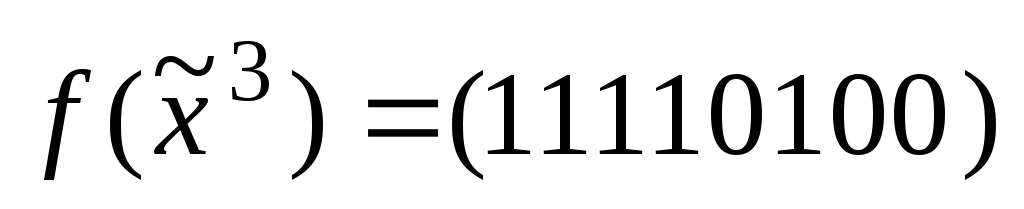 ;
;
б)
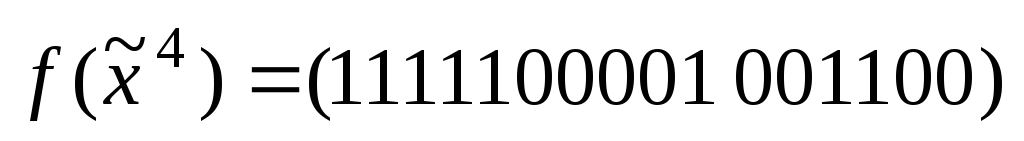 .
.
5.
Найти длину сокращенной д. н. ф. функции
 :
:
а)
 ;
;
б)
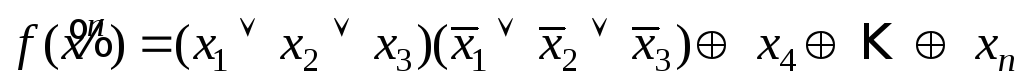 .
.
6.
Показать, что число функций, для которых
фиксированная элементарная конъюнкция
ранга
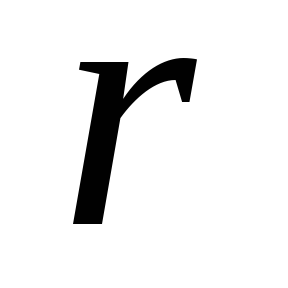 является импликантой, равно
является импликантой, равно .
.
7.
Показать, что любая функция от
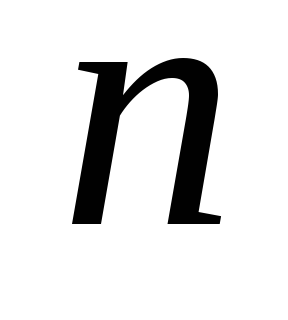 переменных может быть реализована д.
н. ф., содержащей не более
переменных может быть реализована д.
н. ф., содержащей не более элементарных конъюнкций.
элементарных конъюнкций.
8.
Показать, что число конъюнкций в тупиковых
д. н. ф. не превосходит
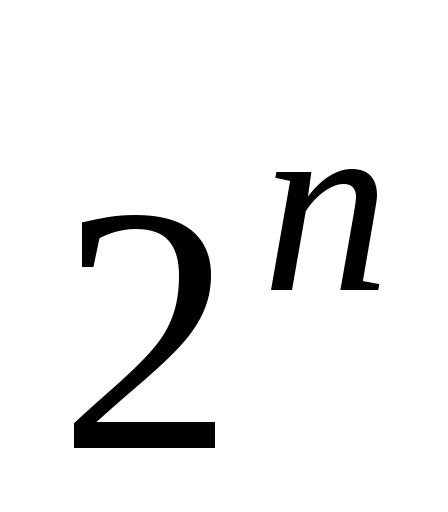 .
.
9.
Показать, что число ядровых импликант
функции
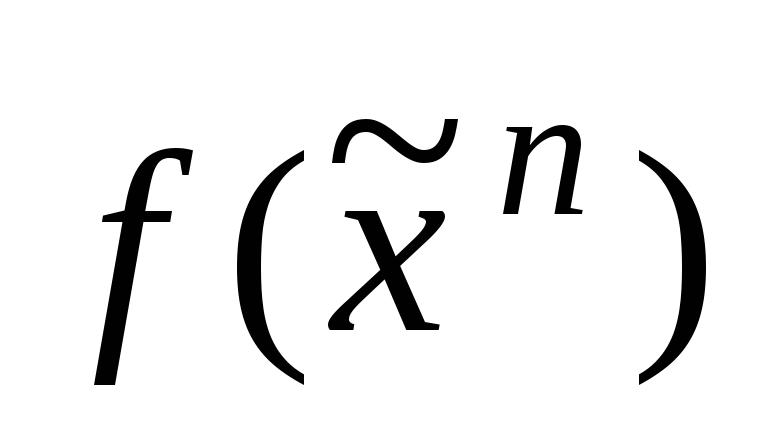 не превосходит
не превосходит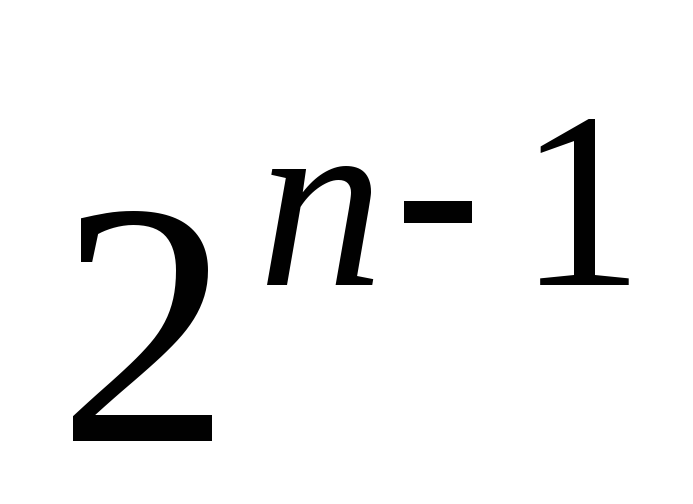 .
.
10.
Показать, что вякая простая импликанта
функции
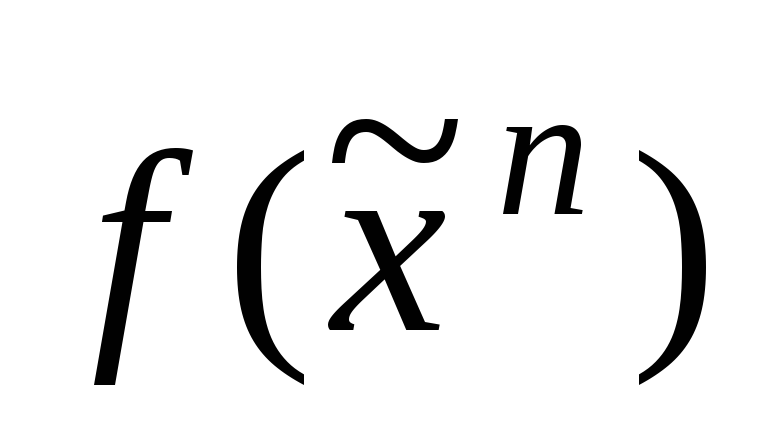 :
:
а)
ранга
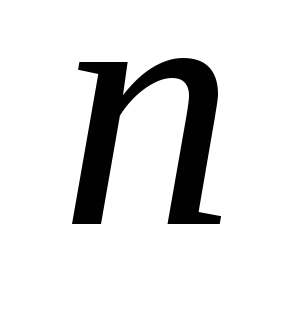 является ядровой;
является ядровой;
б)
ранга меньше 2 является ядровой.
Ответы
1.а)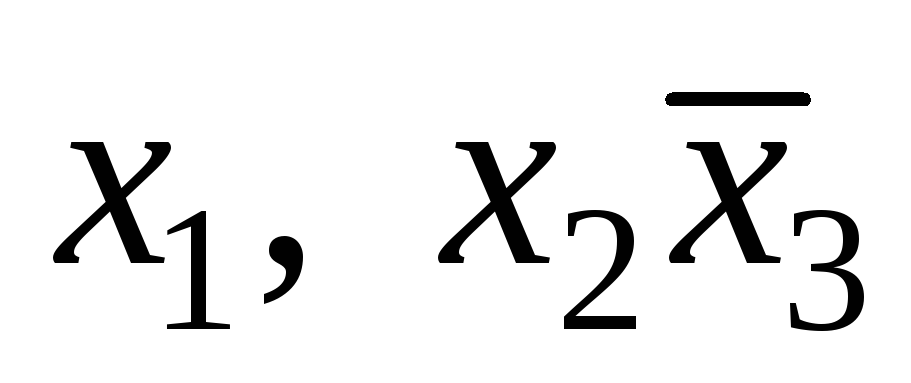 ;б)
;б)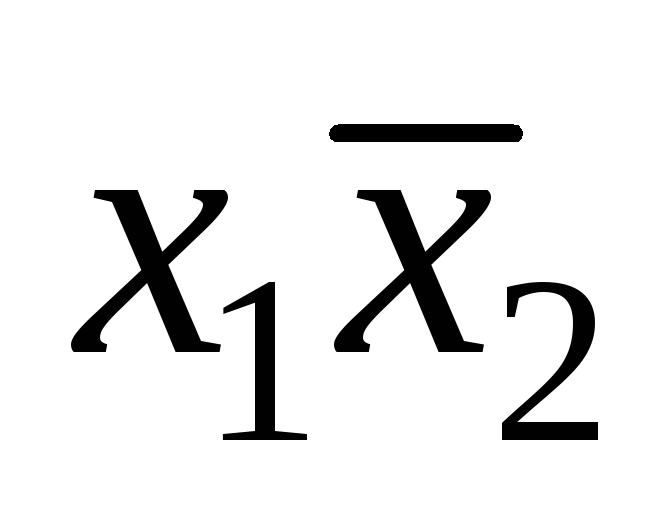 ;в)
;в)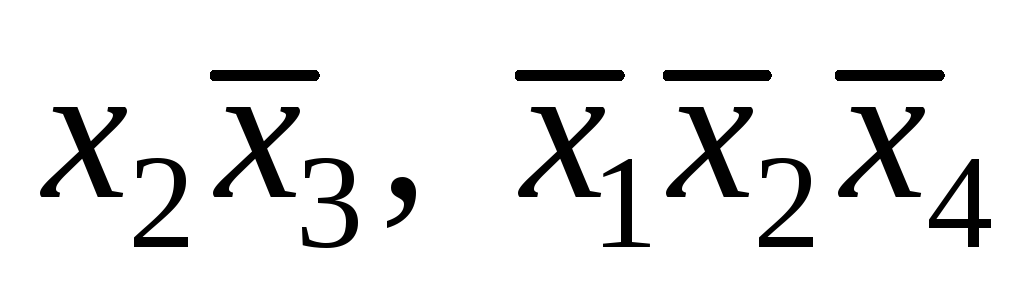 .2.а)
.2.а)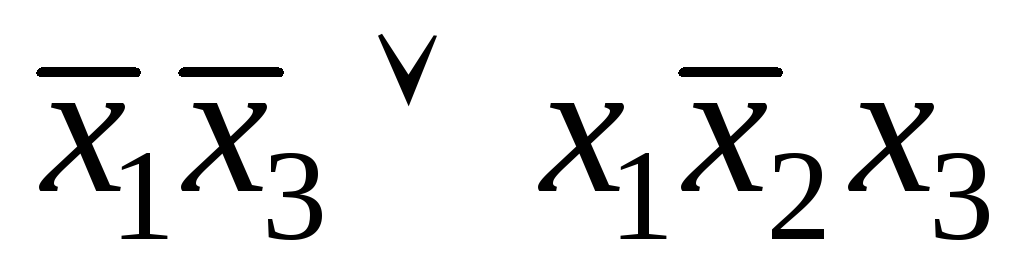 ;
;
б)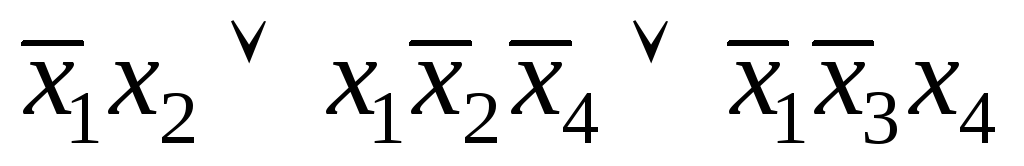 .3.а)
.3.а)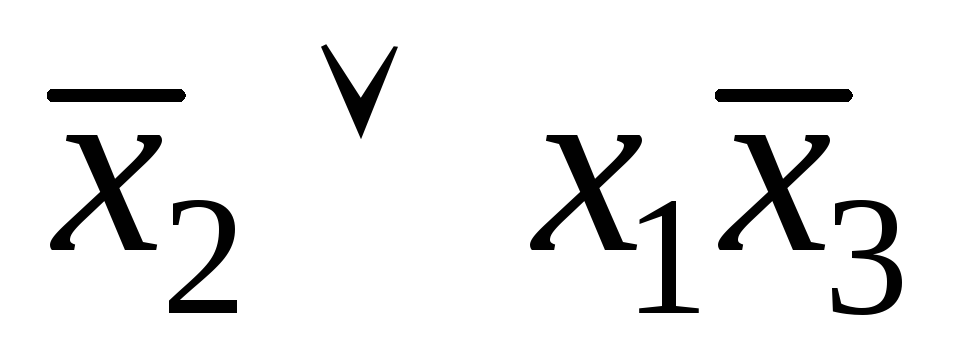 ;б)
;б)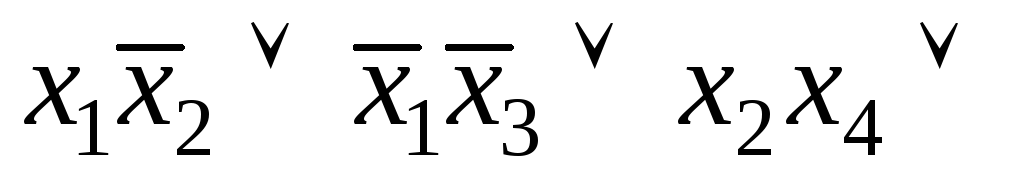
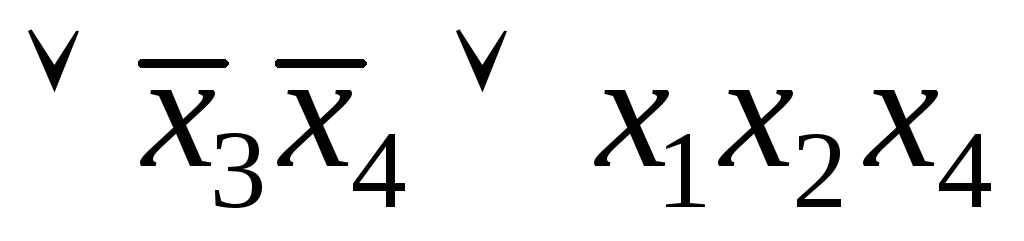 .4.а)сокращенная, она же ядровая д. н. ф.
.4.а)сокращенная, она же ядровая д. н. ф.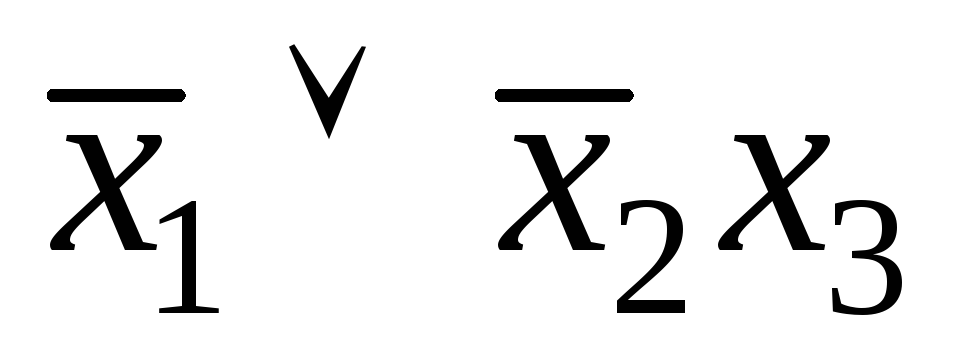 ;
;
б)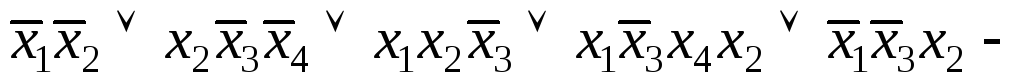 сокращенная
д. н. ф.,
сокращенная
д. н. ф.,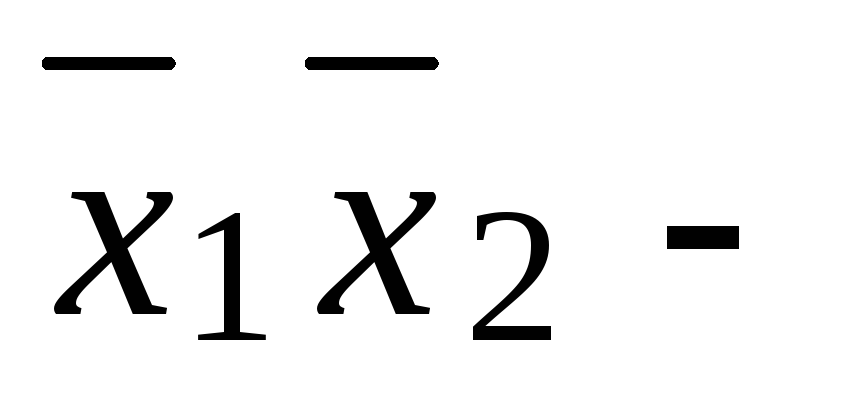 ядровая
д. н. ф.5.а)
ядровая
д. н. ф.5.а)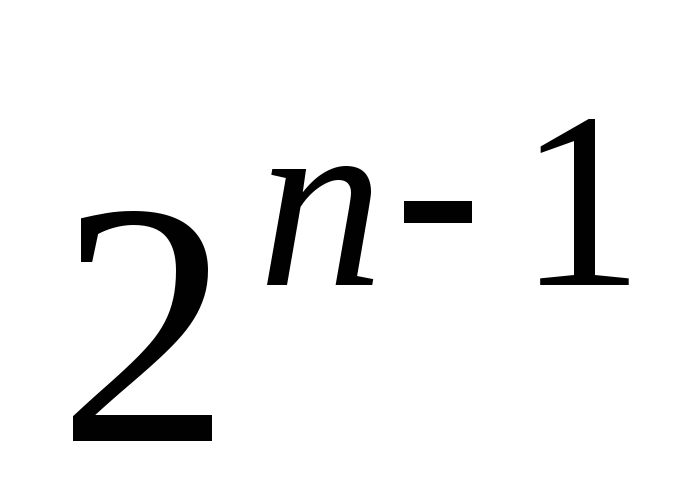 ;б)
;б)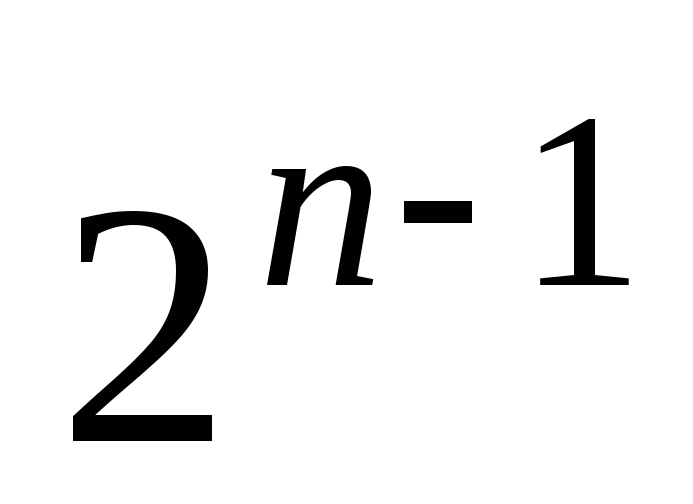 .
.
67

