Литература / Прокофьевская книга по дискретке / glava1-6

§1.7. Схемы из функциональных элементов

К

а) б)

Рис. 1.7

аждой бинарной операции в алгебре логики соответствует функциональный элемент с двумя входами и одним выходом, унарной – с одним входом и одним выходом (см. рис. 1.7). Если набор функциональных элементов (ФЭ) соответствует полной системе в , то любую булеву функцию можно выразить формулой через функции полной системы и реализовать ее с помощью соответствующих ФЭ.

Логическая схема , выходные сигналы которой описываются системой булевых функций

,

где входные сигналы логической схемы (, ), называется схемой из функциональных элементов (СФЭ).

Теорема. Для того, чтобы для произвольной системы

существовала схема из ФЭ с входами и выходами необходимо и достаточно, чтобы набор ФЭ соответствовал полной системе функций.

Обычно для построения схем используются базис 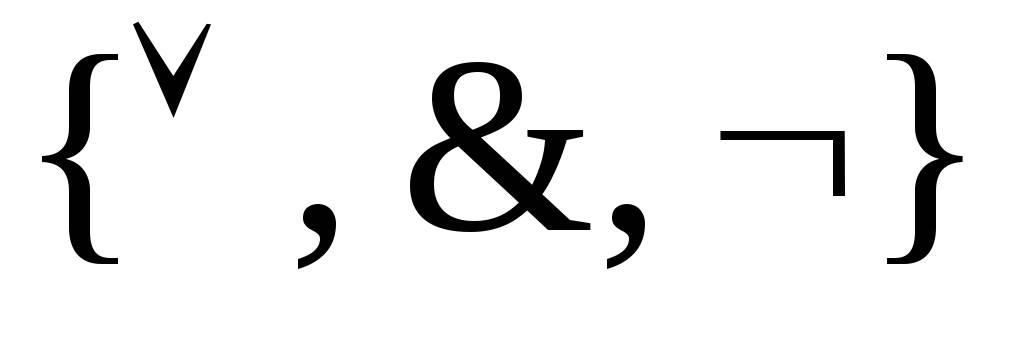(этот базис называется стандартным или булевым) или (базис Жегалкина).

Обозначим через функционал, равный числу элементов в схеме , означающий сложность схемы.

Проблема синтеза – построить схему с минимальной сложностью.

Решение типовых примеров

1

Рис. 1.8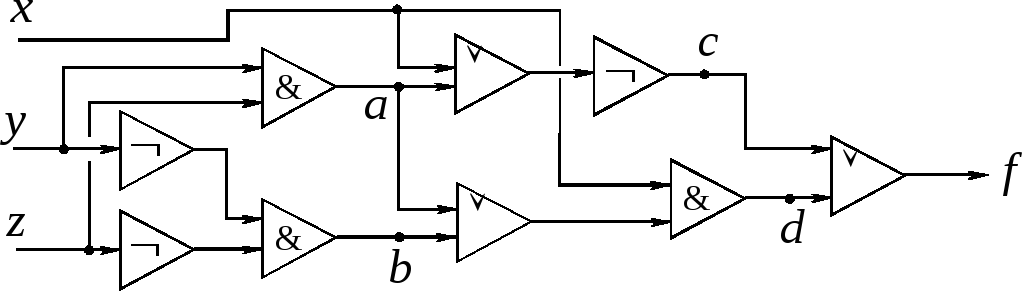

. Представить формулой функцию, заданную схемой

Решение. Имеем: Отсюда

2. Построить схему, реализующую функцию

Решение. Положим Схема, реализующая функцию, выглядит так:

Рис. 1.9

3

Рис. 1.9

Рис. 1.10

. Упростить схему (рис. 1.10).

Решение. Требуется построить схему с меньшим числом функциональных элементов, реализующую ту же функцию Для этого выразим формулой и упростим формулу. Имеем:

Рис. 1.11

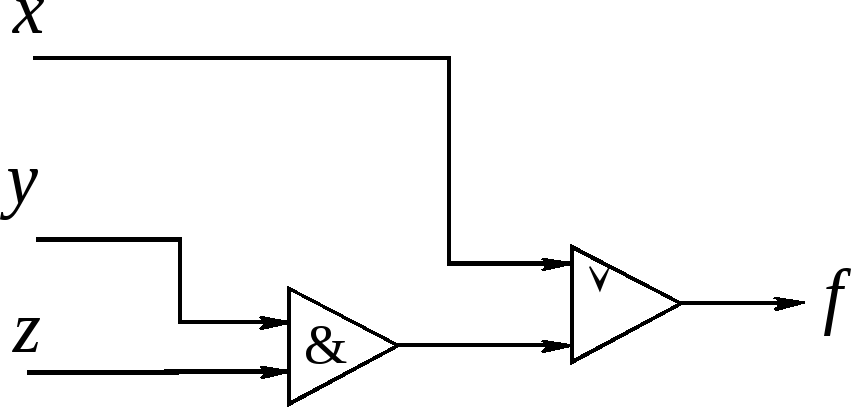
Следовательно, функция может быть реализована схемой из 2 функциональных элементов (рис. 1.11).

Задачи для самостоятельного решения

1

Рис. 1.12

. Представить формулой функцию, заданную схемой (рис. 1.12).

2. Представить схемой функцию

3

Рис. 1.13

. Упростить схему (рис. 1.13).

Ответы

1

Рис. 1.14

. (выражение не упрощено). 2. Схема изображена на рис. 1.14.

3. Схема изображена на рис. 1.15.

Рис. 1.15

§1.8. Функции -значной логики

Рассмотрим множество .

Функция называется функцией -значной логики от переменных.

Для задания функции достаточно указать ее значения на каждом наборе переменных из .

Табл. 1.12

0	0		0	0
0	0		0	1
0	0		0
0	0		1	0
0	0

Имея в виду стандартное расположение наборов (в соответствии с увеличением их номера), наборы представляют собой разложения в -ичной системе счисления чисел .

Обозначим через множество всех функций -значной логики от переменных, а множество всех функций -значной логики.

Аналогично тому, как поступали при подсчете числа булевых функций, зависящих от переменных, можно доказать следующую теорему.

Теорема. .

Замечание. Видно, что, в отличие от булевой алгебры, в при существенно возрастают сложности в эффективном использовании табличного задания функций. Так, уже в простейшем случае .

В часто используют вместо табличного задания функций задание при помощи алгоритма вычислимости функций. Например,

.

Вводя (по аналогии с ) понятие существенной и фиктивной переменной, а также понятие равенства функций, можно рассматривать все функции с точностью до фиктивной переменной.

Рассмотрим примеры некоторых считаемых элементарными функций .

1) – константы.

2) , где представляет собой обобщение отрицания в смысле “циклического” сдвига значений – отрицание Поста.

3) , где (часто обозначают ) представляет собой обобщение отрицания в смысле “зеркального” отображения значений, – отрицание Лукашевича.

4) – характеристическая функция (первого рода) числа .

5) – характеристическая функция (второго рода) числа .

6) – обобщение конъюнкции (другие обозначения: , ) – минимум и .

7) – другое обобщение конъюнкции – произведение и по модулю .

8) – обобщение дизъюнкции (другое обозначение: ) – максимум и .

9) – сумма и по модулю .

10) 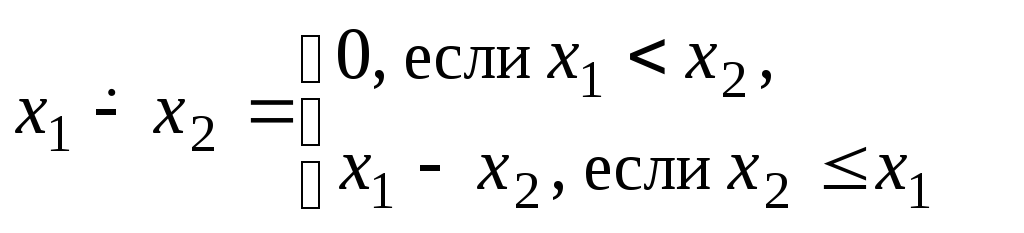– усеченная разность.

11)

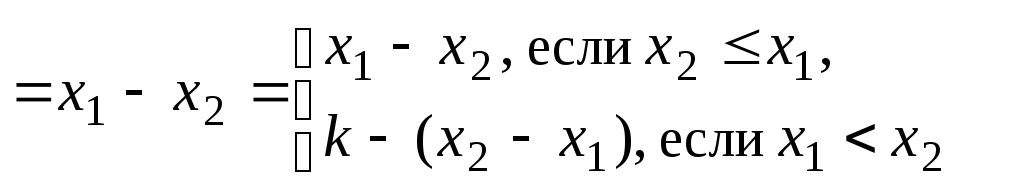– разность и по модулю (функция Вебба).

12) – импликация.

Следующие равенства вводятся по определению.

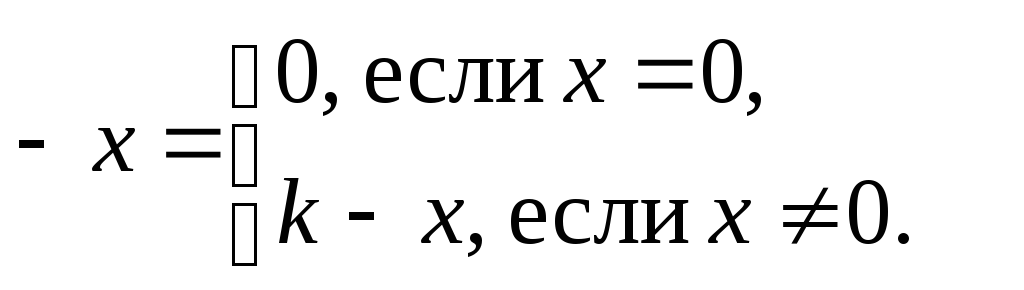
По аналогии с булевой алгеброй в -значной логике:

• вводится понятие формулы над множеством функций ;

• каждой формуле ставится в соответствие функция и говорится, что формула реализует функцию ;

• формулы и считаются эквивалентными, если соответствующие им функции и 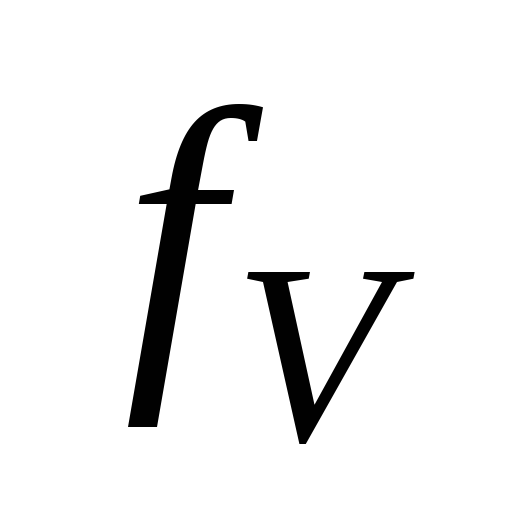равны.

Обратим внимание на то, что

1. в -значной логике сохраняются многие свойства и результаты, которые имеют место в двузначной логике;

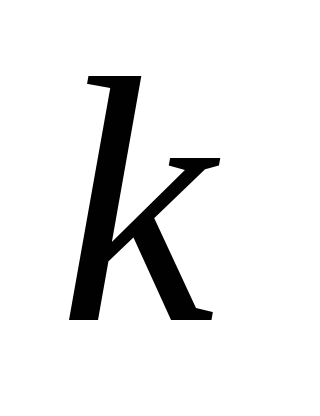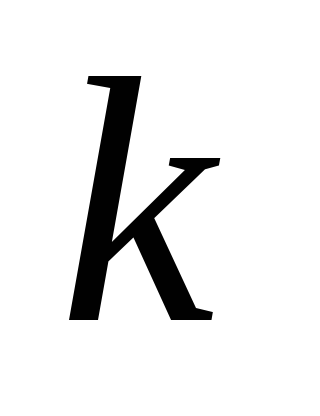2. в -значной логике при имеются принципиальные отличия от алгебры логики.

Так, имеют место равенства:

1. Коммутативность

, где .

2. Ассоциативность

, где .

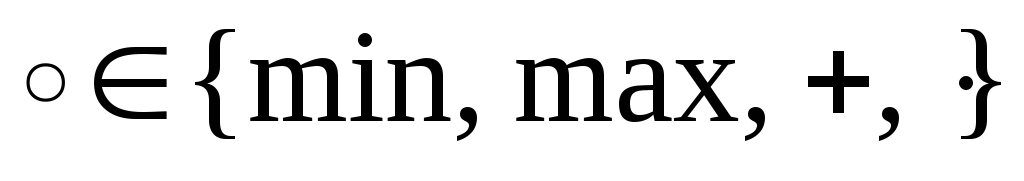3. Дистрибутивность умножения относительно сложения

.

4. Дистрибутивность операции относительно операции

.

5. Дистрибутивность операции относительно операции

.

6. Идемпотентность операций и

.

7. Аналоги правил де Моргана в

.

Следующее важное тождество, доказываемое непосредственной проверкой, представляет собой аналог СДНФ

.

Приведем примеры отличия -значной логики (при ) от двузначной:

1. При , но при всех ;

2. , но

Класс функций из называется (функционально) полным, если любая функция из может быть представлена в виде формулы над .

Пример. Система полная.

Теорема. Система функций

является полной в .

Доказательство. Пусть – произвольная функция .

Для нее имеет место разложение

.

Данная формула (правая часть) построена из функций, входящих в систему . Такое представление функции называется первой формой.

Для функций из справедливо еще одно представление, называемое второй формой

.

Если простое число, то, как и в случае двузначной логики, каждая функция представима, и притом единственным образом, в виде полинома Жегалкина

где а операции сложения и умножения производятся по модулю символ понимается в обычном смысле:

Наконец, если где простое число, то можно установить взаимно однозначное соответствие между множеством и полем (из элементов). Отождествим соответствующие элементы множеств и т.е. будем считать, что на множестве заданы операции сложения и умножения, превращающие это множество в поле из элементов (эти операции не следует путать со сложением и умножением по модулю , ведь кольцо не является полем). Теперь мы можем представлять функции в виде полиномов Жегалкина

где а операции такие, как в поле .

Пример. Представим функцию 3-значной логики

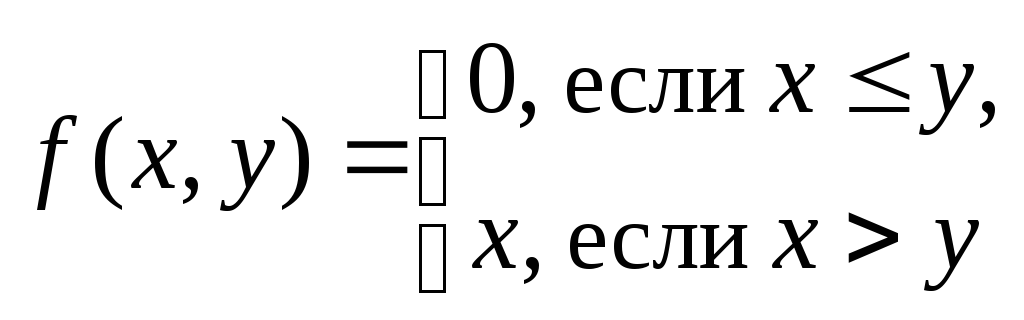
в СДНФ и в виде полинома Жегалкина.

Решение. Составим таблицу значений функции:

Табл. 1.13

0	0	0
0	1	0
0	2	0
1	0	1
1	1	0
1	2	0
2	0	2
2	1	2
2	2	0

Рассматривая только те строки таблицы, где , получаем:

Полином Жегалкина имеет вид . Запишем это выражение в матричной форме:

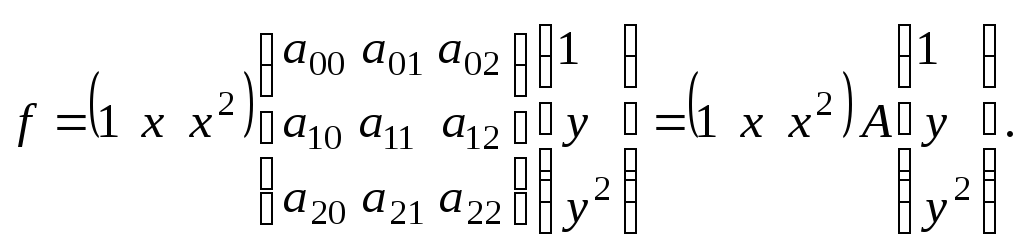
Подставляя значения и используя таблицу, получим:

.

Решая это матричное уравнение, будем иметь

.

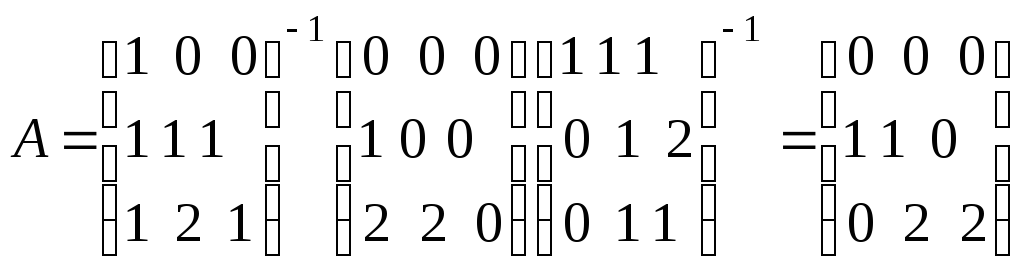Это означает, что

Задачи для самостоятельного решения

1. Представить функцию трёхзначной логики в виде полинома Жегалкина.

2. Представить функцию