§1.3. Реализация булевых функций формулами

Функция называетсясуперпозициейбулевых функций, если она получается некоторой подстановкой этих булевых функций друг в друга. Выражение, описывающее результат этой подстановки, называетсяформулой, задающей функцию.

Пусть и– две формулы. Говорят, что формулыиимеютодинаковое строение, если формуламожет быть получена из формулызаменой каждого функционального символана символ.

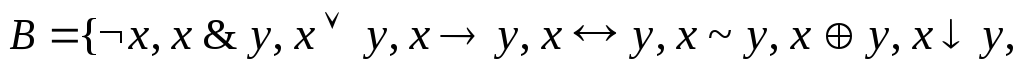
Пусть .Формулой над является всякое (и только такое) выражение вида:

(1) – любая переменная из множества

(2)

где иранее построенные формулы над.

Обычно принимаются следующие соглашения для сокращения записи формул над множеством связок :

а) внешние скобки у формул опускаются;

б) формула записывается в виде;

в) формула записывается в видеили;

г) считается, что связка сильнее любой двухместной связки из множества;

д) связка & считается сильнее любой другой двухместной связки из множества .

На множестве переменных введем функцию

.

О формуле , задающей функцию, говорят также, что формулареализует функцию. Две формулыиэквивалентны(), если реализуемые ими функциииравны.

В эквивалентности формул часто можно убедиться, построив таблицы соответствующих им функций.

Пример.Построив таблицы функций, выяснить эквивалентны ли формулы

и .

Решение.Построим векторы значений функцийи.

Табл. 1.7

0	0	0	1	0	0	0	0	1	0
0	0	1	1	0	1	1	1	1	1
0	1	0	1	1	1	0	0	0	0
0	1	1	1	1	1	0	1	0	0
1	0	0	0	1	0	1	1	1	1
1	0	1	0	1	1	0	0	1	0
1	1	0	0	1	1	0	1	0	0
1	1	1	0	1	1	0	0	0	0

Из таблицы 1.7 видно, что . Следовательно, формулыиэквиваленты.

Основные свойства элементарных функций

1. Коммутативность: , где.

2. Ассоциативность: , где.

3. Дистрибутивность

,

,

.

4. Законы де Моргана:

а) ; б).

5. Закон двойного отрицания .

Для упрощения формул часто используются тождества:

6. Законы поглощения: а) ; б).

7. а) ;

б) ;

в) ;

г) ;

д) .

8. а) ; б).

9. а) (склеивание);

б) (обобщенное склеивание); и т.д.

Для проверки всех приведенных равенств достаточно воспользоваться таблицей истинности.

Функция называетсядвойственной к функции.

Табл. 1.8

0	0	0	1	1
0	0	1	0	0
0	1	0	1	0
0	1	1	0	0
1	0	0	1	1
1	0	1	1	0
1	1	0	1	1
1	1	1	0	0

Замечание.Таблица двойственной функции получается из таблицы функцииинвертированием столбца значений функции и его переворачиванием (см. табл. 1.8).

Из определения двойственности следует, что

,

т.е. функция является двойственной к(свойство взаимности).

Функция называетсясамодвойственной, если. Например, самодвойственными являются функциии.

Обозначим через все различные символы переменных, встречающихся в множествах.

Теорема. Если

, то

.

Доказательство.

.

Следствие.(Принцип двойственности.) Если формулареализует функцию, то формулареализует функцию. Эту формулу называютформулой, двойственнойк, и обозначают.