Задачи для самостоятельного решения

1. Построив таблицы соответствующих функций, выяснить, эквивалентны ли формулы и:

а) и;

б) и;

в) и;

г) и.

2. Построив таблицы соответствующих функций, убедиться в справедливости следующих равенств:

а) ;

б) ;

в) ;

г) ;

д) .

3. Используя свойства элементарных функций, доказать эквивалентность формул и:

а) и;

б) и;

в) и.

4. Найти пары двойственных функций и все самодвойственные функции в множестве:

а)

, ;

б).

5. Доказать, что является двойственной к:

а) ,;

б) ,;

в) и.

6. Функция называетсясимметрической, если, гдепроизвольная перестановка чисел. Определить число симметрических функций отпеременных.

Ответы

1. а), б), в), да;г)нет.4. а) пары двойственных:,,; самодвойственных функций нет; б),,,. 6.

§1.4. Специальные представления булевых функций Совершенная дизъюнктивная и совершенная конъюнктивная нормальные формы

Ведем обозначение

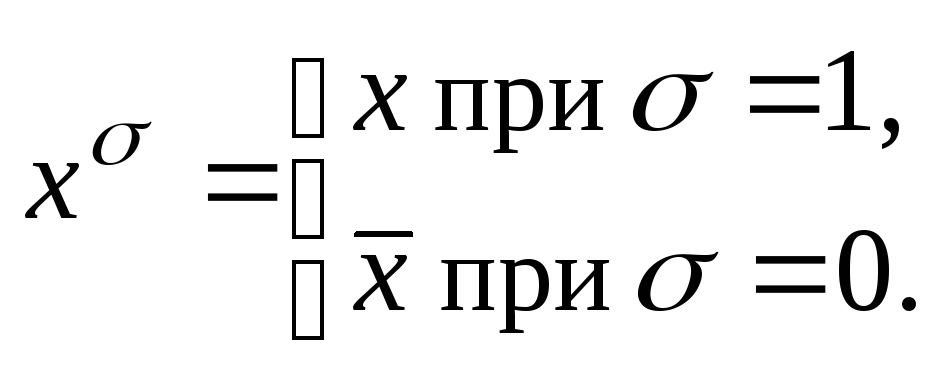
Выражение , гдекакой-либо двоичный набор, причем среди переменныхмогут быть совпадающие, называетсяэлементарной конъюнкцией. Выражения виданазываютбуквами. Число букв в элементарной конъюнкции называютрангомэлементарной конъюнкции.

Элементарная конъюнкция

– правильная, если в нее каждая переменная входит не более одного раза (включая и отрицание переменной);

– полная относительно переменных, если в нее каждая переменная (или ее отрицание) входит ровно один раз;

– монотонная, если она не содержит отрицаний переменных.

Формула вида , гдепопарно различные элементарные конъюнкции, называетсядизъюнктивной нормальной формой(сокращенно ДНФ). Числоназывается длиной ДНФ.

Теорема.Каждую булеву функциюпри любом() можно представить в виде

(*)

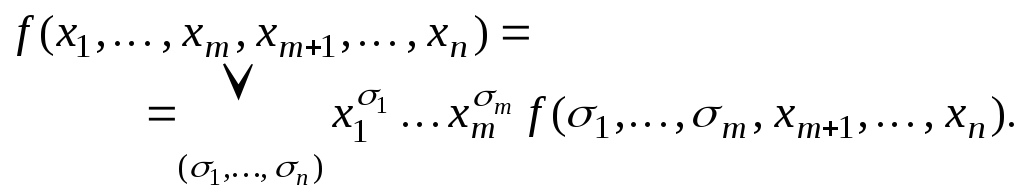Это представление называется разложением функции по переменным.

Доказательство.Заметим, чтоДалее рассмотрим произвольный набори покажем, что левая и правая часть формулы () принимают на нем одно и то же значение.

Левая часть дает , а правая

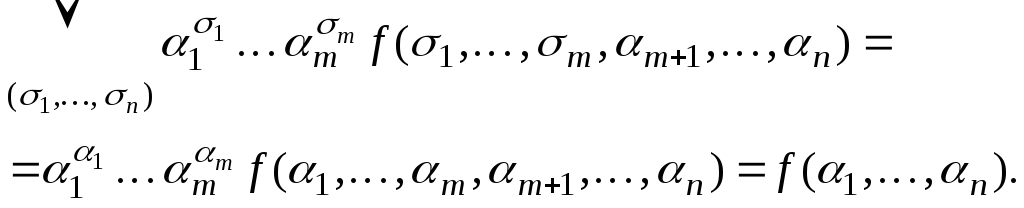
Следствие 1.Разложение по переменной . Пусть. Тогда

Следствие 2.Разложение по всем переменным. Пусть. Тогда

При получаем выражение

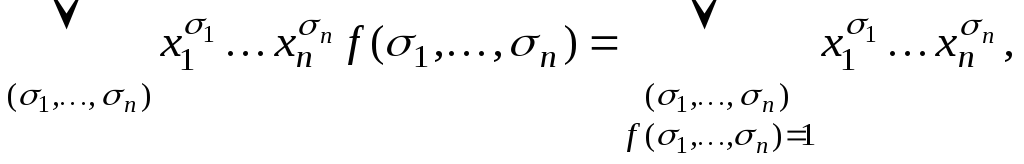
т.е.

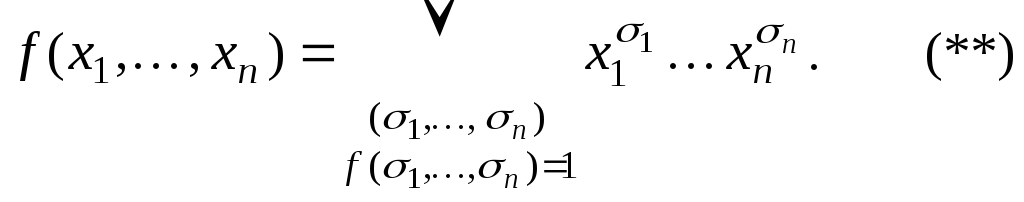
Разложение (**) носит название совершенной дизъюнктивной нормальной формы(СДНФ).

Замечания 1.Поскольку существует взаимно однозначное соответствие между таблицей истинностии СДНФ функции, то СДНФ функции единственна.

2.Единственная функция, не имеющая СДНФ, – константа 0.

3.Длина СДНФ функцииравна числу наборов, на которых функция принимает значение, равное 1.

Пример.Построить СДНФ функций:

а) ;

б) .

Табл. 1.9

0	0	1
0	1	1
1	0	0
1	1	1

Решение.а) Из таблицы 1.9 получаем, чтона наборах. Поэтому

_{Табл. 1.10}

0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	0
1	0	0	1
1	0	1	0
1	1	0	0
1	1	1	0

б) Из таблицы истинности заданной функции (табл. 1.10) видим, что значение функции равно 1 только на двух наборах. СДНФ функции имеет вид

Замечание.По данной ДНФ функцииможно построить ее СДНФ. Для этого достаточно «пополнить» каждую конъюнкцию недостающими буквами, применяя соотношение, а затем устранить повторения, применив эквивалентность.

Теорема.Каждая функция алгебры логики может быть выражена в виде отрицания, конъюнкции и дизъюнкции.

Доказательство. Пусть, тогда.

Если , то выразим ее в виде СДНФ

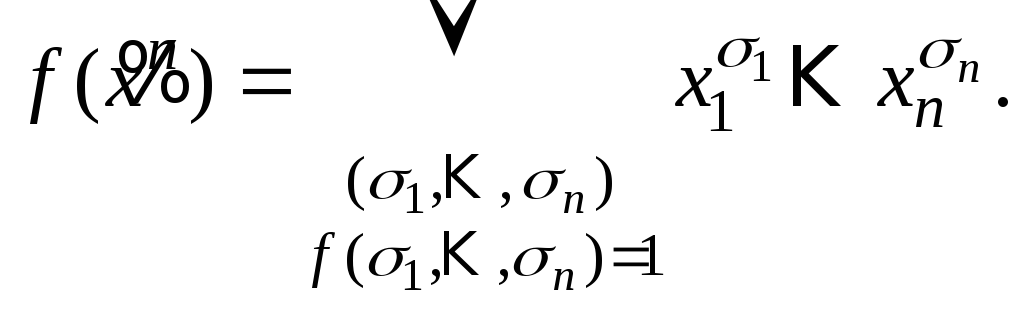
Следовательно, в обоих случаях функция выражается в виде формулы через отрицание, конъюнкцию и дизъюнкцию.

Выражение , гдекакой-либо двоичный набор, причем среди переменныхмогут быть совпадающие, называетсяэлементарной дизъюнкцией.

Элементарная дизъюнкция

– правильная, если в нее каждая переменная входит не более одного раза (включая и отрицание переменной);

– полная относительно переменных, если в нее каждая переменная (или ее отрицание) входит ровно один раз.

Формула вида , гдепопарно различные элементарные дизъюнкции, называетсяконъюнктивной нормальной формой(сокращенно КНФ). ЧислоназываетсядлинойКНФ.

В соответствии с принципом двойственности для функции можно получить следующее выражение для :

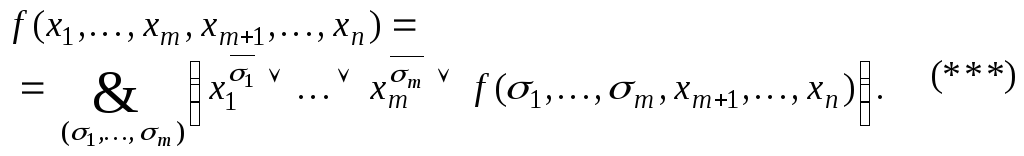
Для доказательства этого рассмотрим функцию, двойственную к функции . В соответствии с формулой (*) для нее получим:

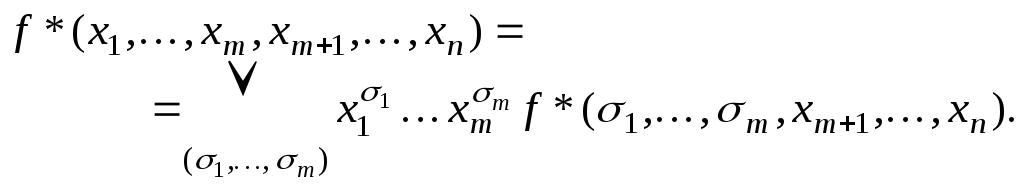
Из тождества для двойственных формул получим

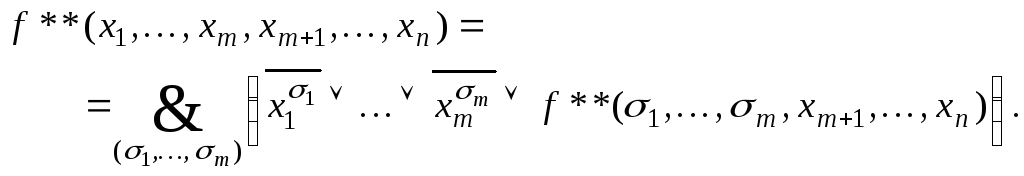Поскольку и, то получаем формулу (***).

Для иполучаем выражение

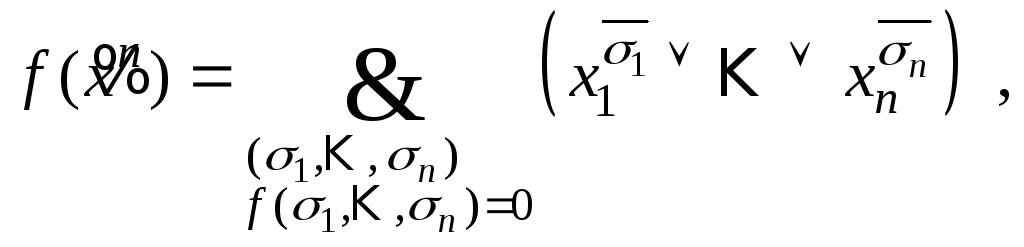
которое носит название совершенной конъюнктивной нормальной формы (СКНФ).

Замечания: 1.СКНФ функции единственна.

2.Единственная функция, не имеющая СКНФ, – константа 1.

3.Длина СКНФ функцииравна числу наборов, на которых функция принимает значение, равное 0.

Пример.Построить СДНФ функции.

Решение.Исходя из таблицы 1.9, получим, чтона одном наборе. Поэтому

Замечание.По данной КНФ функцииможно построить СКНФ функции. Для этого достаточно «пополнить» каждую из дизъюнкций недостающими буквами, применяя соотношение, а затем устранить повторения с помощью эквивалентности.