
- •§1.5. Полнота, замкнутость. Теорема Поста о полноте
- •Важнейшие замкнутые классы
- •Задачи для самостоятельного решения.
- •§1.6. Дизъюнктивные нормальные формы
- •Процедура упрощения д. Н. Ф. (алгоритм Блейка)
- •Алгоритм получения тупиковой д. Н. Ф.
- •Геометрическая интерпретация
- •Сокращенная д. Н. Ф.
- •Аналитические методы построения сокращенной д. Н. Ф. Метод Нельсона
- •Метод Квайна
- •Задачи для самостоятельного решения
Задачи для самостоятельного решения.
1. Перечислить все самодвойственные функции от двух переменных.
2.
Выяснить, является ли самодвойственной
функция
![]() :
:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
3.
Выяснить, является ли самодвойственной
функция
![]() ,
заданная векторно:
,
заданная векторно:
а)
![]() ;
б)
;
б)![]() ;
;
в)
![]() ;
;
г)
![]() .
.
4.
Определить, какие из переменных функций
![]() следует заменить на
следует заменить на![]() ,
а какие на
,
а какие на![]() с тем, чтобы получить константу:
с тем, чтобы получить константу:
а)
![]() ;
б)
;
б)![]() ;
;
в)
![]() ; г)
; г)![]() .
.
5.
Выяснить при каких
![]() функция
функция![]() :
:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
6. Перечислить все линейные функции от двух переменных.
7.
Представив функцию
![]() полиномом, выяснить, является ли она
линейной:
полиномом, выяснить, является ли она
линейной:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
8.
Выяснить, является ли линейной функция
![]() ,
заданная векторно:
,
заданная векторно:
а)
![]() ;
б)
;
б)![]() ;
;
в)
![]() ; г)
; г)![]() .
.
9.
Подставляя на места переменных нелинейной
функции
![]() функции из множества
функции из множества![]() ,
получить хотя бы одну из функций
,
получить хотя бы одну из функций![]() :
:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
10.
Найти число линейных функций
![]() ,
,
а)
существенно зависящих в точности от
![]() переменных;
переменных;
б)
удовлетворяющих условию
![]() .
.
11.
Выяснить, принадлежит множеству
![]() функция
функция![]() :
:
а)
![]() ;
;
б)
![]() .
.
12.
Выяснить, при каких
![]() функция
функция![]() :
:
а)
![]() ;
;
б)
![]() .
.
13. Приведите все монотонные функции от двух переменных.
14.
Выяснить, является ли монотонной функция
![]() :
:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
15.
Выяснить, является ли монотонной функция
![]() ,
заданная векторно:
,
заданная векторно:
а)
![]() ;
б)
;
б)![]() ;
;
в)
![]() ; г)
; г)![]() .
.
16.
Для немонотонной функции
![]() указать два соседних набора
указать два соседних набора![]() и
и![]() значений переменных таких, что
значений переменных таких, что![]() и
и![]() :
:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
17.
Выяснить при каких
![]() функция
функция![]() монотонна:
монотонна:
а)
![]() ; б)
; б)![]() .
.
18.
Подсчитать число функций, зависящих от
переменных
![]() и принадлежащих множеству
и принадлежащих множеству![]() :
:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
;
г)
![]() ; д)
; д)![]() ;
е)
;
е)![]() .
.
19.
Выяснить, полна ли система функций
![]() :
:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
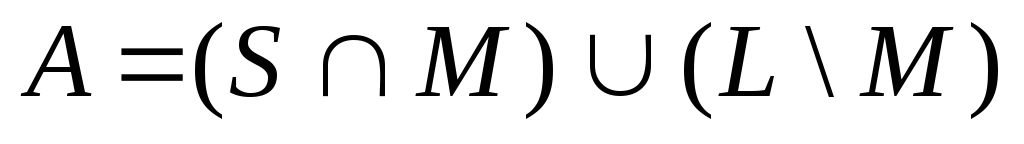 ;
;
е)
![]() .
.
Ответы
1.![]() .2. а)
.2. а)![]() ;б)
;б)![]() ;в)
;в)![]() .3. а)
.3. а)![]() ;
;
б)![]() ;в)
;в)![]() ;г)
;г)![]() .4. а)
.4. а)![]() заменить на
заменить на![]() ,
,![]() на
на![]() или наоборот;б)существуют две пары наборов таких, что
или наоборот;б)существуют две пары наборов таких, что![]() :
(010) – (101) и (011) – (100). В первом случае
заменив
:
(010) – (101) и (011) – (100). В первом случае
заменив![]() на
на![]() ,
а
,
а![]() на
на![]() получим константу 0; во втором заменив
получим константу 0; во втором заменив![]() на
на![]() ,
а
,
а![]() на
на![]() получим константу 1;в)получим константу 1, заменив, например,
получим константу 1;в)получим константу 1, заменив, например,![]() на
на![]() ,
а
,
а![]() на
на![]() получим константу 0; во втором заменив
получим константу 0; во втором заменив![]() на
на![]() ,
а
,
а![]() на
на![]() ;г)существуют
три пары наборов таких, что
;г)существуют
три пары наборов таких, что![]() :
(0011) – (1100), (0100) – (1011) и (0110) – (1110). Можем
координаты, соответствующие 0 в первом
наборе каждой пары заменить на
:
(0011) – (1100), (0100) – (1011) и (0110) – (1110). Можем
координаты, соответствующие 0 в первом
наборе каждой пары заменить на![]() ,
а соответствующие 1 – на
,
а соответствующие 1 – на![]() .5. а)при
нечетных
.5. а)при
нечетных![]() ;б) –в)при всех
;б) –в)при всех![]()
![]() .6.
.6.![]() .7. а)
.7. а)![]()
![]()
![]() ;б)
;б) ![]() ;в)
;в) ![]() .8.а)
.8.а) ![]() ;б)
;б) ![]() ;в)
;в) ![]() ;г)
;г) ![]() .9. а)
.9. а)![]() ;б)
;б)![]() ;в)
;в)![]() ;
;
г)![]() .10. а)
.10. а)![]() б)
б)![]() .11. а)
.11. а)![]() ;
;
б)
![]() .12. а)при
нечетных
.12. а)при
нечетных![]() ;б) при всех
;б) при всех![]() и
и![]()
![]() .13.
.13.![]() .14. а)
.14. а)![]() ;б)
;б)![]() ;в)
;в)![]() ;г)
;г)![]() .15. а)
.15. а)![]() ;б)
;б)![]() ;в)
;в)![]() ;г)
;г)![]() .16. а)
.16. а)![]() ,
,![]() ;б)
;б)![]() ,
,![]() или
или![]() ;
;![]() ,
,![]() или
или![]() ;
;
в)
![]() ,
,![]() .
.
17.
а)при![]()
![]() ,
при
,
при![]()
![]() б) при
б) при![]() и
и![]() при
всех
при
всех![]() .
.![]() .18. а)
.18. а)![]() ;б)
;б)![]() ;в)
;в)![]() ;г)
;г)![]() ;д)
;д)![]() ;е)
;е)![]() .19. а)Нет.
.19. а)Нет.![]() .б)Нет.
.б)Нет.![]() .в)Нет.
.в)Нет.![]() .г)Да.д)Да.е)Нет.
.г)Да.д)Да.е)Нет.![]() .
.
§1.6. Дизъюнктивные нормальные формы
Пример.Рассмотрим функцию![]() .
Приведем несколько различных формул,
являющихся д. н. ф. и реализующих функцию
.
Приведем несколько различных формул,
являющихся д. н. ф. и реализующих функцию![]() .
Это ее СДНФ =
.
Это ее СДНФ =![]() и д. н. ф.:
и д. н. ф.:![]() ,
,![]() ,
,![]() .
Заметим, что
.
Заметим, что![]() .
.
Лемма.Число различных д. н. ф. от переменных![]() равно
равно![]() .
.
Доказательство.Действительно, число различных
элементарных конъюнкций![]() равно
равно![]() (“пустой”
конъюнкции сопоставлена константа 1),
так как для каждой переменной
(“пустой”
конъюнкции сопоставлена константа 1),
так как для каждой переменной![]() имеется три возможности: присутствует
в конъюнкции, присутствует с отрицанием
и отсутствует. Выпишем все элементарные
конъюнкции, поставив между ними
дизъюнкции:
имеется три возможности: присутствует
в конъюнкции, присутствует с отрицанием
и отсутствует. Выпишем все элементарные
конъюнкции, поставив между ними
дизъюнкции:![]() .
Удаляя различные
.
Удаляя различные![]() ,
получим все возможные д. н. ф. Следовательно,
число различных д. н. ф. равно
,
получим все возможные д. н. ф. Следовательно,
число различных д. н. ф. равно![]() и одной функции соответствует несколько
различных д. н. ф.
и одной функции соответствует несколько
различных д. н. ф.
Введем
функционал
![]() ,
означающийсложностьд. н. ф.,
обладающий свойствами:
,
означающийсложностьд. н. ф.,
обладающий свойствами:
1.
![]() .
.
2. Если
![]() ,
то
,
то![]() .
.
3. Если
![]() и
и![]() ,
то
,
то![]() .
.
4. Если
![]() и
и![]() получены одна из другой переименованием
переменных, то
получены одна из другой переименованием
переменных, то![]() .
.
Примеры:
1)![]() – число букв в д. н. ф.; 2)
– число букв в д. н. ф.; 2)![]() – число элементарных конъюнкций; 3)
– число элементарных конъюнкций; 3)![]() – число знаков отрицаний.
– число знаков отрицаний.
Тогда для рассмотренного в начале параграфа примера:
![]() ,
,
![]() ,
,![]() ;
;
![]() ,
,
![]() ;
;
![]() ,
,
![]() ,
,![]() .
.
Д.
н. ф.
![]() называетсяминимальнойдля
данной функции
называетсяминимальнойдля
данной функции![]() ,
если
,
если![]() имеет минимальное значение.
имеет минимальное значение.
Проблема
минимизации д. н. ф. состоит в том, чтобы
для произвольной функции
![]() построить минимальную д. н. ф. Конечно,
существует алгоритм, реализующий
проблему минимизации, – это алгоритм
полного перебора. Однако, этот алгоритм
занимает слишком много времени, и для
функций, зависящих от большого числа
переменных, реализован быть не может.
В связи с этим важное значение приобретают
методы, позволяющие за реальное время
получить д. н. ф., в той или иной степени
приближенные к минимальной.
построить минимальную д. н. ф. Конечно,
существует алгоритм, реализующий
проблему минимизации, – это алгоритм
полного перебора. Однако, этот алгоритм
занимает слишком много времени, и для
функций, зависящих от большого числа
переменных, реализован быть не может.
В связи с этим важное значение приобретают
методы, позволяющие за реальное время
получить д. н. ф., в той или иной степени
приближенные к минимальной.
