Р Рис. 2.41ешение типовых задач

1.Существует ли Эйлеров цикл у графа, изображенного на рис. 2.41? Если существует, построить его.

Решение.Так как степени всех вершин четны, тот эйлеров цикл существует. Возьмем произвольный цикл, например, (1, 5, 3, 1). Этот цикл не содержит все ребра графа. Рассмотрим граф, полученный из исходного удалением этого цикла. Удаленный граф и оставшийся, в силу связности исходного графа всегда имеют общую вершину, в данном случае – 5. Рассмотрим теперь произвольный цикл нового графа, начинающийся в вершине 5, например, (5, 4, 6, 5). Присоединим его к первому циклу: (1, 5, 4, 6, 5, 3, 1). Остается единственный цикл (4, 1, 2, 4), присоединив который, получим эйлеров цикл (1, 5, 4, 1, 2, 4, 6, 5, 3, 1).

2.Найти число компонент связности леса, который имеет 40 вершин и 23 ребра.

Решение. Так как для леса, получаем,.

3. Чему может равняться число ребер графа, имеющего 20 вершин и 4 компоненты связности?

Решение. Так как, имеем, следовательно,. Покажем, что найдется граф, для которого,,. Пусть 3 компоненты связности – изолированные вершины, четвертая – простая цепьС₁₇с 16 ребрами. Таким образом, минимальное число ребер равно 16. Выясним, каким может быть максимальное число ребер.

Докажем, что наибольшее количество ребер у графа, три компоненты связности которого представляют собой изолированные вершины, четвертая – полны граф К₁₇с числом ребер, равным 136. Действительно, рассмотрим граф с 20 вершинами и 4 компонентами связности, из которых по крайней мере 2 содержат не менее двух вершин. Предположим, что. Возьмем произвольно вершину из, удалим все ребра, инцидентные ей, и соединим ее ребрами со всеми вершинами из. Новый граф будет иметь то же количество вершин и компонент связности, но больше ребер. Таким образом, количество ребер может быть от 16 до 136.

4. Чему может равняться число компонент связности графа, имеющего 12 вершин и 27 ребер?

Решение. Так как простая цепьС₁₂имеет 11 ребер, а полный графК₁₂– 66 ребер, то существует связный граф, имеющий 12 вершин и 27 ребер. Минимальное число компонент связности равно 1. Для того, чтобы определить максимально возможное число компонент связности, найдем наименьший полный граф, число ребер которого не меньше 27:. Рассмотрим граф, 4 компоненты связности представляют собой изолированные вершины, а пятая имеет 8 вершин и 27 ребер. Докажем, что 6 компонент связности быть уже не может. Действительно, по предыдущей задаче, граф, имеющий 12 вершин и 6 компонент связности, может иметь не более 21 ребра. Таким образом Таким образом, количество компонент связности может быть от 1 до 5.

5

а) б)

Рис. 2.42

.Для графа, изображенного на рис.2.42(а) найти цикломатическое число, укзать базис циклов, построить остовное дерево.

Для данного графа , , . Следовательно,и изнадо удалить три ребра, чтобы получилось дерево. Базис циклов также состоит из трех циклов. Выберем произвольно цикл, например,. Удалим из графа реброе₂. В получившемся графе возьмем цикл. Удалим из графа реброе₅. В получившемся графе возьмем цикл . Удалим из графа реброе₁₀. Получим остовное дерево графа, изображенное на рис. 2.42б). ЦиклыС₁,С₂,С₃образуют базис. Разложим какой-нибудь цикл, например,, по этому базису. Запишем коды циклов:

Так как были удалены ребра е₂,е₅,е₁₀, то в матрице, составленной из кодов цикловС₁,С₂,С₃,С₄, базисным будет минор, составленный из столбцов под номерами 2, 5, 10:.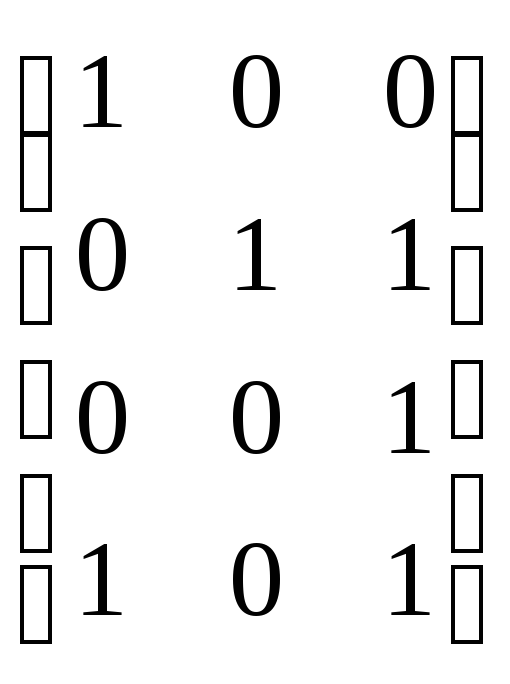

Отсюда получаем .