
Д Рис. 2.31еревья
Связный граф без циклов называется деревом. Любой граф без циклов называетсяациклическим(илилесом). Таким образом, компонентами связности леса являются деревья. На рис. 2.31 изображен лес, каждая компонента связности его является деревом.
Теорема.
Связный граф является деревом тогда и
только тогда, когда число его вершин на
единицу больше числа его ребер, т.е.
![]() .
.
Доказательство.Необходимость.Заметим, что если
графG– дерево, то он имеет хотя бы
одну вершину степени 1 (висячую вершину).
Действительно, предположим, что все
вершины имеют степень, не меньшую 2.
Возьмем произвольную вершину, обозначим
ее![]() .
Из нее выходит по крайней мере два ребра.
Найдется вершина
.
Из нее выходит по крайней мере два ребра.
Найдется вершина![]() такая,
что
такая,
что![]() .
Так как степень вершины
.
Так как степень вершины![]() не
меньше 2, то найдется вершина
не
меньше 2, то найдется вершина![]() ,
отличная от
,
отличная от![]() ,
такая, что
,
такая, что![]() ,
и так далее. Так как число вершин конечно,
то в этой последовательности вершин
найдутся совпадающие, и мы получим цикл,
что противоречит определению дерева.
Следовательно, висячая вершина существует.
,
и так далее. Так как число вершин конечно,
то в этой последовательности вершин
найдутся совпадающие, и мы получим цикл,
что противоречит определению дерева.
Следовательно, висячая вершина существует.
Далее
доказательство проведем индукцией по
числу вершин п. Прип = 1 число
ребер равно 0 и утверждение верно.
Предположим оно верно при любом количестве
вершин, меньшемп. Рассмотрим графGспвершинами. Среди них есть
висячая. Рассмотрим подграфG',
порожденный множеством остальных
вершин. Для него по индукционному
предположению![]() .
Кроме того,
.
Кроме того,![]() .
Следовательно,
.
Следовательно,![]() .
Необходимость доказана.
.
Необходимость доказана.
Достаточность.Пусть для связного графаGвыполняется
условие![]() .
Для того, чтобы доказать, чтоGявляется деревом, нужно показать лишь
отсутствие циклов. Предположим, что
циклы есть, тогда удаление одного ребраеиз цикла не нарушает связности,
граф
.
Для того, чтобы доказать, чтоGявляется деревом, нужно показать лишь
отсутствие циклов. Предположим, что
циклы есть, тогда удаление одного ребраеиз цикла не нарушает связности,
граф![]() тоже связный. Следовательно, для него
выполняется неравенство
тоже связный. Следовательно, для него
выполняется неравенство![]() .
Но
.
Но![]() ,
следовательно,
,
следовательно,![]() и значит,
и значит,![]() ,
что противоречит условию. Следовательно,Gявляется связным графом без циклов,
т.е. деревом. Теорема доказана.
,
что противоречит условию. Следовательно,Gявляется связным графом без циклов,
т.е. деревом. Теорема доказана.
Свойства деревьев.
Любые две вершины дерева можно соединить путем. Если это простой путь, то он единственный.
Если для некоторого дерева GV(G)2, то оно имеет не менее двух висячих вершин.
Кодировка дерева
С
Рис. 2.32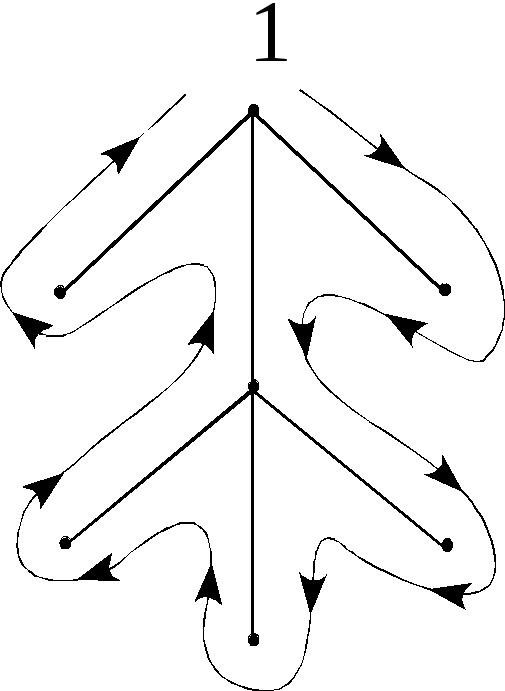
П
c C
![]() .
Поставим в соответствие деревуТспребрами слово, состоящее из 0 и 1
длиной 2пследующим образом. Выберем
произвольно вершину и начнем обход
дерева по произвольному ребру так, чтобы
ребра все время оставались справа,
поворачивая в висячих вершинах. Если
ребро встретилось в первый раз, записываем
0, во второй – 1. Код дерева, представленного
на рис.2.32 – (010010101101) (обход начат с вершины
1).
.
Поставим в соответствие деревуТспребрами слово, состоящее из 0 и 1
длиной 2пследующим образом. Выберем
произвольно вершину и начнем обход
дерева по произвольному ребру так, чтобы
ребра все время оставались справа,
поворачивая в висячих вершинах. Если
ребро встретилось в первый раз, записываем
0, во второй – 1. Код дерева, представленного
на рис.2.32 – (010010101101) (обход начат с вершины
1).
З
а) б) в)
Рис. 2.33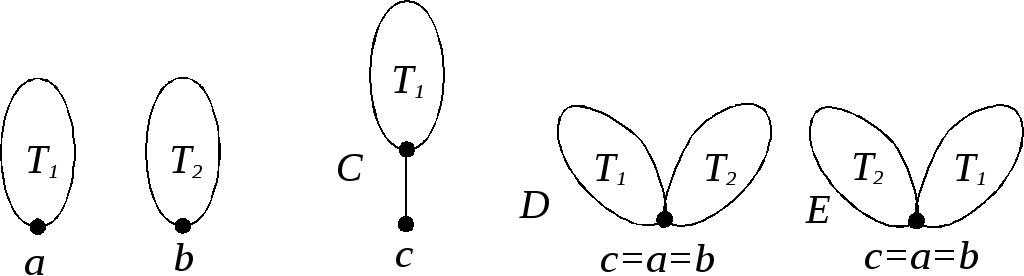
![]() и
и![]() соответственно, то деревуС(рис.
2.33, б) сопоставляется код (0
соответственно, то деревуС(рис.
2.33, б) сопоставляется код (0![]() 1),
а деревьямDиE (рис. 2.33, в) – коды
1),
а деревьямDиE (рис. 2.33, в) – коды![]() и
и![]() .
.
Не всякая последовательность из пединиц ипнулей служит кодом дерева. Необходимым и достаточным условием для этого служит следующее:в любом начальном отрезке последовательности количество нулей не меньше количества единиц.Если это условие выполняется, дерево может быть построено по коду.
